树的相关定义
- 结点:树中的一个独立单元,包含一个数据元素及若干指向其他子树的分支
- 结点的度: 结点拥有的子树数称为结点的度,例如A的度是3
- 树的度: 树内各节点度的最大值,实例中的度为3
- 叶子: 度为0的结点称为叶子或终端结点
- 非终端结点: 度不为0的结点称为非终端节点或分支结点,除了根节点以外,非终端节点也称为内部节点
- 双亲和孩子: 结点的子树的根称为该节点的孩子,该节点称为孩子的双亲
- 兄弟: 同一个双亲的孩子之间称为兄弟结点
- 祖先: 从根到该节点所经历的分支上的所有节点,如M的祖先为A D H
- 子孙: 以某结点为根的子树中的任一结点都成为该结点的子孙,如B的子孙为EF
- 层次: 结点地层次从根开始定义起,根为第一层,根的孩子为第二层,树中任一层次等于双亲结点的层次加1
- 堂兄弟: 双亲在同一层的结点互为堂兄弟,例如G与EFHIJ互为堂兄弟
- 有序树和无序树: 如果将树的结点的各子树看成从左到右是有次序的(不能互换)则称为有序树,否则是无序树
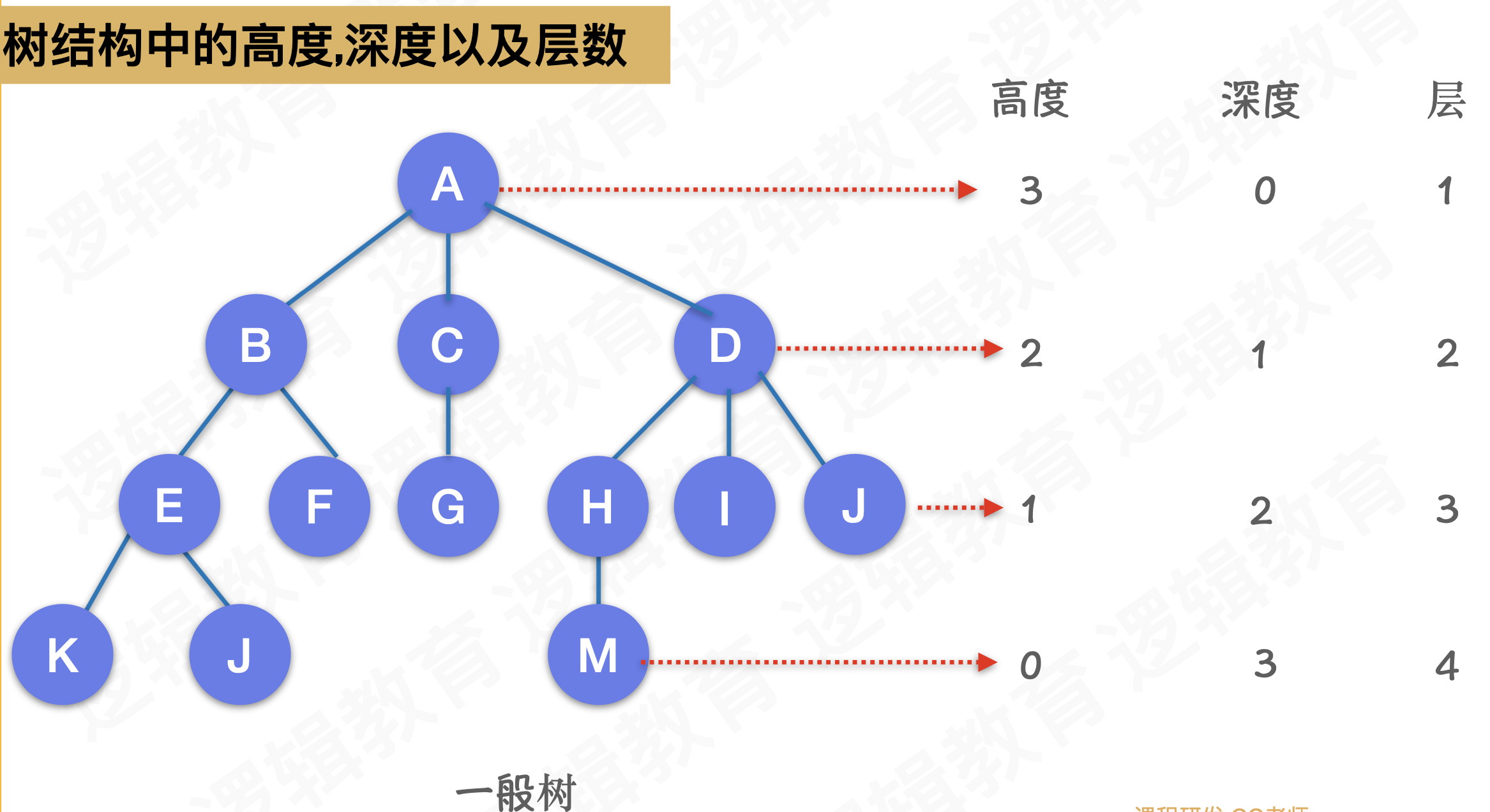
- 结点的高度: 结点到叶子结点的最长路径(边数)
- 结点的深度: 根节点到这个结点所经历的边的个数
- 节点的层数: 结点的深度-1
- 树的高度: 根节点的高度
二叉树相关定义
二叉树的五种形态
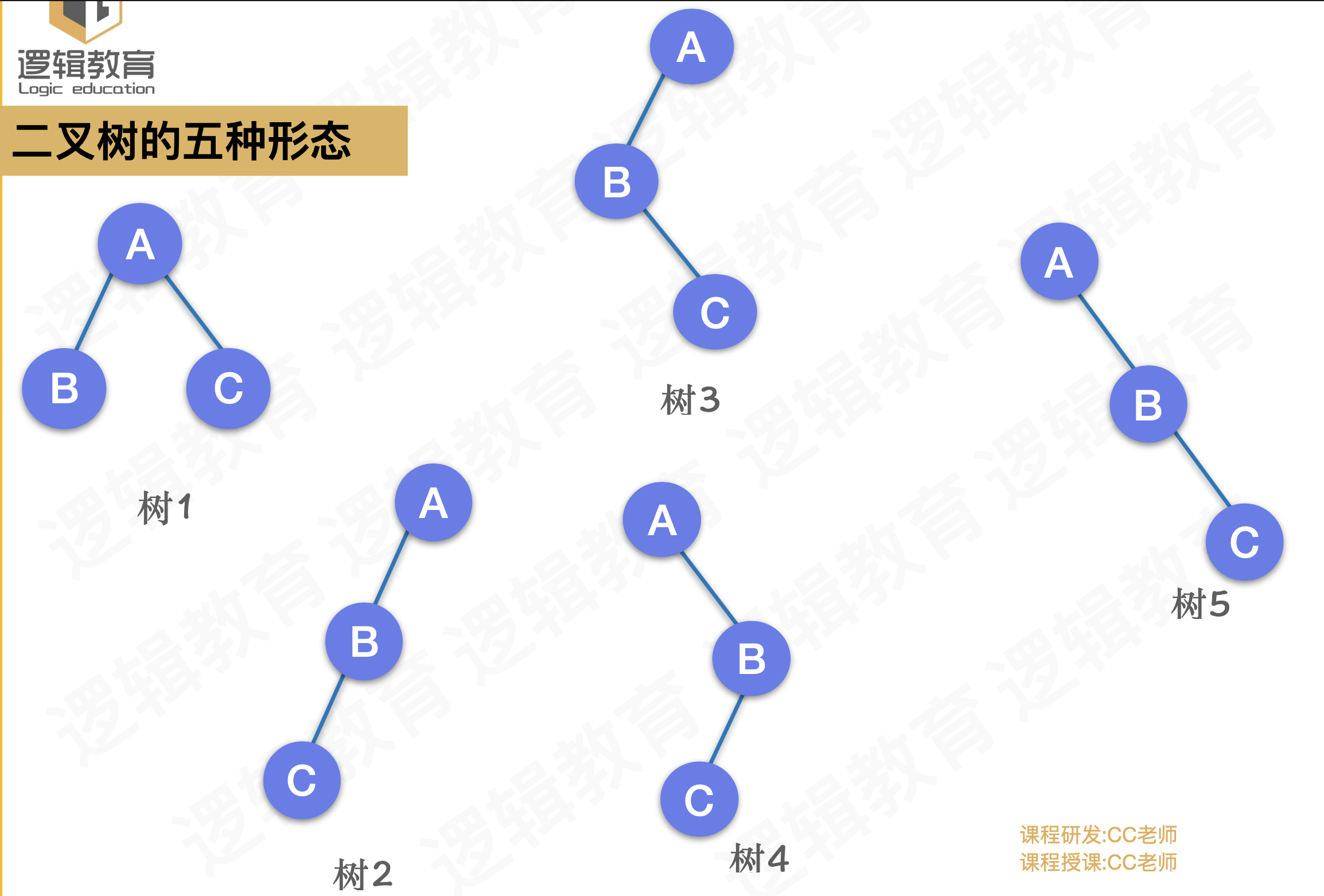
特殊的二叉树
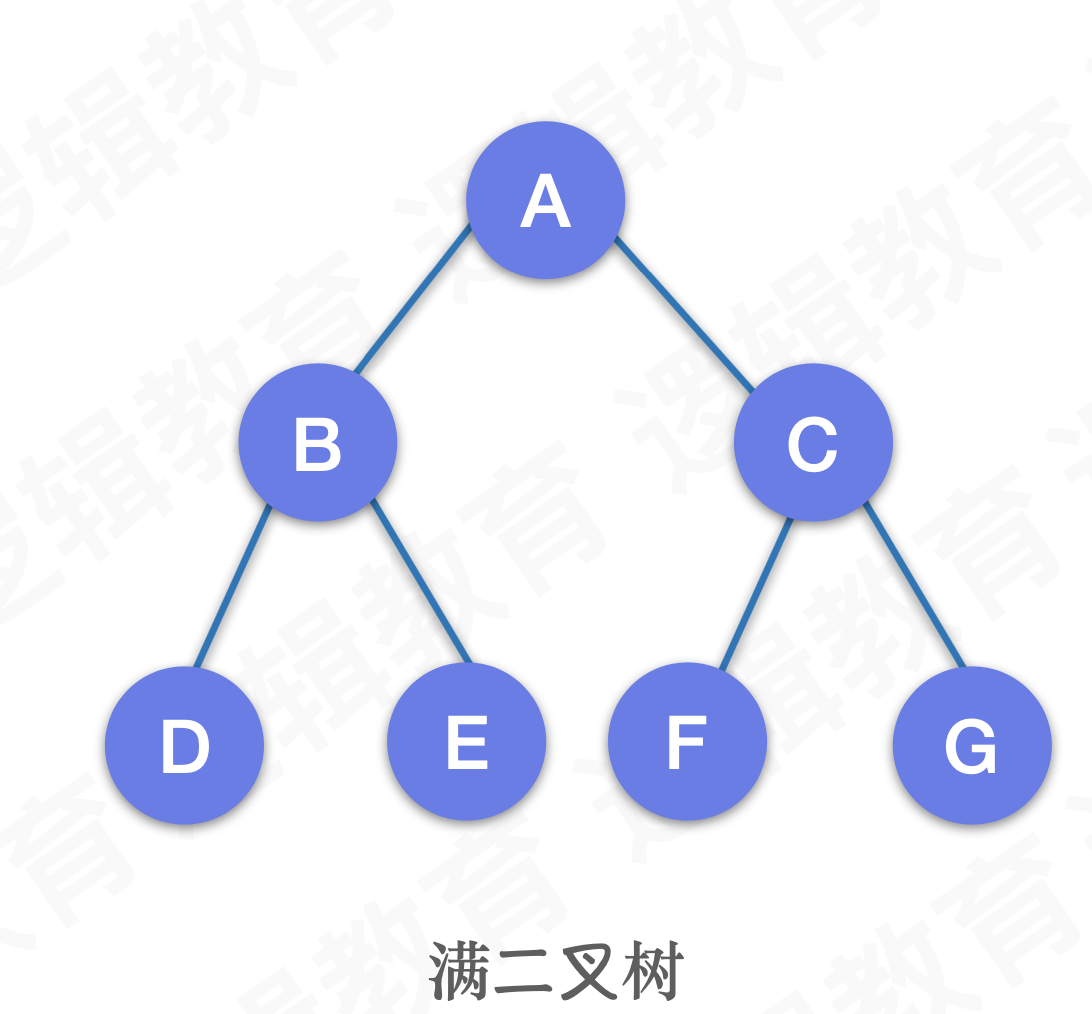
- 满二叉树
每个结点都有两个子节点
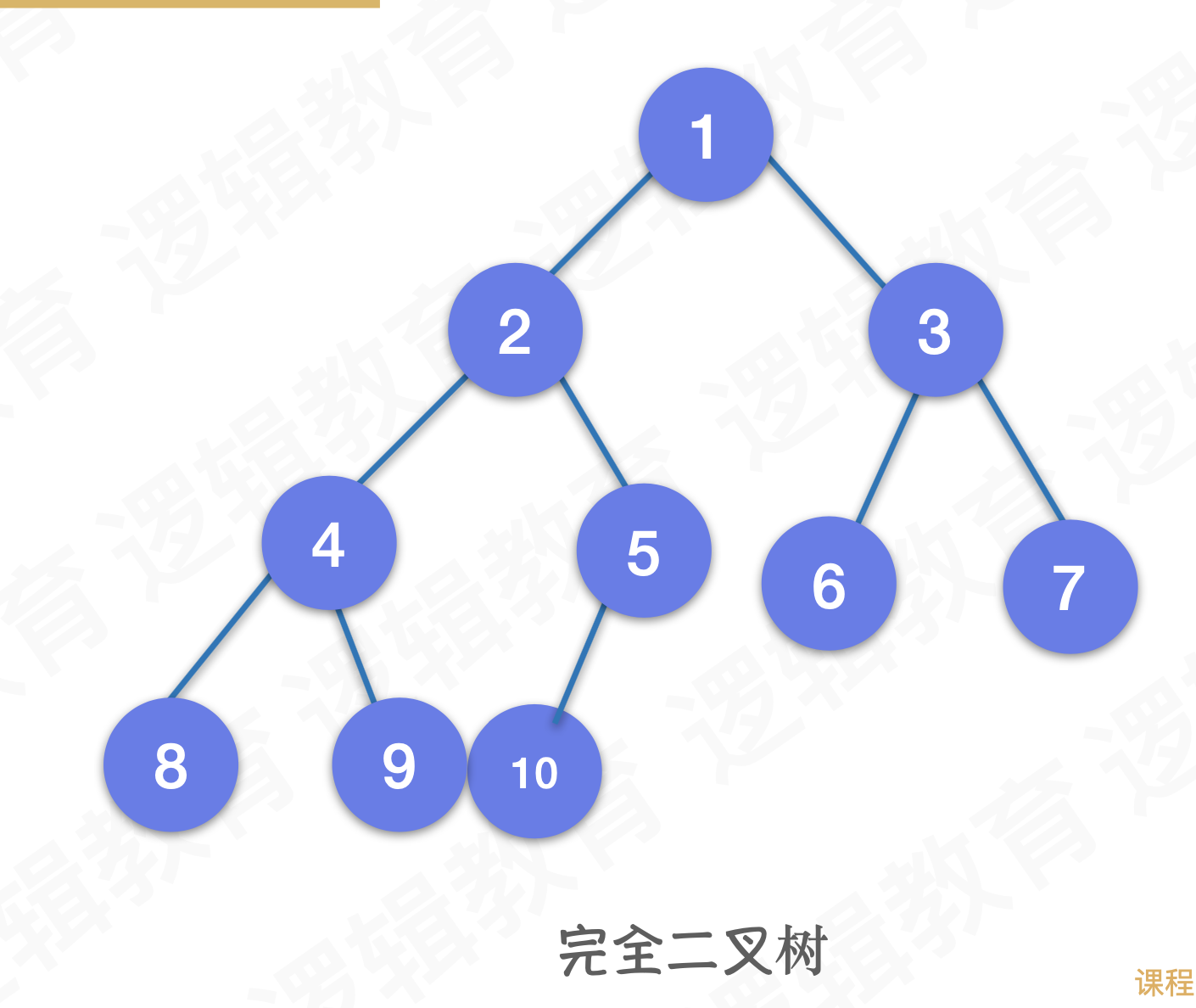
- 完全二叉树
完全二叉树就是按照满二叉树的样子,结点的序号没有确实的树
- 斜树

二叉树的性质
- 1.在二叉树的第i层上最多有2^(i-1)个结点
- 2.深度为k的二叉树最多有2^k-1个结点(k>=1)
- 3.对于任何一个二叉树T,如果其终端节点数为n0,度为2的结点数为n2,则n0 = n2+1
- 4.具有n个结点的完全二叉树深度为(log2(n))+1
- 5.对具有n个结点的完全二叉树,如果按照从上至下和从左至右的顺序对二叉树的所有节点从1开始编号,则对于任意的序号为i的结点有:
- A 如果i>1,那么序号为i的结点的双亲结点序号为i/2
- B 如果i=1,那么序号为i的结点为根节点,无双亲结点
- C 如果2i<=n,那么序号为i的结点的左孩子结点序号为2i
- D 如果2i>n,那么序号为i的结点无左孩子
- E 如果2i+1<=n,那么序号为i的结点右孩子序号为2i+1
- F 如果2i+1>n,那么序号为i的结点无右孩子
二叉树顺序存储的定义与相关操作的实现
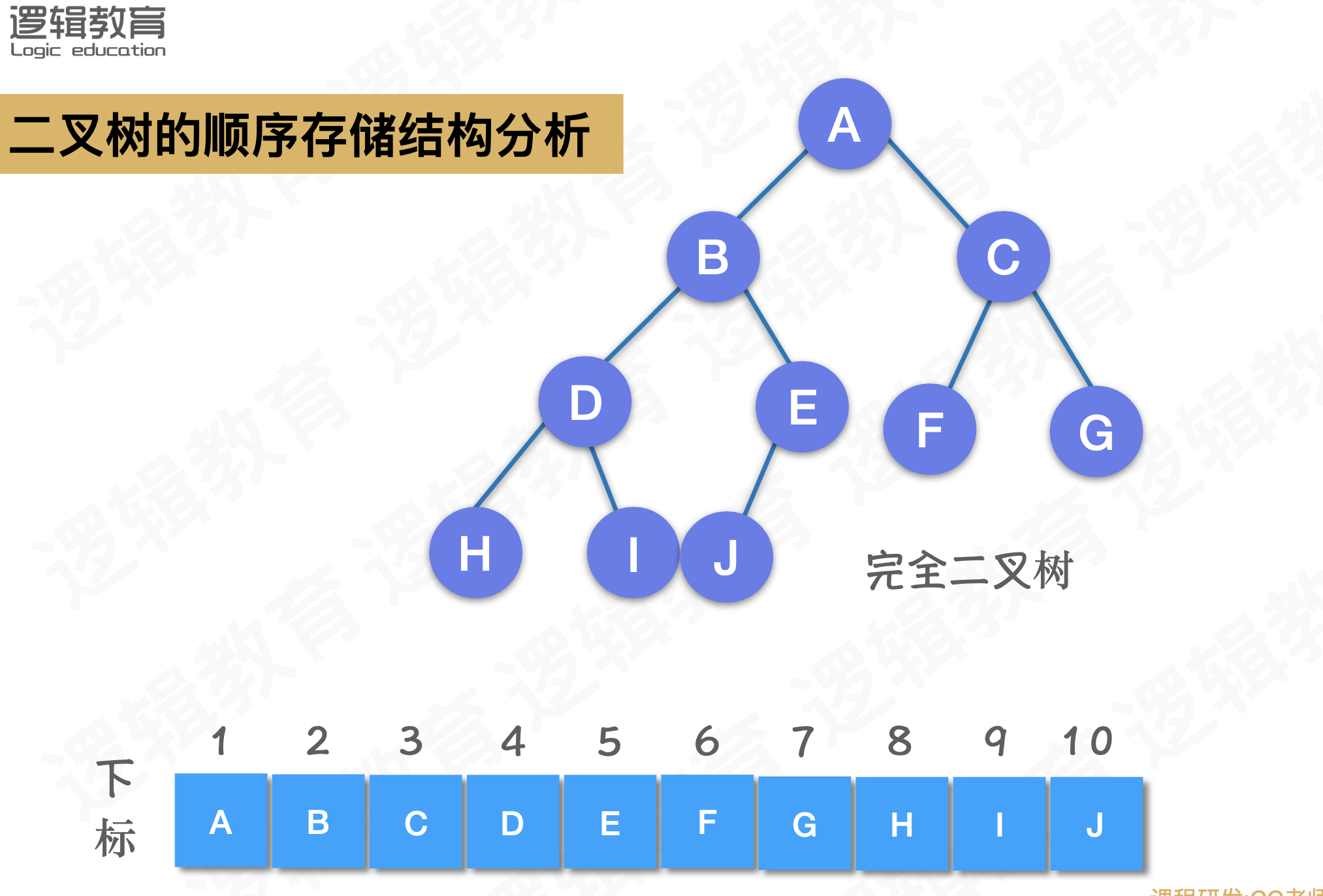
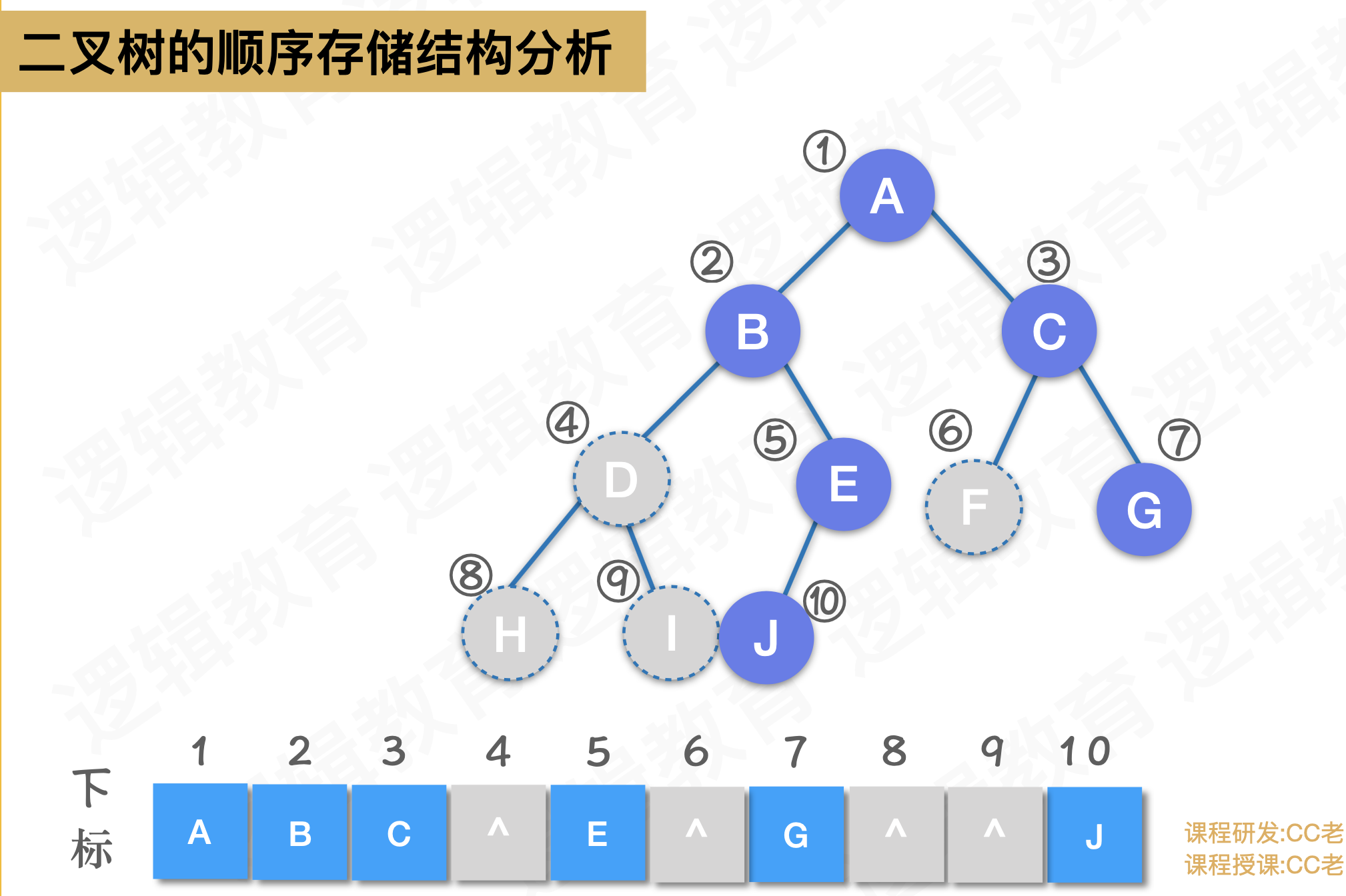
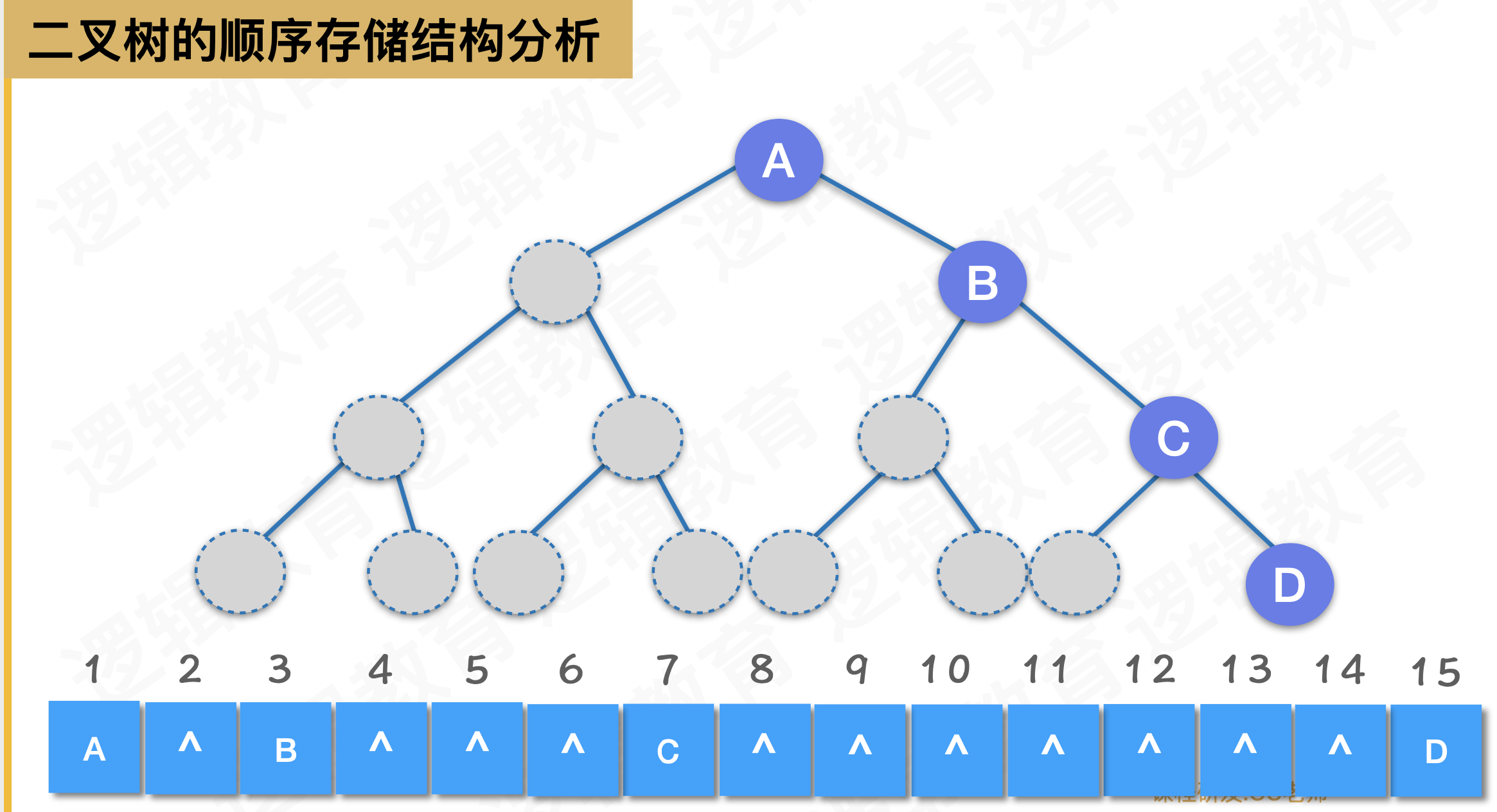
二叉树的实现
- 1 visit
- 2 构造空二叉树T,因为T是固定数组,不会改变
- 3 按层序次序输⼊二叉树中的结点值(字符型或整型),构造顺序存储的⼆叉树T
- 4 判断二叉树是否为空
- 5 获取二叉树的深度
- 6 返回处于位置e(层,本层序号)的结点值
- 7 获取⼆叉树跟结点的值
- 8 给处于位置e的结点赋值
- 9 获取e的双亲;
- 10 获取某个结点的左孩⼦
- 11 获取某个结点的右孩⼦
- 12 获取结点的左兄弟
- 13 获取结点的右兄弟
二叉树的顺序存储结构
typedef CElemType SqBiTree[MAX_TREE_SIZE];
CElemType Nil = 0; //0,65535
typedef struct{
int level;//结点层号
int order; //序号按照满二叉树的规则
}Position;
//初始化二叉树
Status InitBiTree(SqBiTree T){
for(int i=0;i<MAX_TREE_SIZE;i++){
T[i] = Nil;
}
return OK;
}
//创建二叉树
Status CreateBiTree(SqBiTree T){
int i =0;
while(i<10){
T[i] = i+1;
printf("%d",T[i]);
if(i!=0 && T[(i+1)/2-1] == Nil && T[i]!=Nil){
printf("出现了无双亲的非根节点%d\n",T[i]);
exit(ERROR);
}
i++;
}
while(i<MAX_TREE_SIZE){
T[i] = Nil;
i++;
}
return OK;
}
//清空二叉树
#define ClearBiTree InitBiTree
//二叉树判空
Status BiTreeEmpty(SqBiTree T){
if(T[0] == Nil)
return TRUE;
return FALSE;
}
//二叉树的深度
int BiTreeDepth(SqBiTree T){
int j = -1;
int i;
//找到最后一个结点
for(i = MAX_TREE_SIZE-1;i>=0;i-- ){
if(T[i] != Nil)
break;
}
do{
j++;
}while(powl(2,j)<=i);
return j;
}
//处于e位置上的结点的值
CElemType Value(SqBiTree T,Position e){
//level ->层
//order ->序号
printf("%d\n",(int)pow(2,e.level-1));
printf("%d\n",e.order);
return T[(int)pow(2,e.level-1)+e.order-2];
}
Status Assign(SqBiTree T,Position e,CElemType value){
int i=(int)pow(2,e.level-1)+e.order-2;
if(value != Nil && T[((i+1)/2)-1)] == Nil){
return ERROR;
}
T[i] = value;
return OK;
}
//获得结点的左孩子,右孩子,双亲结点
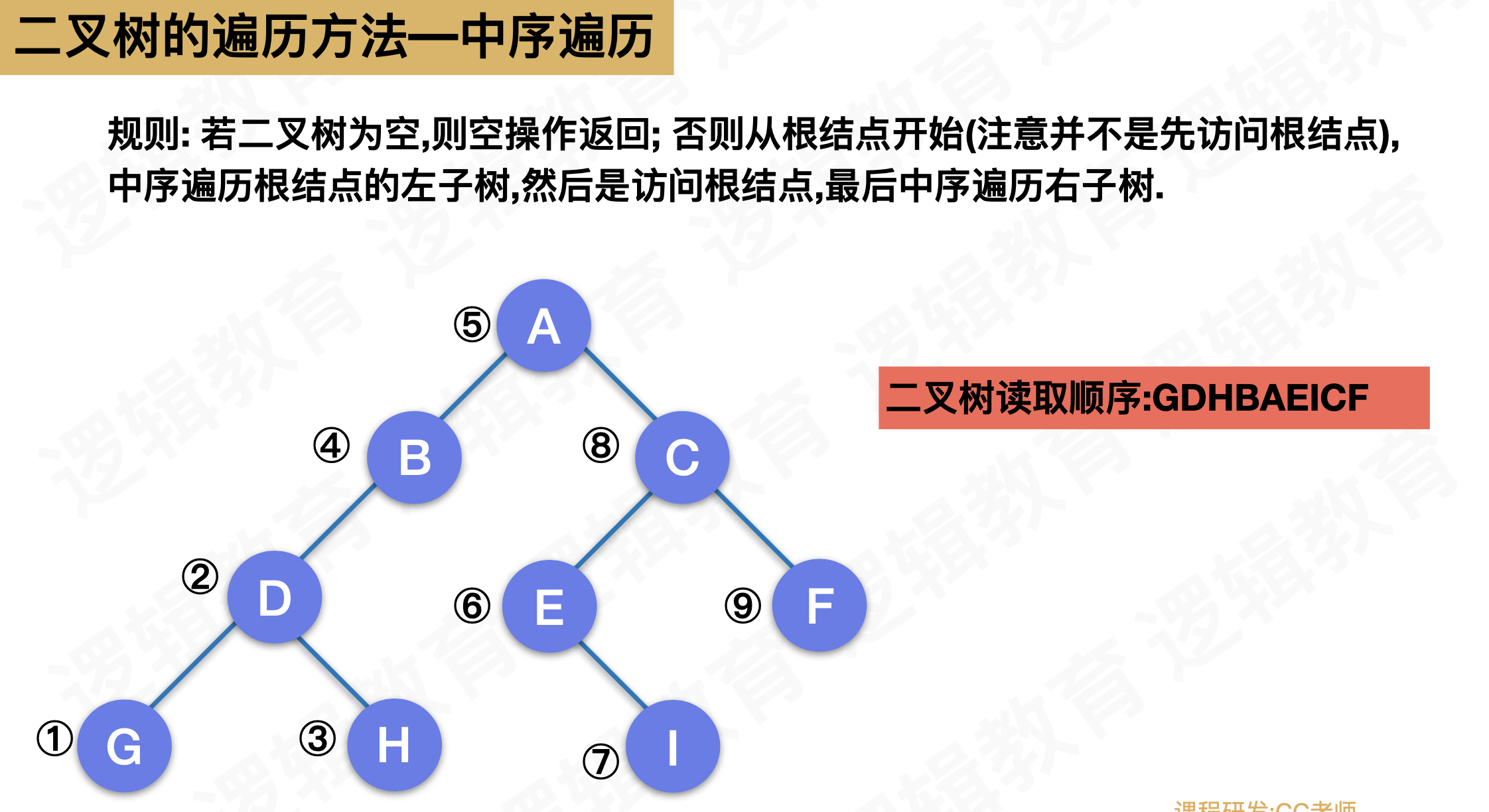
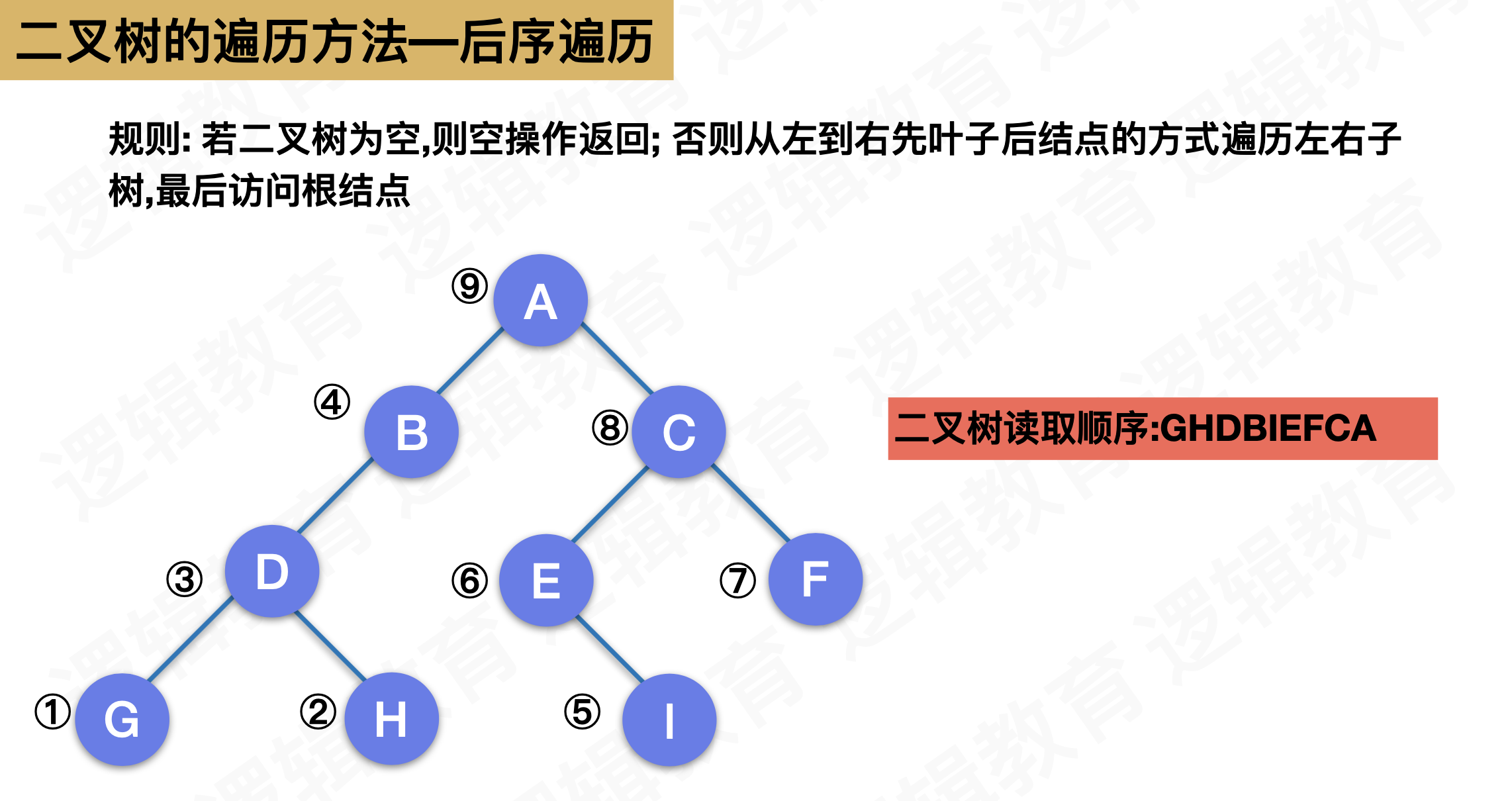
二叉树顺序存储下的前序、后序、中序、层序遍历
- 前序遍历:若二叉树为空,则空操作返回;否则先访问根节点,然后前序遍历左子树,再前序遍历右子树
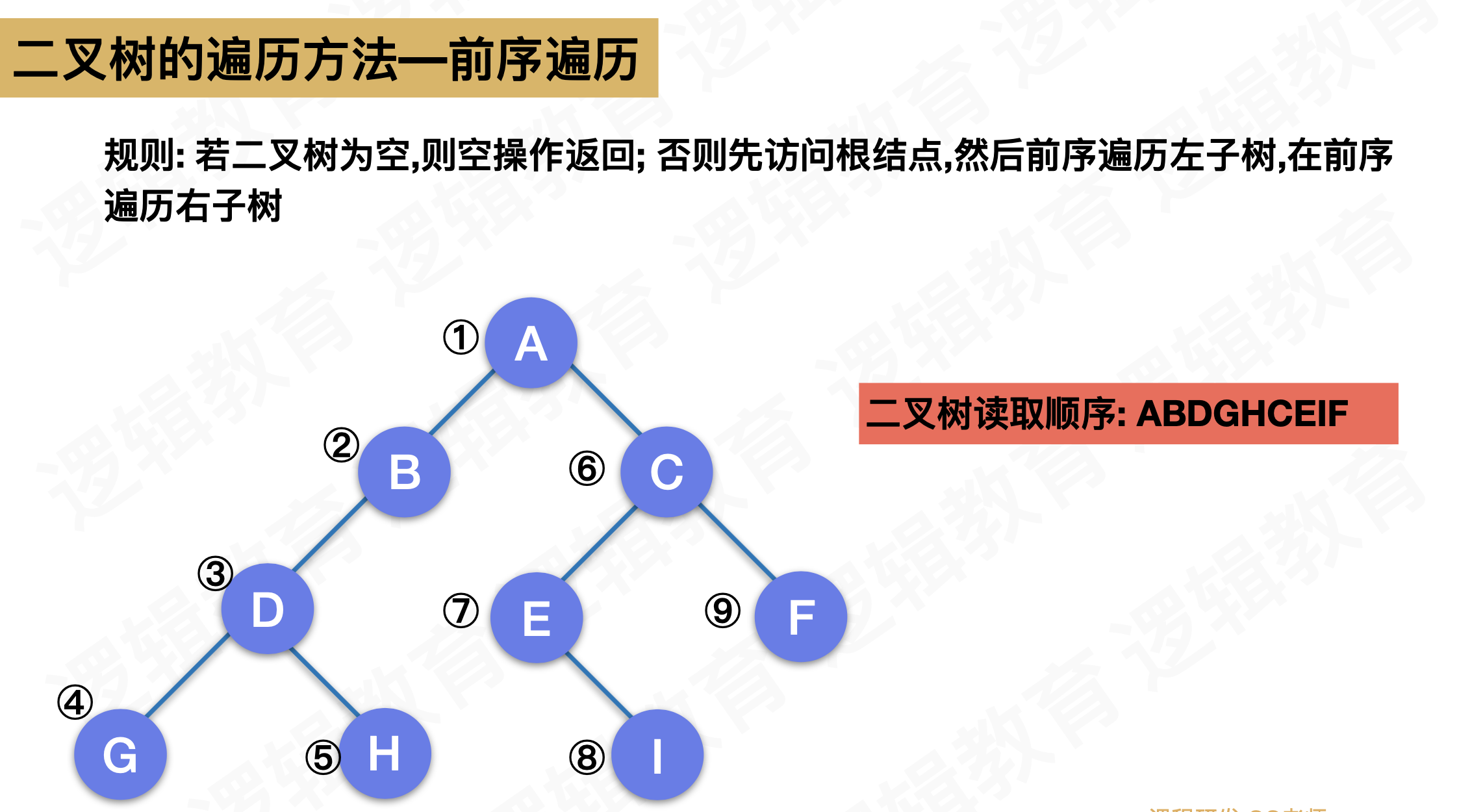
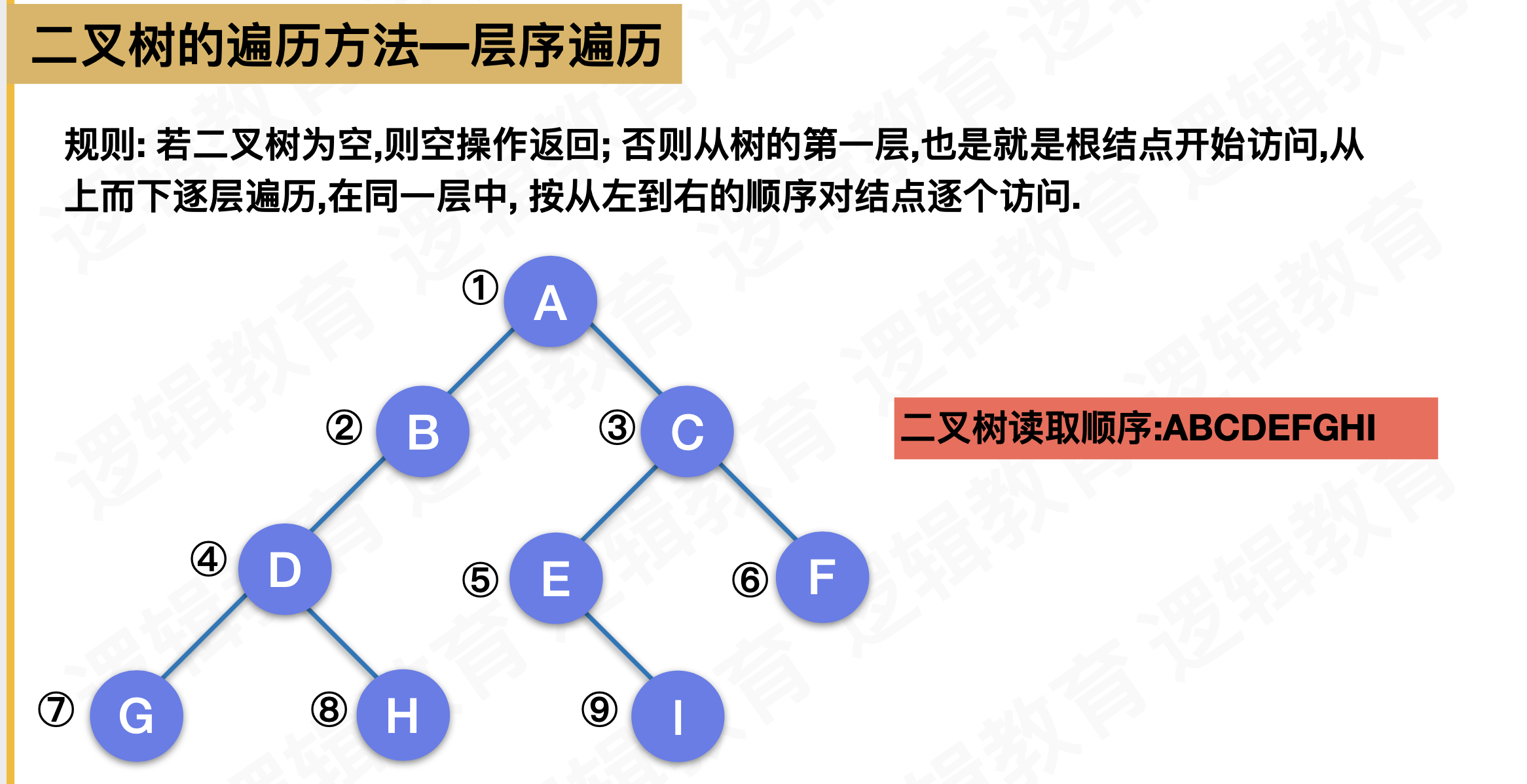
//层序遍历
void LevelOrderTraverse(SqBiTree T){
int i = MAX_TREE_SIZE -1;
while(T[i]==Nil){
i--;
}
for(int j=0; j<=i;j++){
if(T[i]!=Nil)
printf“%d”,T[j]);
}
printf("\n");
}
//前序遍历
void PreTraverse(SqBiTree T,int e){
//打印结点数据
visit(T[e]);
//先序遍历左子树
if (T[2 * e + 1] != Nil) {
PreTraverse(T, 2*e+1);
}
//最后先序遍历右子树
if (T[2 * e + 2] != Nil) {
PreTraverse(T, 2*e+2);
}
}
Status PreOrderTraverse(SqBiTree T){
//树不为空
if (!BiTreeEmpty(T)) {
PreTraverse(T, 0);
}
printf("\n");
return OK;
}
/* 中序遍历
*/
void InTraverse(SqBiTree T, int e){
/* 左子树不空 */
if (T[2*e+1] != Nil)
InTraverse(T, 2*e+1);
visit(T[e]);
/* 右子树不空 */
if (T[2*e+2] != Nil)
InTraverse(T, 2*e+2);
}
Status InOrderTraverse(SqBiTree T){
/* 树不空 */
if (!BiTreeEmpty(T)) {
InTraverse(T, 0);
}
printf("\n");
return OK;
}
/* 后序遍历
*/
void PostTraverse(SqBiTree T,int e)
{ /* 左子树不空 */
if(T[2*e+1]!=Nil)
PostTraverse(T,2*e+1);
/* 右子树不空 */
if(T[2*e+2]!=Nil)
PostTraverse(T,2*e+2);
visit(T[e]);
}
Status PostOrderTraverse(SqBiTree T)
{
if(!BiTreeEmpty(T)) /* 树不空 */
PostTraverse(T,0);
printf("\n");
return OK;
}
二叉树链式存储下相关操作及遍历实现
- 1 打印数据
- 2 构造空⼆叉树T
- 3 销毁二叉树
- 4 创建二叉树
- 5 二叉树T是否为空
- 6 二叉树T的深度
- 7 二叉树T的根
- 8 返回p所指向的结点值
- 9 给p所指结点赋值为value
#pragma mark--二叉树构造
int indexs = 1;
typedef char String[24]; /* 0号单元存放串的长度 */
String str;
Status StrAssign(String T,char *chars)
{
int i;
if(strlen(chars)>MAXSIZE)
return ERROR;
else
{
T[0]=strlen(chars);
for(i=1;i<=T[0];i++)
T[i]=*(chars+i-1);
return OK;
}
}
#pragma mark--二叉树基本操作
typedef char CElemType;
CElemType Nil=' '; /* 字符型以空格符为空 */
typedef struct BiTNode /* 结点结构 */
{
CElemType data; /* 结点数据 */
struct BiTNode *lchild,*rchild; /* 左右孩子指针 */
}BiTNode,*BiTree;
/* 7.2 构造空二叉树T */
Status InitBiTree(BiTree *T)
{
*T=NULL;
return OK;
}
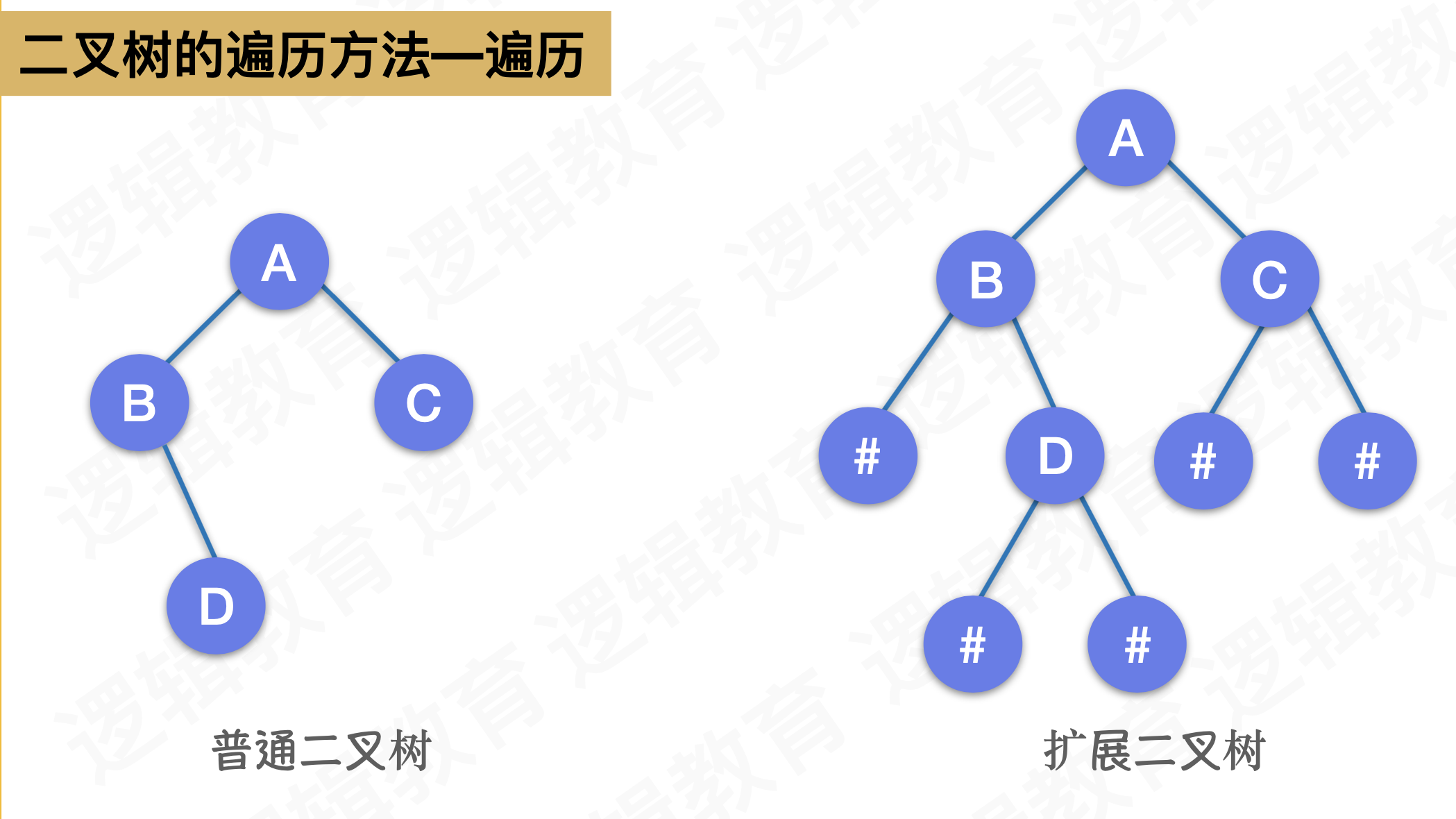
/*7.4 创建二叉树
按前序输入二叉树中的结点值(字符),#表示空树;
*/
void CreateBiTree(BiTree *T){
CElemType ch;
//获取字符
ch = str[indexs++];
//判断当前字符是否为'#'
if (ch == '#') {
*T = NULL;
}else
{
//创建新的结点
*T = (BiTree)malloc(sizeof(BiTNode));
//是否创建成功
if (!*T) {
exit(OVERFLOW);
}
/* 生成根结点 */
(*T)->data = ch;
/* 构造左子树 */
CreateBiTree(&(*T)->lchild);
/* 构造右子树 */
CreateBiTree(&(*T)->rchild);
}
}
/*
7.5 二叉树T是否为空;
初始条件: 二叉树T存在
操作结果: 若T为空二叉树,则返回TRUE,否则FALSE
*/
Status BiTreeEmpty(BiTree T)
{
if(T)
return FALSE;
else
return TRUE;
}
/*
7.6 二叉树T的深度
初始条件: 二叉树T存在
操作结果: 返回T的深度
*/
int BiTreeDepth(BiTree T){
int i,j;
if(!T)
return 0;
//计算左孩子的深度
if(T->lchild)
i=BiTreeDepth(T->lchild);
else
i=0;
//计算右孩子的深度
if(T->rchild)
j=BiTreeDepth(T->rchild);
else
j=0;
//比较i和j
return i>j?i+1:j+1;
}
/*
7.7 二叉树T的根
初始条件: 二叉树T存在
操作结果: 返回T的根
*/
CElemType Root(BiTree T){
if (BiTreeEmpty(T))
return Nil;
return T->data;
}
/*
7.8 前序递归遍历T
初始条件:二叉树T存在;
操作结果: 前序递归遍历T
*/
void PreOrderTraverse(BiTree T)
{
if(T==NULL)
return;
printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
PreOrderTraverse(T->lchild); /* 再先序遍历左子树 */
PreOrderTraverse(T->rchild); /* 最后先序遍历右子树 */
}
/*
7.9 中序递归遍历T
初始条件:二叉树T存在;
操作结果: 中序递归遍历T
*/
void InOrderTraverse(BiTree T)
{
if(T==NULL)
return ;
InOrderTraverse(T->lchild); /* 中序遍历左子树 */
printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
InOrderTraverse(T->rchild); /* 最后中序遍历右子树 */
}
/*
7.10 后序递归遍历T
初始条件:二叉树T存在;
操作结果: 中序递归遍历T
*/
void PostOrderTraverse(BiTree T)
{
if(T==NULL)
return;
PostOrderTraverse(T->lchild); /* 先后序遍历左子树 */
PostOrderTraverse(T->rchild); /* 再后序遍历右子树 */
printf("%c",T->data);/* 显示结点数据,可以更改为其它对结点操作 */
}