动力学网络重构综述本文是对《从数据到结构——动力学网络重构》一文的重新梳理。原文有70多个数学公式，本文会给出关键的公式

原文首发于集智斑图-动力学网络重构综述。文章中涉及到的所有论文，都可以在集智斑图中获取到相关的论文解读资料。

本文是对《从数据到结构——动力学网络重构》一文的重新梳理。原文有70多个数学公式，本文会给出关键的公式和相关引用文献，尽量从实际物理意义的角度来阐述文章的思路。想了解更多详细的公式推导过程，还是建议前往原文阅读。

集智学园还有对本文的视频解读，喜欢看视频学习的可点击上面原文👆的解读资料，或者直接前往观看从数据到结构——动力学网络重构 | 复杂系统自动建模读书会第3期。张博（白楚）老师的解读逻辑清晰，深入浅出。

更喜欢文字版本的可以继续往下👇

背景介绍&& 领域介绍

网络科学是一个跨学科性质非常强的，研究各个领域中各个系统的共性的学科。从最宏大的宇宙星系，到我们生活中随处可见的社交网、信息网，再到生命体的基因、神经系统，都存着各种各样的复杂网络。这些复杂网络都可以是网络科学的研究对象，尤其是希望可以对这些纷繁复杂的网络进行合理的抽象，归纳出一些通用的研究方法。

随着大数据技术和手段的日益发展，我们已经有能力获取到足够丰富的数据，比如我们可以收集到信息网络中每个节点随时间变化的信息，或者我们可以检测到不同时刻蛋白质浓度的变化。那么如何从这些数据中，去挖掘出背后系统更多的网络信息呢？我们现在拥有了巨大的数据财富，此刻需要的，是更加行之有效的数据分析方法。

刚刚所列举的信息网络和基因网络数据，都属于随时而变的动力学网络。复杂系统中的动力学网络是产生数据的重要来源。通过动力学网络，利用收集到的可观测数据，从中揭示隐藏的网络结构和动力学演化规律，是网络数据分析的重要课题。

网络结构和动力学的研究成为物理、数学和各类交叉学科及其重要并受到广泛关注的重要领域。下面是几个研究网络结构的经典模型

Collective dynamics of ‘small-world’ networks

Emergence of scaling in random networks

Exploring complex networks.

而根据网络中的动力学研究网络结构的课题，被称为动力学网络重构。下面列举了一部分近年来这个方向的一些研究进展。

探测复杂系统中的因果关系：这篇文章使用CCM（收敛交叉映射，Convergent Cross Mapping）方法，希望找到变量之间的“CCM因果联系”

Detecting Causality in Complex Ecosystems

群体智慧在鲁棒基因网络推理中的应用：作者比较好地对各种重构方法进行了归类和比较。特别是，作者详细地分析了重构网络中的各种模体（Motif），以及观察不同重构方法更倾向于实现何种模拟。

Wisdom of crowds for robust gene network inference

基于数据的非线性复杂动态系统识别与预测：这篇是用压缩感知的方法进行网络重构

Data based identification and prediction of nonlinear and complex dynamical systems

非线性集体动力学直接网络相互作用的无模型推断：和本文用解析求解的方法不同，这篇是直接运用线性回归的方式来对方程组进行求解，从而解决网络的重构问题。

Model-free inference of direct network interactions from nonlinear collective dynamics

由集体动力学统计揭示物理相互作用网络：这篇是用驱动响应方式进行网络重构

Revealing physical interaction networks from statistics of collective dynamics

更多和动力学重构相关的文献，可以参考张江老师写的复杂网络动力学系统重构文献这条路径，文章梳理了动力学系统重构领域的整体脉络，也包含了丰富的文献。

研究意义

用动力学研究网络结构，无论是实际应用，还是对于网络重构理论，都有非常重要的意义。

现实中存在很多实际系统，人们可以相对容易地获取到系统各个单元的数据，包括社会系统（如金融系统、电力系统、交通系统等）和自然系统（神经网络、基因系统、气象系统等），但是对于系统内部各个单元的相互作用数据，以及系统演化的动力学机制却难以获取。从数据到网络重建，这个需求已经出现在了大量的实际引用中。

另外，动力学重构的研究也有重要的理论意义，因为重构研究其实面临了很多困难：

实际网络非常复杂，网络有大量节点，节点之间有复杂的相互作用。从数据->分析结构信息这个过程会面临各种困难。

这篇是一个数据量小，网络稀疏条件下的重构算法

Reconstructing the topology of sparsely connected dynamical networks

数据中包含很多与网络无关的因素，包括外部干扰，内部未知干扰（噪音）。下面是几篇研究网络中噪声的文献

A synthetic oscillatory network of transcriptional regulators

Scaling of noisy fluctuations in complex networks and applications to network prediction

Noise bridges dynamical correlation and topology in coupled oscillator networks

网络动力学的非线性。面对线性系统，我们可以通过现有数学和统计方法加以处理，但如果动力学是非线性的，就大大增加了问题的难度
数据的缺失。会存在一些数据难以获得（隐藏节点），而这些节点在整个网络中和可测节点同样重要。

下面是研究有关数据缺失问题的部分相关文献 Inferring topologies of complex networks with hidden variables

Detecting hidden nodes in complex networks from time series

Uncovering hidden nodes in complex networks in the presence of noise

本文对上述四种常见的问题，在理论上给出了一套通用的解决方案。

动力学网络重构问题

文章把很多实际系统用以下动力学网络描述（公式1会反复在下文出现，请注意）：

公式1：\frac{dx(t)}{dt} = F(x(t)) + \Gamma(t)

其中 $x(t)$ 是不同时刻节点的状态，可以是向量（一个节点），也可以是矩阵（N个节点）

$F(x(t))$ 是描述自身和相互作用的动力学

F(x(t)) = (F_1(x(t)), F_2(x(t)), · · · , F_N(x(t)))

$\Gamma(t)$ 是各个节点所受到的噪声影响（本文考虑了简单的加性白噪声）

\Gamma(t) = (\Gamma_1(t), \Gamma_2(t), · · · , \Gamma_N (t))

网络重构问题是，在已知部分节点的输出数据的条件下，尽可能求解未知网络内部隐藏的结构信息。即已知 $x(t)^M = (x_{i1} (t), x_{i2} (t), · · · , x_iM (t)), M \ll N$ ，求解 $F_i(x(t)),Q_{ij}$ 其中 $i, j = 1, 2, \dotsm , M$

我们在上文中提到的，网络重构问题中普遍存在的困难，在公式1中都可以体现：

网络规模可能会很大，即 $N\gg1$ ，节点之间的相互作用会非常复杂。
噪声普遍存在，而 $\Gamma_i(t)$ 很可能是未知的，甚至其统计特征 $\hat{Q}$ 也常常是未知的
$F_i(x(t))通常是非线性而且未知的
实际数据通常会有缺失，即 $M\ll N$

本篇论文要讨论的就是如何在上述困难存在的情况下，从数学模型的角度解决动力学网络重构的问题。

虽然公式1包含了很多在网络重构中常见的，且起到重要作用的困难，不过，文章的讨论其实依然基于了很多的假设，另外一些同样重要的困难并未涉及，比如：

噪声的假设过于简单，只是简单的加性白噪声（关联时间很短的噪声）。若外部噪声必须用有色噪声描述（关联时间和动力学时间尺度相比不短），那么上述式子就不再成立

Depicting network structures from variable data produced by unknown colored-noise driven dynamics

没有考虑节点作用不等时的情况，而实际中有时候的节点作用是存在延时的

关于延时的讨论在下面的论文中有所讨论，本文不再涉及。 Reverse engineering of complex dynamical networks in the presence of time-delayed interactions based on noisy time series

Reconstruction of ensembles of coupled time-delay systems from time series

Recovery of couplings and parameters of elements in networks of time-delay systems from time series

线性网络重构

数学原理

首先研究公式1最简单的情况。在这个公式中的 $F$ 是如何体现网络结果的呢？

上面公式的左半边是一个微分方程，右边最简单的线性近似可以看作是一个常数矩阵和状态变量序列的乘积

公式2: \dot{x(t_k)} = \hat{A} x(t) + \Gamma(t'_k),

公式2的性质在统计物理中作为一个基本问题受到广泛关注与讨论，其中与本文的重构问题直接相关的公式是 $\hat{A}\hat{C} + \hat{C}\hat{A^T} =−\hat{Q},$ ，来自下面这篇文献，其中 $\hat{C}$ 为一个噪声与网络结构的关联矩阵

Fokker-planck equation

将这个公式2右乘 $x(t)^T$ ，对一个节点来说，就意味着汇集了当前时刻其他节点的状态特征，最终可以把这个网络方程转化为这样的一个式子：

公式3:\hat{B} = \hat{A}\hat{C} + <\Gamma(t')x(t)^T>

公式其中的 $\hat{B}$ 和 $\hat{C}$ 都可以从观测到的数据中通过一些统计关联计算得到，我们可以理解为， $\hat{B}$ 和 $\hat{C}$ 都是可以从数据中获取的，文章要讨论的还是如何在有噪声的情况下恢复 $\hat{A}$ 。而右侧的第二项，由于假设的是一个简单的噪声，它的尺度远远小于网络内部的涨落，所以信号与当前时刻的噪声统计是不相关的，那么这一项长期的平均观测值应该是0。也就相当于 $\hat{B} = \hat{A}\hat{C}$ ，那么即可求得 $\hat{A}$ ：

接下来，我们加上时间演化的状态，这次回到公式2，跟上一次右乘 $x（t_k)^T$ 不同，这次我们右乘上 $x(t_{k+1})^T$ ，得到了这样的式子。

公式5: \hat{B^+} = \hat{A}\hat{C^+} + <\Gamma(t')x^+(t)^T>

同样的 $\hat{B^+}$ 和 $\hat{C^+}$ 都可以认为是观测得到的，而这里的噪声 $<\Gamma(t')x^+(t)^T>$ ，是当前信号与上一时刻的噪声，两者就不是不相关的了，长期的统计值期望是 $\hat{Q}$ ，也就是说公式5可以写成这样：

还是公式5: \hat{B^+} = \hat{A}\hat{C^+} + \hat{Q}

那 $\hat{A}$ 刚才在公式4中已经得到，这里的 $\hat{Q}$ 我们也就可以通过矩阵计算得出了：

公式6：\hat{Q} = \hat{B^+} - \hat{A}\hat{C^+} - \hat{B} - \hat{A}\hat{C} = \hat{B^+} - \hat{B}

小结

总结一下这个模块。对于一个简单的线性网络来说，相当于只要有一系列的观测数 $X(t)$ ，我们就可以计算出网络结构A，以及影响网络结构的噪声统计 $\hat{Q}$ 。需要注意的是，在有噪声的情况下，各种统计关联矩阵是从可测数据到网络重构的核心，而选择合适的关联矩阵是关键中的关键。

线性网络的实验结果

下面这张图是线性网络的仿真实验结果，考虑了节点数N=100的两组随机线性网络。5%的正相互作用和5%的负相互作用，也考虑了固定连接强度和均匀分布的连接强度。

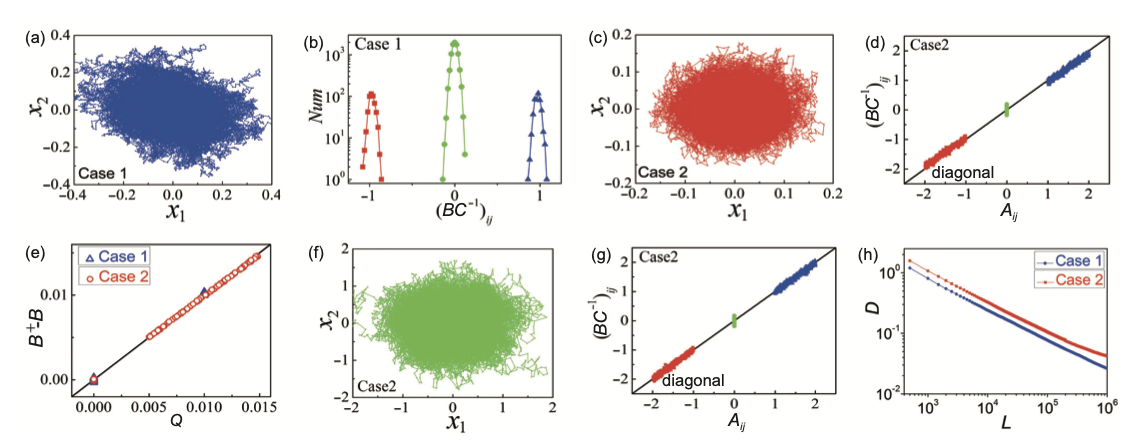
(a)和(c)是两组网络节点在相平面上的投影
(b)和(d)是用公式4（求 $\hat{A}$ ）分别重构(a)和(c)的结果
(e)是公式6（求 $\hat{Q}$ ）推断的噪声与真实情况的对比
(f)和(g)是对网络(c)在噪声提高10倍情况下节点数据在相平面的投影(f)和重构结果(g)
（f）是两个网络的重构精度D

D = \sqrt{\frac{\sum_{i=1}^{N}\sum_{j=1}^{N}{(A_{ij} - A'_{ij})}^2}{N^2}}

实验引用自文献

Solving the inverse problem of noise-driven dynamic networks[J]

非线性网络

线性网络公式2的重构可以选取恰当的关联计算并通过去噪声而建立简单的线性矩阵代数运算式实现, 而非线性网络重构就要复杂得多。

不过有了以上线性网络的基础，非线性网络重构也会相对更好理解。

数学原理

首先我们再回到公式1

在数学物理和非线性科学中我们早就已经熟悉了：任意非线性函数可以用基函数进行线性展开。这里我们可以把 $F_i(x)$ 这个非线性函数作线性展开，即

F_i(x) = \displaystyle\sum_{
\mu=1}^{\infty} \hat{\Re}Y(x(t_k))

其中 $Y(x(t_k))$ 是一组非线性基函数（根据具体领域知识选择合适的基函数）

$\hat{\Re}$ 是一个线性矩阵，当然通常是无穷项的，即

然后同样的，我们对左侧的离散测量做差分近似，最终得到了公式7

公式7：\dot{x(t_k)} = \displaystyle\sum_{
\mu=1}^{\infty} \hat{\Re}Y(x(t_k))+ \Gamma(t'_k)

上述的公式看着开始复杂了起来，但其实只是在说一件事情：我们基于领域知识，或者其他别的方式，选择一个合适的基函数，将非线性动力学网络，转化成一个线性矩阵与一组线性基函数相乘的形式。那么我们接下来，只要求解出这个线性矩阵 $\hat{\Re}$ ，就相当于获得这个网络的结构了。

求解的思路与线性网络类似，在公式7中右乘一个当前时刻的节点状态 $x(t_k)$ ，同样的噪声项为0，最终即可获得这样的一个式子：

其中 $\hat{B}$ 与 $\hat{C}$ 中的所有元素都是可以从数据中显示地计算出来，但是与线性网络不同的是，在这里它们都是无穷维的，所以在运算过程中需要采取截断近似，具体如何截断，文章没有提供统一理论，需要根据实际问题和经验，选择一个足够小，但同时又能满足重构要求的截断

在截断近似之后，公式8就可解了：

至此，非线性网络重构过程完成。

文章使用了多个例子去验证这个非线性网络重构的过程，包括洛伦兹方程(Lorenz)重构问题，高纬非线性网络等，在不同的例子中也给出了如何选取合适的近似截断的详细过程。实验结果均得到了不错的效果。

实验引用自文献

Reconstruction of noise-driven nonlinear networks from node outputs by using high-order correlations

数据缺失情况

在上面线性网络和非线性网络的讨论中，都是假设了网络中所有节点的输出数据都可以获取到。

然而在实际中，很多情况并不会那么理想，往往会存在数据缺失的情况。那么在数据缺失的条件下，我们是否还能重构出网络结构呢？

可能存在未知节点：x(t)^M = (x_{i_1}(t), x_{i_2}(t), \dots, x_{i_M}(t)); M \leq N

这个问题文章也给出了解决方法：空间不够，时间来补

数学原理

在节点时间序列数据中，其实包含了极大的信息量。

x_i(t_1) =x_i(t_1),x_i(t_2),\dots,x_i(t_L); N;i = 1, 2, \dots,N;L\gg 1

我们可以通过这些时间序列，对数据进行扩增操作。

这个思路可以归纳为下述几个关键点：

1. 利用时间标签和差分近似对原始数据做处理。原始数据蕴含的信息除了一阶差分信息之外，还报了节点的高阶变化信息。即对节点的时间序列数据做高阶近似差分。这样可以获得一阶导数、二阶导数，一直到v阶导数。

x_{i_\mu}^{(\gamma)}(t_k) = \frac{x_{i_\mu}^{(\gamma - 1)}(t_{k+1}) - x_{i_\mu}^{(\gamma - 1)}(t_{k-1})}{\Delta t}

这里的 $\gamma$ 是求导阶数，这里假设一直取到 $v$ 阶， $\mu$ 代表当前节点，假设有M个已知节点。

2. 我们认为，原数据和各阶导数数据包含相互独立的信息。那么这样做，就意味着我们会有更多的“已知数据”，原来只有M个节点的数据，现在相当于有vM个。在这种情况下，只要保证 $vM > N$ ，那么方程就可解了。

\begin{cases}
(x_{i_1}(t), x_{i_2}(t), \dots, x_{i_M}(t))\\
(x_{i_1}^{(1)}(t), x_{i_2}^{(1)}(t), \dots, x_{i_M}^{(1)}(t))\\
\vdots\\
(x_{i_1}^{(\gamma)}(t), x_{i_2}^{(\gamma)}(t), \dots, x_{i_M}^{(\gamma)}(t))\\
\vdots\\
(x_{i_1}^{(v)}(t), x_{i_2}^{(v)}(t), \dots, x_{i_M}^{(v)}(t))

\end{cases}

这种方法可用来有效弥补缺失信息对网络重构的影响。 $v$ 的选择于前文的截断类似，同样需要根据具体问题和实际的经验寻找到一个最合适的值。

当然，这也是有代价的，如果直接使用上述式子去求解，其实会发现最终的重构结果并不好，因为在我们做高阶微分的时候，数据的噪声也被放大了，作者在这里引入了一个简单方法，其中 $D(t)$ 是 $\Omega$ 窗口内的测量数据，通过这样陪平滑技术最终让重构达到了理想的效果

\bar{D}(t_k) = \frac{1}{\Omega}\sum_{l=1}^{\Omega}D(t_{k+l-1})

数据缺失的实验结果

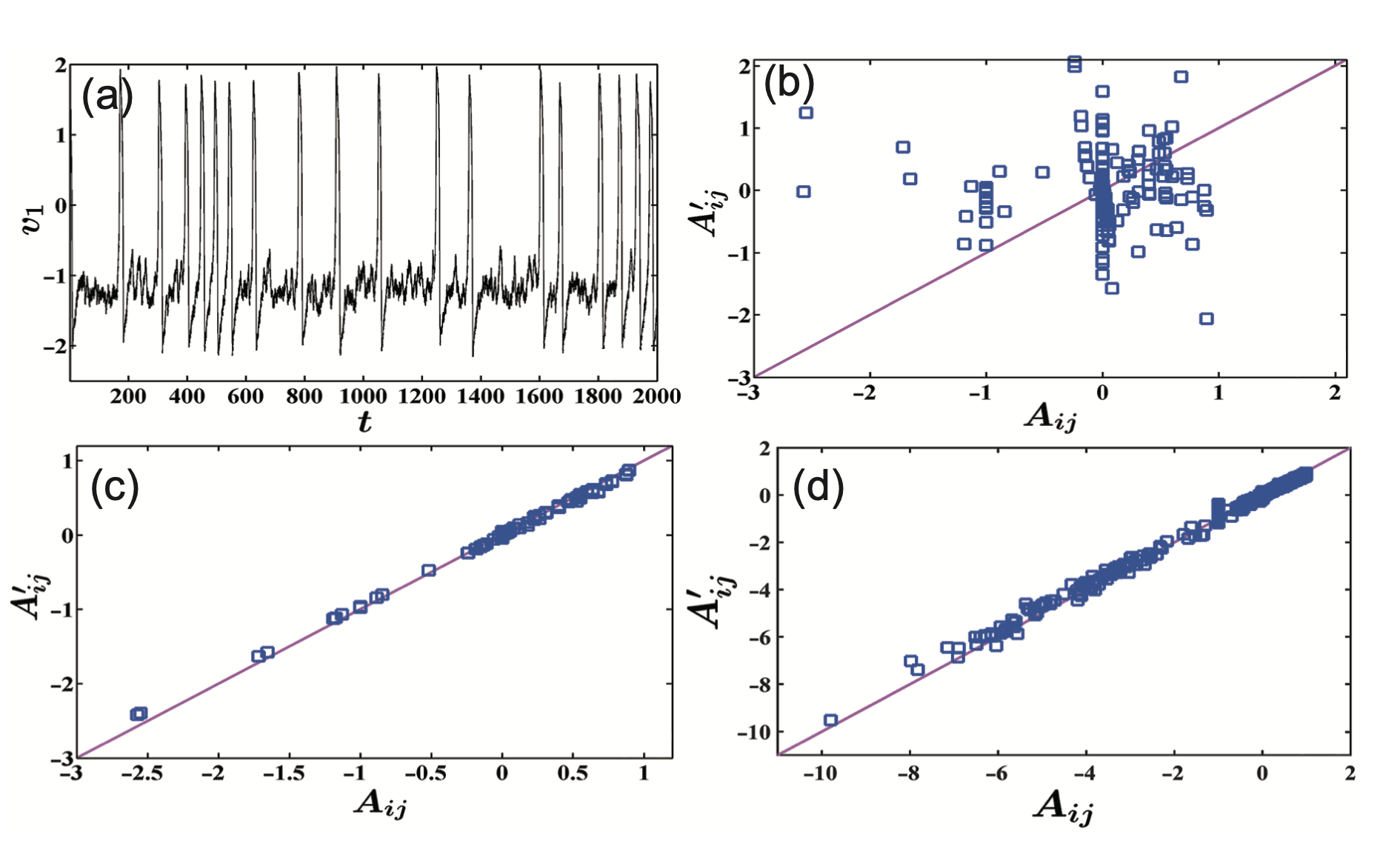
(a)是网络中单个节点的时间序列
(b)和(c)是未做平滑和做了平滑后的重构效果
(d)是扩大节点数量后的重构效果

实验引用自文献： Reconstruction of noise-driven nonlinear dynamic networks with some hidden nodes[J]

利用噪声“局部重构”

另外文章还提出了一个很有意思的思路：在数据缺失的情况下，我们可以利用噪声，去获取到局部的结构信息

在数据缺失较多，或者噪声太大的情况下，全局的网络其实就很难恢复了，几乎是不可恢复的了。不过在有些场合，比如相比于全局的网络，我们更希望知道局部的网络结构；或者有时候，我们仅能获取到很少的数据，但依然想从数据中获取一定成都的结构信息。

局部的重构其实也是一件比较困难的事情，尤其是在网络系统是封闭的时候。

然而，当我们把网络跟外界产生交互，让其变成一个半开放的系统，这件事情就变成可能了。就好比一个黑箱中，如果只能观察到其中的1～2个点，不论是黑箱中全局的还是局部的结构，我们都无法获取到。但是，当我们跟黑箱产生交互的时候，通过观察黑箱对外部交互的反应，那么能获取的信息就更多了。

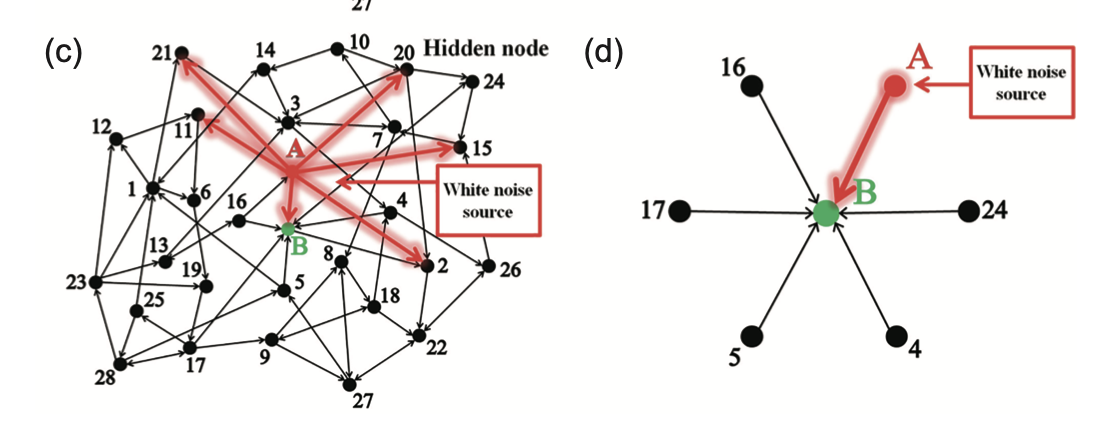
(c) 图表示，如果对A节点施加一定的外界驱动，A对其他节点的作用就可能在众多未知的作用中突显出来
(d) 如果A节点受到的驱动作用使得A对B的作用大大增强，从而在众多隐藏作用中显示出来，在该情形下仅获取A和B这两个节点的数据就可能推断A对B的作用。

通过快速变化的噪声，我们能够提供这样的驱动，使在数据极端缺失的条件下，使得重构两个节点之间的相互作用成为可能。

原文中有一大串的公式，证明这个思路的可行性。在此就不详细列出。

全文总结

本文综述了通过分析动力学网络产生的数据重构网络连接结构和系统演化规律的问题，在如何处理网络结构复杂性，噪声影响，动力学非线性及测量数据缺失等常见困难方面提出了具体的处理方法。

要强调的主要有以下三点

统计关联计算的重要性，选取恰当的关联量是关乎重构成功与否的关键。
充分挖掘和利用数据内包含的信息
噪声的作用和利用。噪声不一定是一个需要被消除的负面因素，有时候具有特定性质的噪声能够对网络重构起到积极的作用

网络重构问题在自然科学和社会科学的广阔领域具有重大意义，同时由于其面临的诸多困难在理论研究中又极具吸引力，它是当前大数据分析的一个重要领域。本文只是讨论了如何处理网络重构中几个常见的困难，而向更深层次的拓展和将这些方法应用于实际数据分析和真实系统重构将是我们面临的重大挑战。