Delay line 延迟线

今天我们将讨论 Delay 和 Vibrato 两种音频特效的技术原理和实现细节。

Delay 和 Vibrato 都是基于 Delay line 实现的。Delay line 作为音频特效中重要的基础组件，它很容易实现，并且稍作修改就能够应用实现于不同的音效。

Delay line 非常简单，它能功能是将一个信号进行延迟。通过使用多条 delay line，并加以不同的信号延迟，然后将这些信号相加在一起，我们就能够创建大量的音频特效。

在模拟信号中，delay line 的实现相当复杂，需要引入物理扩展（例如弹簧）来延迟波的传播。

在数字信号中，delay line 通常使用 ”循环缓冲区” 的数据结构来实现延迟。循环缓冲区本质上可以用一个数组实现，用一个索引来指向下一个存放信号的位置，当索引超过缓冲区大小时，将其重新置于开始位置。这样一来，就像往一个圈里顺时针填数据，当我们需要延迟信号时，计算逆时针回退的个数即可。

下面是 delay line 的一种实现，更多细节大家可以参看代码

template <typename T>
class DelayLine
{
public:
    void clear() noexcept
    {
        std::fill(raw_data_.begin(), raw_data_.end(), T(0));
    }
    /**
     * return the size of delay line
     */
    size_t size() const noexcept
    {
        return raw_data_.size();
    }

    /**
     * resize the delay line
     *
     * @note resize will clears the data in delay line
     */
    void resize(size_t size) noexcept
    {
        raw_data_.resize(size);
        least_recent_index_ = 0;

        clear();
    }

    /**
     * push a value to delay line
     */
    void push(T value) noexcept
    {
        raw_data_[least_recent_index_] = value;
        least_recent_index_ = (least_recent_index_ == 0) ? (size() - 1):(least_recent_index_ - 1);
    }

    /**
     * returns the last value
     */
    T back() const noexcept
    {
        return raw_data_[(least_recent_index_ + 1) % size()];
    }

    /**
     * returns value with delay
     */
    T get(size_t delay_in_samples) const noexcept
    {
        return raw_data_[(least_recent_index_ + 1 + delay_in_samples) % size()];
    }
    
     /**
     * Returns interpolation value
     */
    T getInterpolation(float delay) const noexcept
    {
        int previous_sample = static_cast<int>(std::floorf(delay));
        int next_sample = static_cast<int>(std::ceilf(delay));
        float fraction = static_cast<float>(next_sample) - delay;

        return fraction*get(previous_sample) + (1.0f-fraction)*get(next_sample);
    }

    /**
     * set value in specific delay
     */
    void set(size_t delay_in_samples, T new_val) noexcept
    {
        raw_data_[(least_recent_index_ + 1 + delay_in_samples) % size()] = new_val;
    }

private:
    size_t least_recent_index_{0};
    std::vector<T> raw_data_;
};

Delay 延迟

Delay 音效非常简单，但应用非常广泛。最简单的情况下，将声音进行延迟并与原始信号相加就可以使的乐器的声音更加生动活泼，或者用更长时间的延迟，来达到二重奏的效果。很多熟悉的音效（例如 Chorus、Flanger、Vibrato 和 Reverb）也是基于 Delay 实现的。

Basic Delay 基本延迟

Basic delay 会在指定延迟时间后播放音频。根据应用的不同，延迟时间可能从几毫秒到几秒，甚至更长。这里是一小段 basic delay 算法结果。Basic delay 通常也被称为 Echo(回声）效果。

Basic delay 算法原理部分很简单，通常是将带有延迟的信号与原始信号相加。其中 表示输出信号，表示原始信号，表示延迟（单位是采样个数），表示延迟信号的增益

利用 Z 变换，得到传递函数为：

因为传递函数 的所有极点都在单位圆内，因此 basic delay 在所有情况下都是稳定的。

Dalay with Feedback 反馈延迟

Basic delay 使用场景比较受限，因为它仅仅产生单个回声。大多数音频延迟单元还具有反馈控制，它能够将延迟输出的信号再发送到输入，如下图。反馈使声音不断重复，如果反馈增益小于 1，那么每次回声都会变得更加安静。从理论上讲，回声将永远重复，但它们最终会变得非常安静，以至于你无法听到。

根据上图，我们可以写出反馈延迟的差分方程：

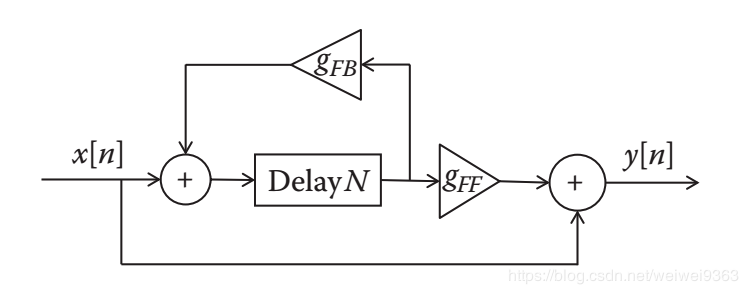
然后可以转换为只与 和 相关差分方程：

计算其传递方程：

因此，系统的极点在 ，这就说明当 时系统是稳定的。这个结果符合直觉，因为只有反馈增益小于1时，回声才会随着时间越来越小。

这里是反馈延迟的算法输出。可以听到反馈延迟效果很像我们在大山里喊叫的效果，比起 basic delay，反馈延迟有多次回声，每次回声音量逐渐变小。

反馈延迟的实现大致如下，通过 delay line 来获取延迟信号，并且往 delay line 中记录带有反馈的信号。如果 feedback 为0，那么反馈延迟将退化为 basic delay。

void DelayEffect::processBlock(AudioBuffer<float> &buffer)
{
    const int num_channels = buffer.getNumChannels();
    const int num_samples = buffer.getNumSamples();

    for(int c = 0; c < num_channels; ++c)
    {
        float* channel_data = buffer.getWritePointer(c);
        auto& dline = dlines_[c];
        size_t delay_samples = delay_length_in_sample_[c];

        for(int i = 0; i < num_samples; ++i)
        {
            const float in = channel_data[i];
            const float delay_val = dline.get(delay_samples);
            float out = 0.0f;

            out = (dry_mix_ * in + wet_mix_ * delay_val);

            dline.push( in + feedback_ * delay_val);

            channel_data[i] = out;
        }
    }
}

Vibrato 颤音

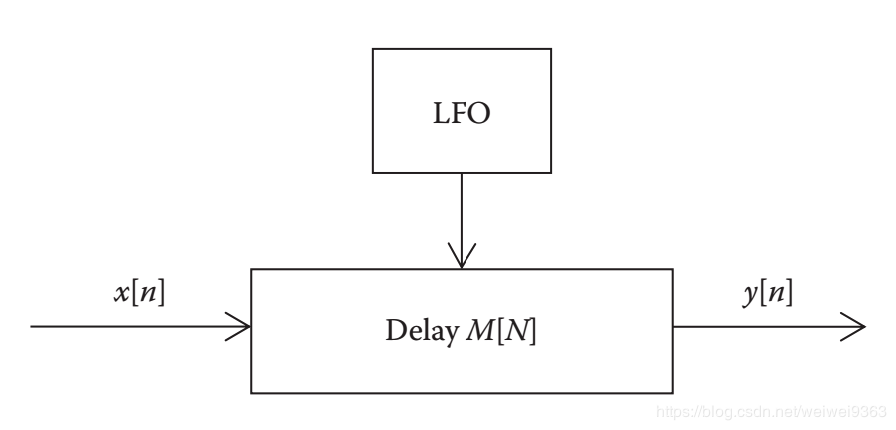
颤音指的是音调周期性微小变化。传统意义上，颤音并不是音效效果，而是歌手和乐器演奏者使用的一种技术。例如在小提琴上，通过在指板上有节奏地前后摇动手指，稍微改变琴弦的长度来产生颤音。但是在音频信号中，我们可以使用调制的 delay line 来实现颤音。

前面提到的两种延迟算法，它们的延迟长度是固定，不随时间变化的那种。颤音与它们最大的不同在于其延迟长度随着时间变化而变化，而这种变化会导致音调的变化，这里我们举个例子来说明，假设：

这时候 ：

也就是说，原来信号频率提升了 倍。如果 那就是降低了频率 频率的变化和 无关，只和 有关

Low-Frequency Oscillator 低频振荡器

为了达到颤音的效果，我们需要模拟那种音调周期性变化的感觉，而延迟长度的变化会引起音调变化，因此如果我们让延迟长度发生周期性变化，那么音调也是周期性变化的。

为了延迟的长度周期性变化，我们可以用一个低频振荡器(Low-Frequency Oscillator; LFO)来控制它，以正弦 LFO 为例，公式为：

其中，调节变换的范围；是 LFO 的频率，影响音调的变化周期；表示采样率。音调的变化可以计算为：

因此音调的变化是个周期函数，一会上一会下的。

这里是颤音算法的输出结果，颤音应用到人声上会产生一种滑稽的效果，挺有趣的。

颤音的实现大致如下，通过 lfo 来得到延迟的长度，根据长度从 delay line 中获取数据。有一点与之前不同的是，当延迟长度不是整数时，我们采用了插值的方法，这样可以让信号更加平滑。

void VibratoEffect::processBlock(AudioBuffer<float> &buffer) {
    const int num_channels = buffer.getNumChannels();
    const int num_samples = buffer.getNumSamples();
    float phase = 0.0f;

    assert(num_channels <= dlines_.size());

    for(int c = 0; c < num_channels; ++c)
    {
        phase = phase_;
        float* channel_data = buffer.getWritePointer(c);
        auto& dline = dlines_[c];

        for(int i = 0; i < num_samples; ++i)
        {
            const float in = channel_data[i];

            // get delay from lfo
            float delay_second = sweep_width*lfo_.lfo(phase, LFO::WaveformType::kWaveformSine);
            float delay_sample = delay_second * getSampleRate();

            // get interpolation delay value
            channel_data[i] = dline.getInterpolation(delay_sample);

            // push input to delay line
            dline.push(in);

            // update phase
            phase += lfo_freq*invert_sample_rate_;
            if(phase >= 1.0f)
            {
                phase -= 1.0f;
            }
        }
    }

    phase_ = phase;
}

总结

以上介绍了延迟和颤音两种音效，并给出了详细实现，它们都是基于 delay line 实现的，简单却又有用。

音频特效专栏

• 音频特效：Delay 和 Vibrato
• 音频特效：Flanger 和 Chorus