需求

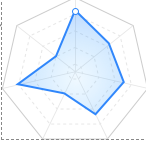
最近有个需求，需要做个蛛网图，然后还可以动态变化，每5秒需要重新定位圆点需要一次移动到每条线上，类似下面图1

解决办法1

这个需求其实不难，难点就是在如何定位到折线图的各个坐标，首先想到的是根据svg的左上点定位，依次计算坐标。 比如计算目前图中的圆点的坐标就是 x坐标是图的宽度w/2, y坐标是图的高度2/h*(1-rate) rate是所占该分支的比率

可以看到这样计算，由于所选的坐标参考，所以每个分支的计算都非常困难，特别麻烦。

解决办法2

这里可以改变我们的参考坐标，由于上一次的解决办法就是坐标参考选的有问题，导致每个坐标的计算都非常麻烦。所以问题就是如何找到新的参考坐标。 可以通过增加一个g元素，通过以下代码，把参考坐标移动到中间，也就是七边形的中心

<g tranlate=(w/2, h/2)></g>

然后就可以计算坐标了。 但是这里计算还是有个问题，以为我们的第一次坐标是如下图的圆点所在位置

也就是说开始的时候，我们实在图中1的位置上，所以当我们计算坐标的时候，必须从1那个地方开始。

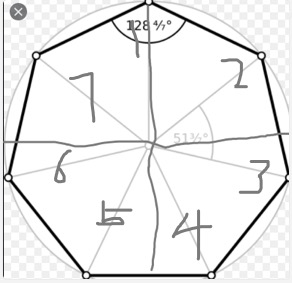
这里假设圆的半径为r, 圆形的坐标为（0， 0）
如果按照正常的从3坐标开始计算的话，依次就是

(0 +r * Math.cos(Math.PI * 5 /14), 0+r * Math.sin(Math.PI * 5 /14))
(0 +r * Math.cos(Math.PI * 9 /14), 0+r * Math.sin(Math.PI * 9 /14))
(0 +r * Math.cos(Math.PI * 13 /14), 0+r * Math.sin(Math.PI * 13 /14))
(0 +r * Math.cos(Math.PI * 17 /14), 0+r * Math.sin(Math.PI * 17 /14))
(0 +r * Math.cos(Math.PI * 21 /14), 0+r * Math.sin(Math.PI * 21 /14))
(0 +r * Math.cos(Math.PI * 25 /14), 0+r * Math.sin(Math.PI * 25 /14))

但是需要从1的位置开始计算，所以我们开始一次赋予坐标分别为

(0 +r * Math.cos(Math.PI * 21 /14), 0+r * Math.sin(Math.PI * 21 /14))
(0 +r * Math.cos(Math.PI * 25 /14), 0+r * Math.sin(Math.PI * 25 /14))
(0 +r * Math.cos(Math.PI * 1 /14), 0+r * Math.sin(Math.PI * 1 /14 ))
(0 +r * Math.cos(Math.PI * 5 /14), 0+r * Math.sin(Math.PI * 5 /14))
(0 +r * Math.cos(Math.PI * 9 /14), 0+r * Math.sin(Math.PI * 9 /14))
(0 +r * Math.cos(Math.PI * 13 /14), 0+r * Math.sin(Math.PI * 13 /14))
(0 +r * Math.cos(Math.PI * 21 /14), 0+r * Math.sin(Math.PI * 21 /14))

这样就可以利用一个简单的函数计算出各个分支的坐标了。

如果任何一段代码，让你觉得不舒服，写的不爽，就是时候想想是不是需要找个别的方法，重新写下。