二十一 Discrete-Time Second Order System
1拉普拉斯变换的性质
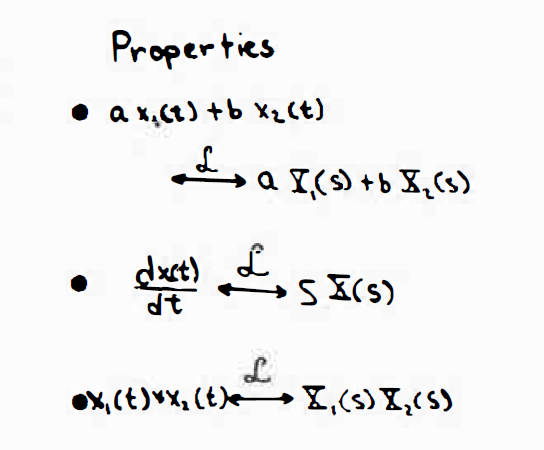
收敛性分析:
★if a LTI system is stable,h(t)绝对可积,傅里叶变换H(ω)收敛,拉普拉斯变换系统函数H(Ω)的ROC包含jω(虚轴)[见二十收敛性分析结论④]
★if a LTI system is casual,则h(t)=0 when t<0,h(t)是一个右侧时间函数,拉普拉斯变换系统函数H(Ω)的ROC在最右极点的右边
综上:

example:一阶微分方程 求出了系统函数的拉普拉斯变换,如果要求其拉普拉斯逆变换,由于不确定收敛域,必须通过已有信息来确定!
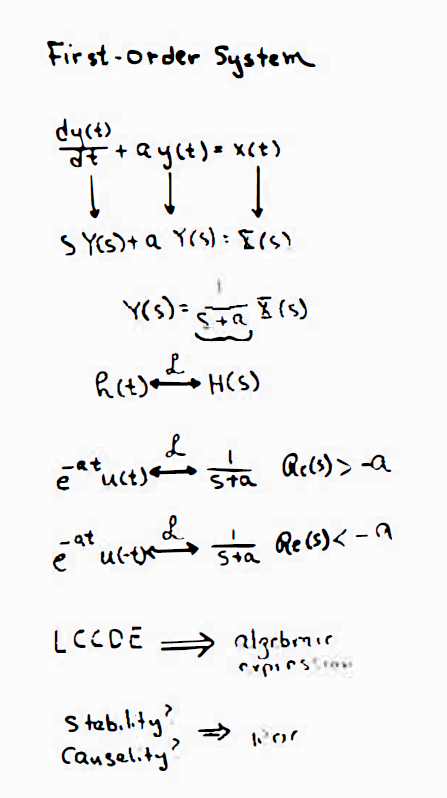
stable:ROC包含jω
casual:ROC在最右极点的右边
2二阶系统
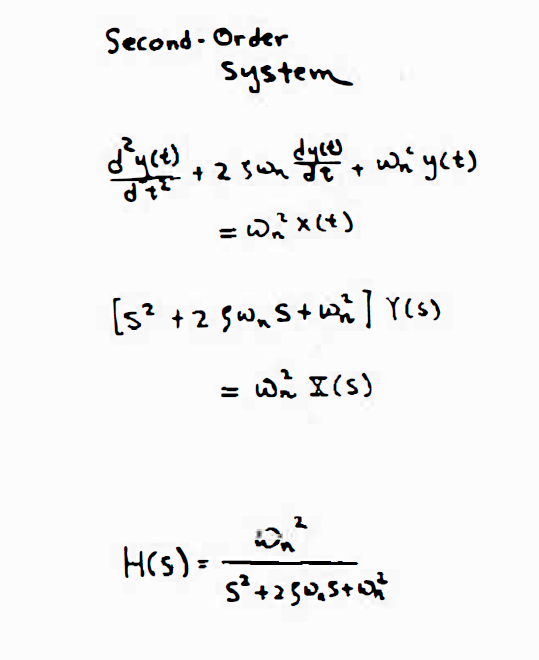
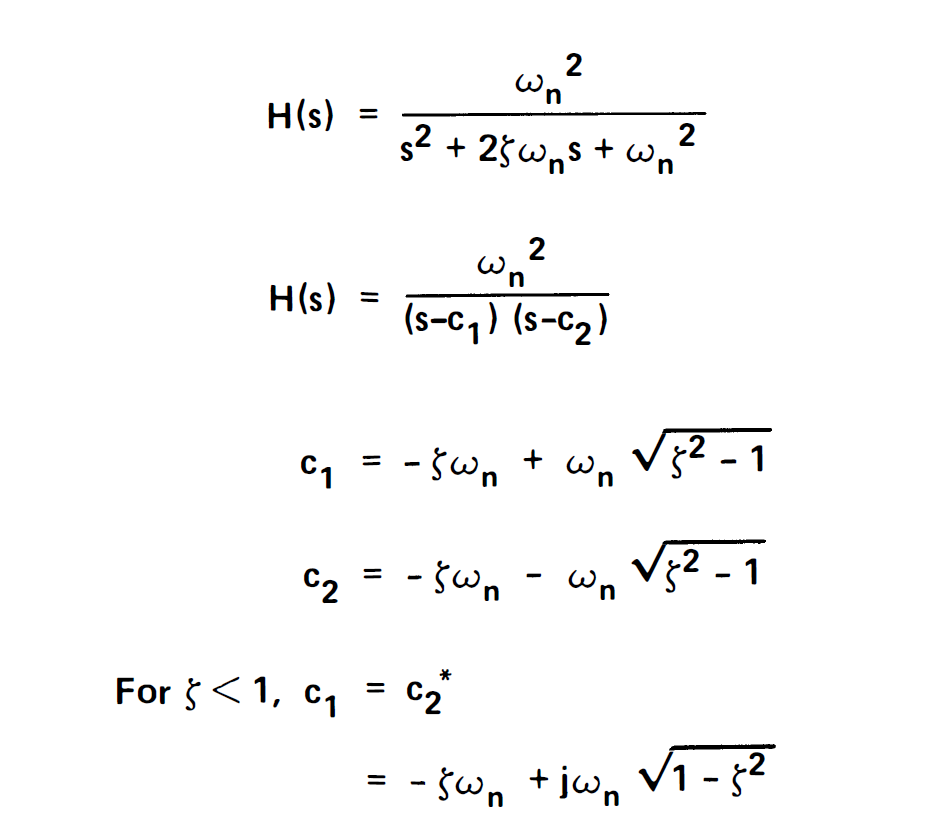
2.1二阶系统的频率响应
|H(jω)|:ωn方除以两个极点与向上移动的jω顶点连线长度
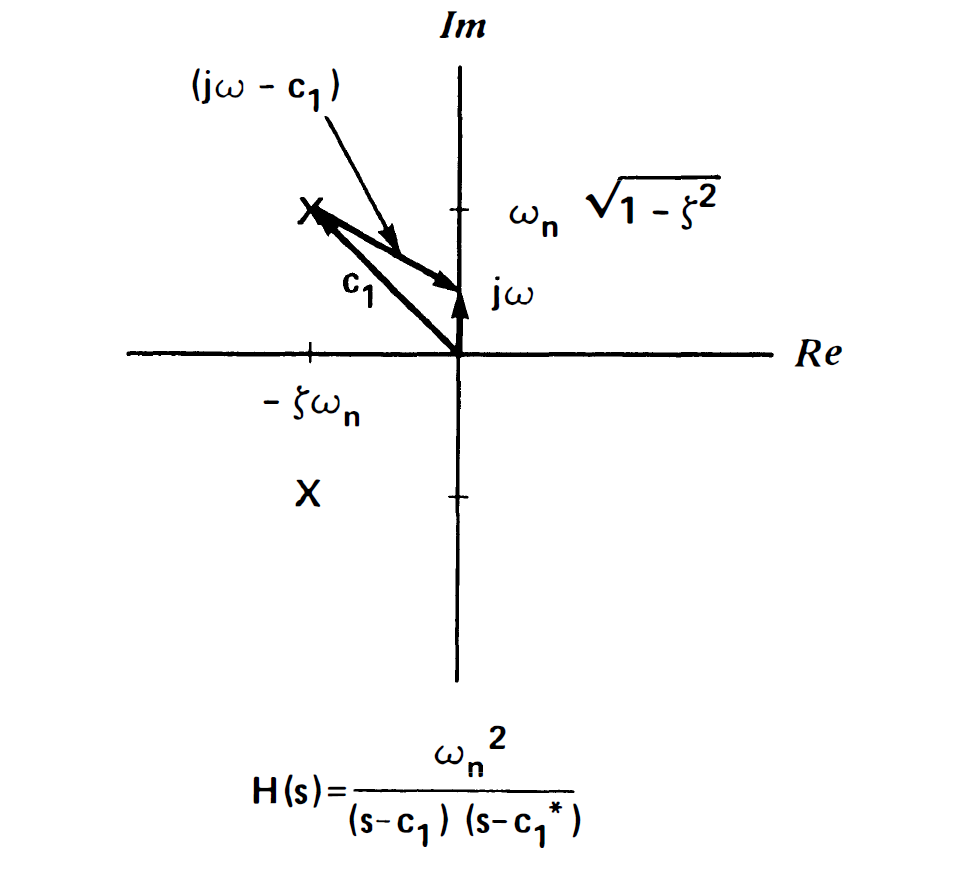

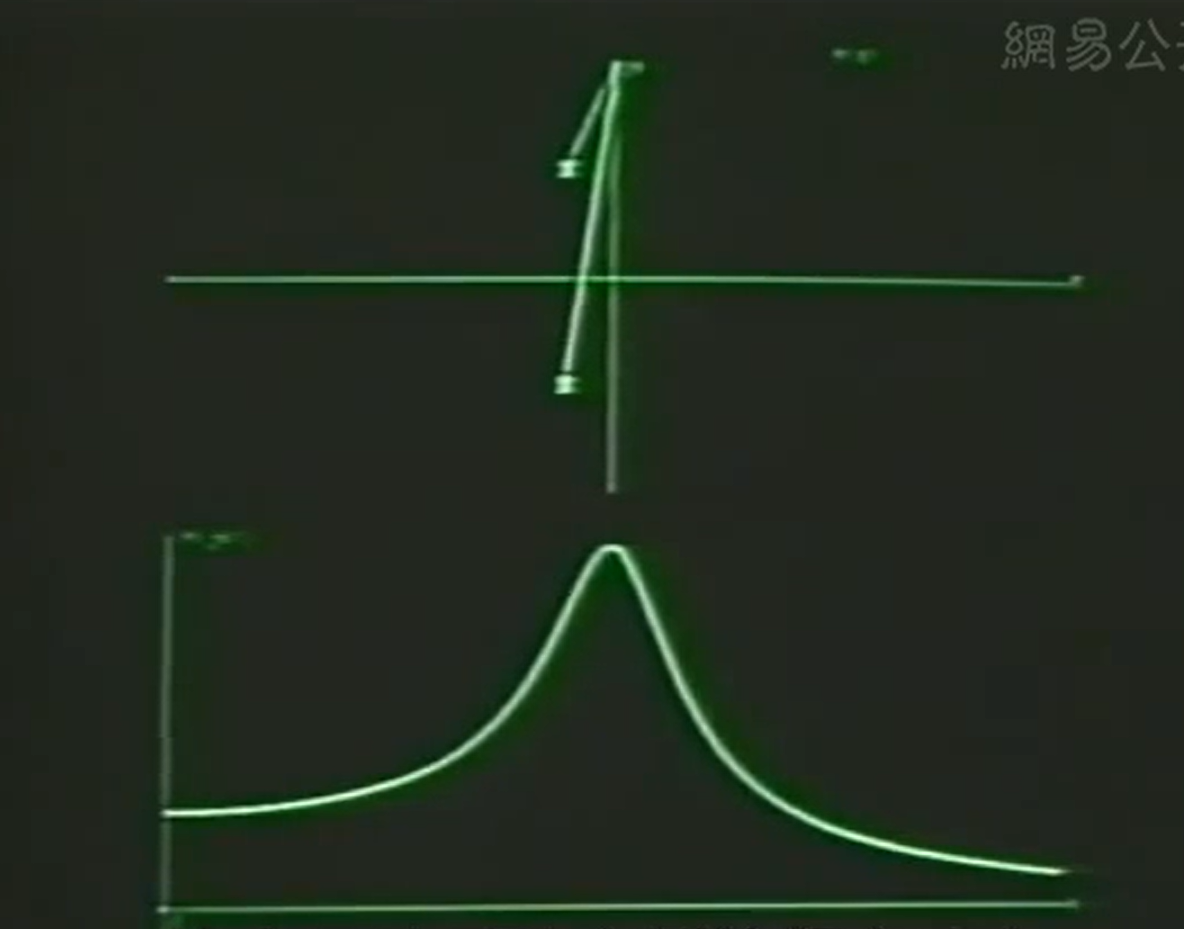
改变极点位置:
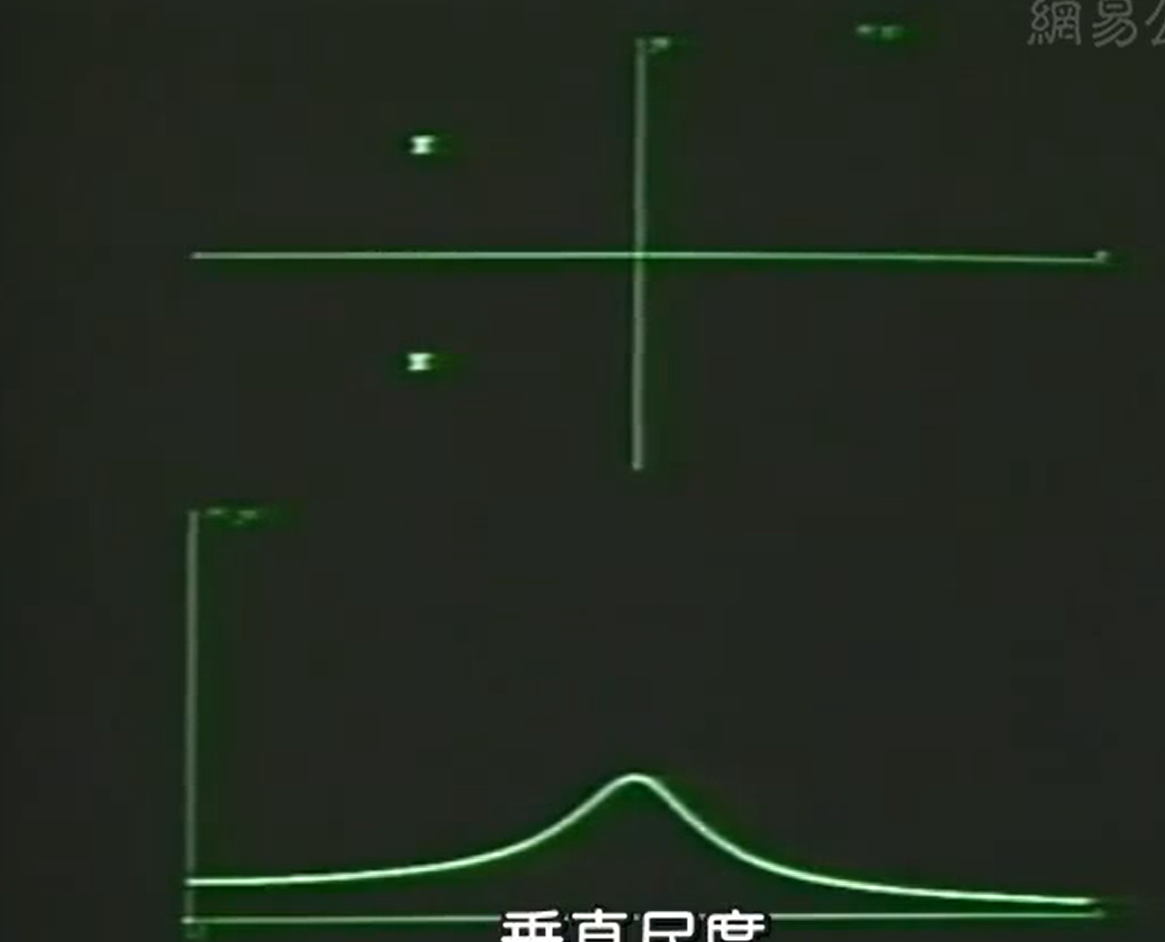

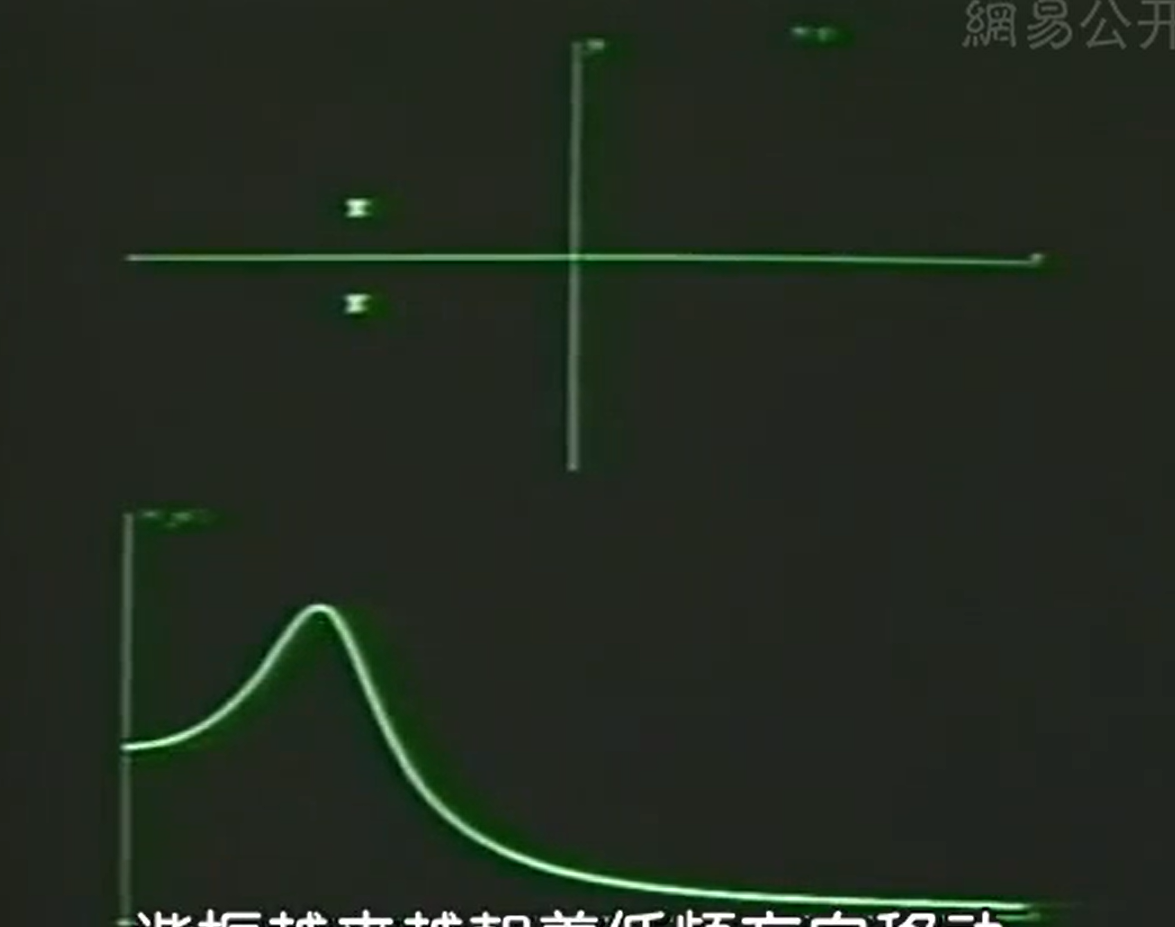
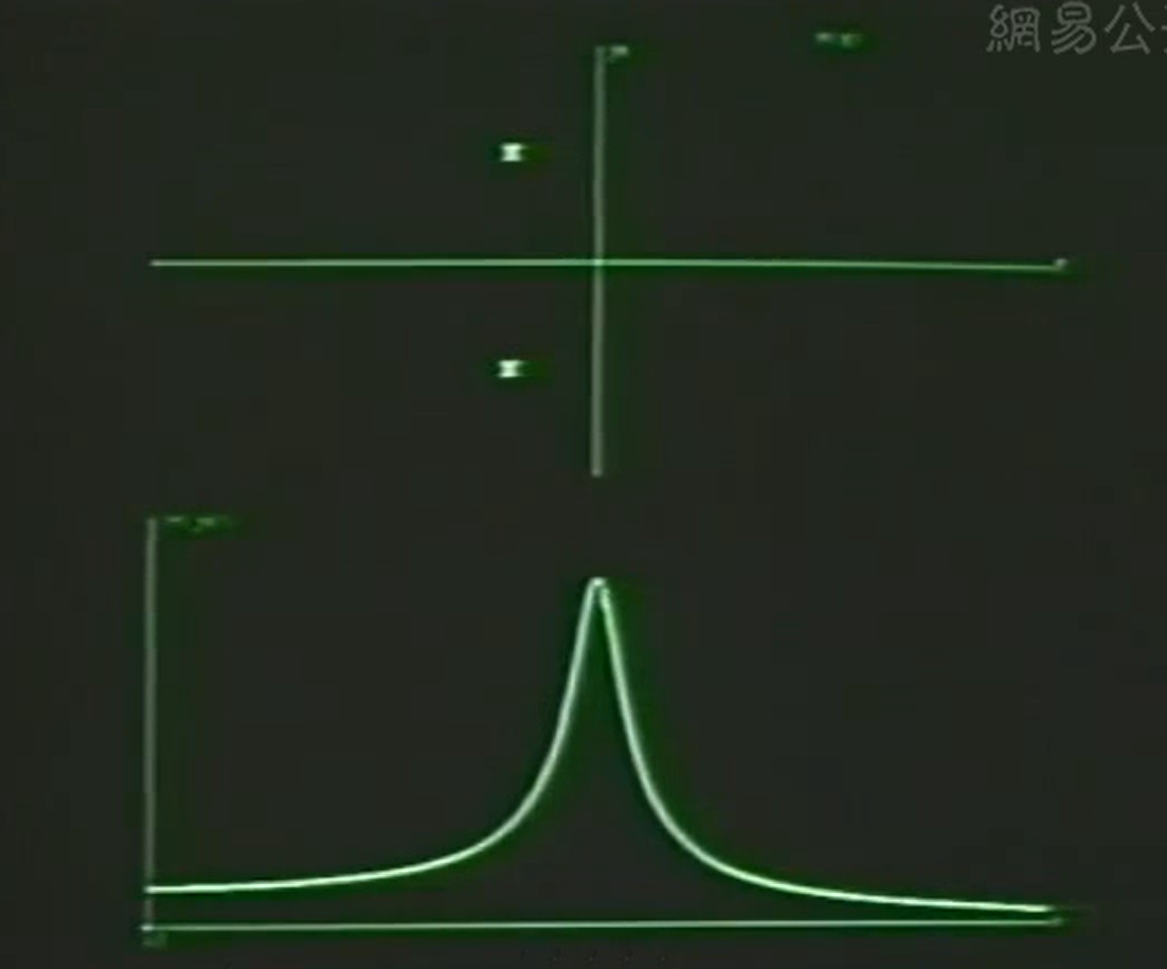
远离虚轴

结论: The frequency of the resonance(谐振频率)(H(Ω))与极点距离实轴位置有关,谐振的宽窄和极点距离jω距离有关
ζ变小,极点靠近jω轴,频率响应会变得尖锐
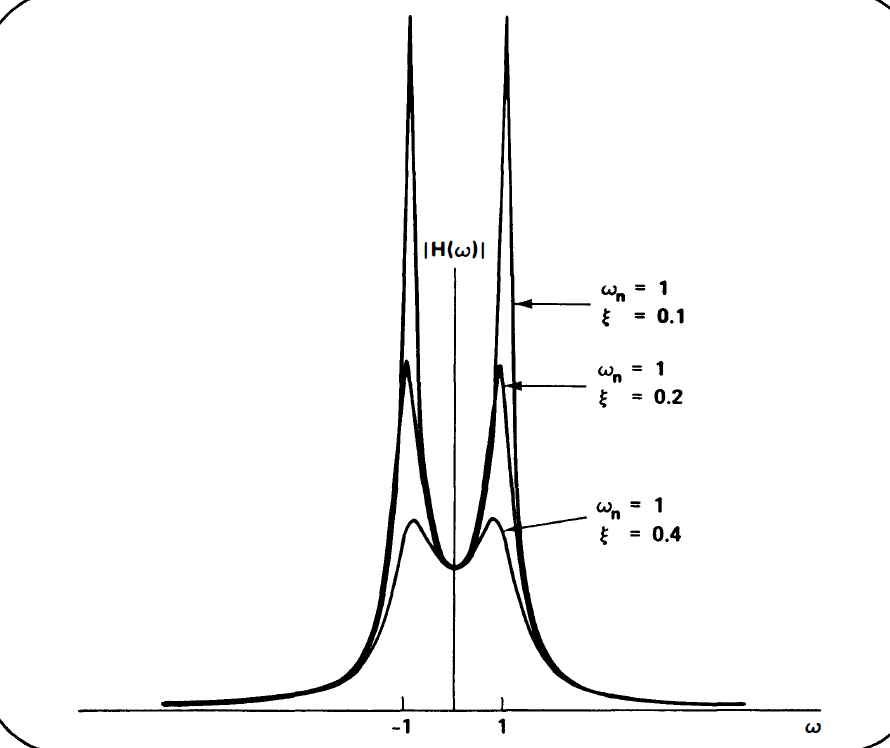
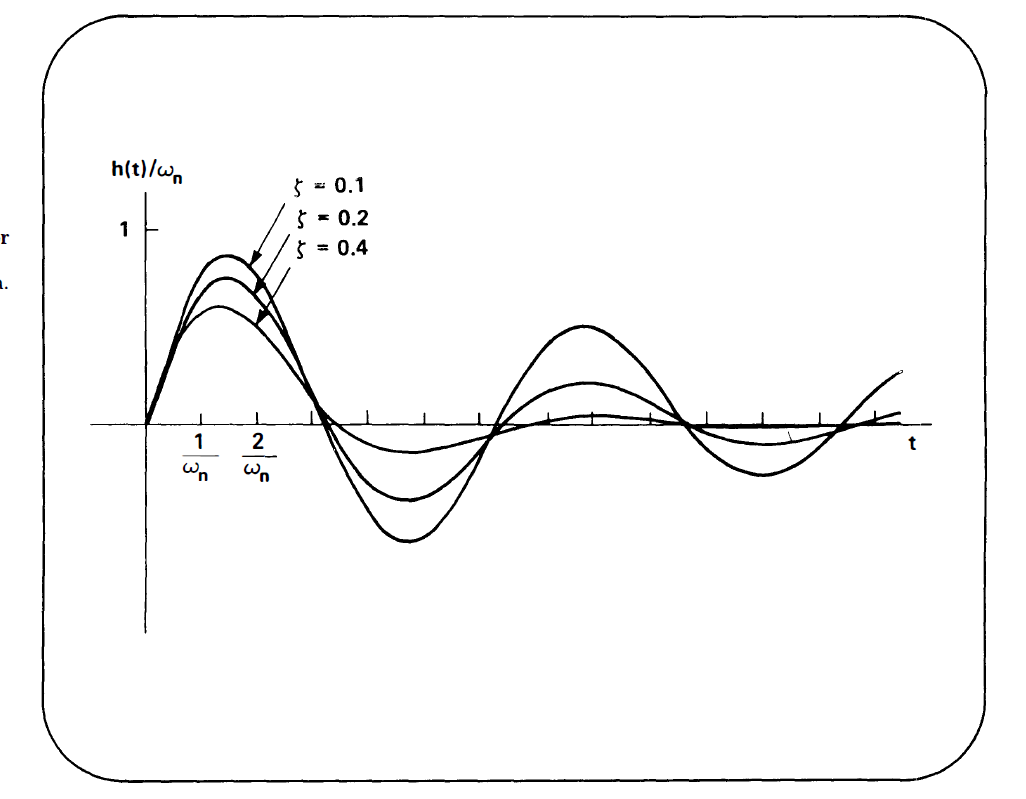
2.2 二阶系统的时域响应
ζ变小,阻力变小,越振荡,越难以收敛
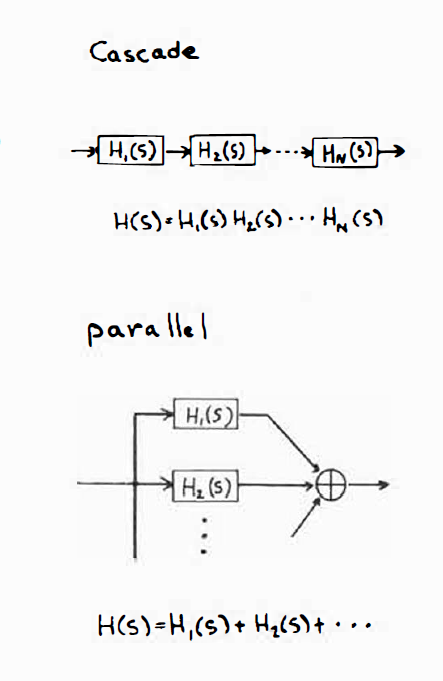
2.3 系统的串并联
n个二阶系统串联或并联后得到的是系统