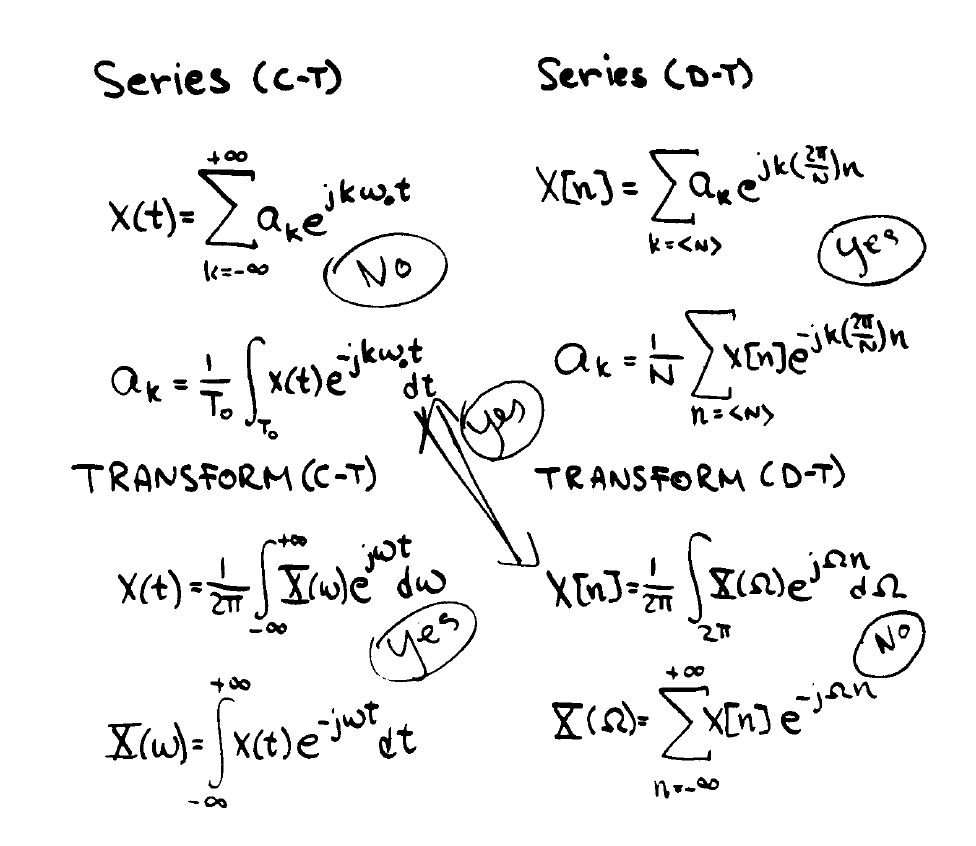
十一 Discrete-Time Fourier Transform

1 对称性

example:
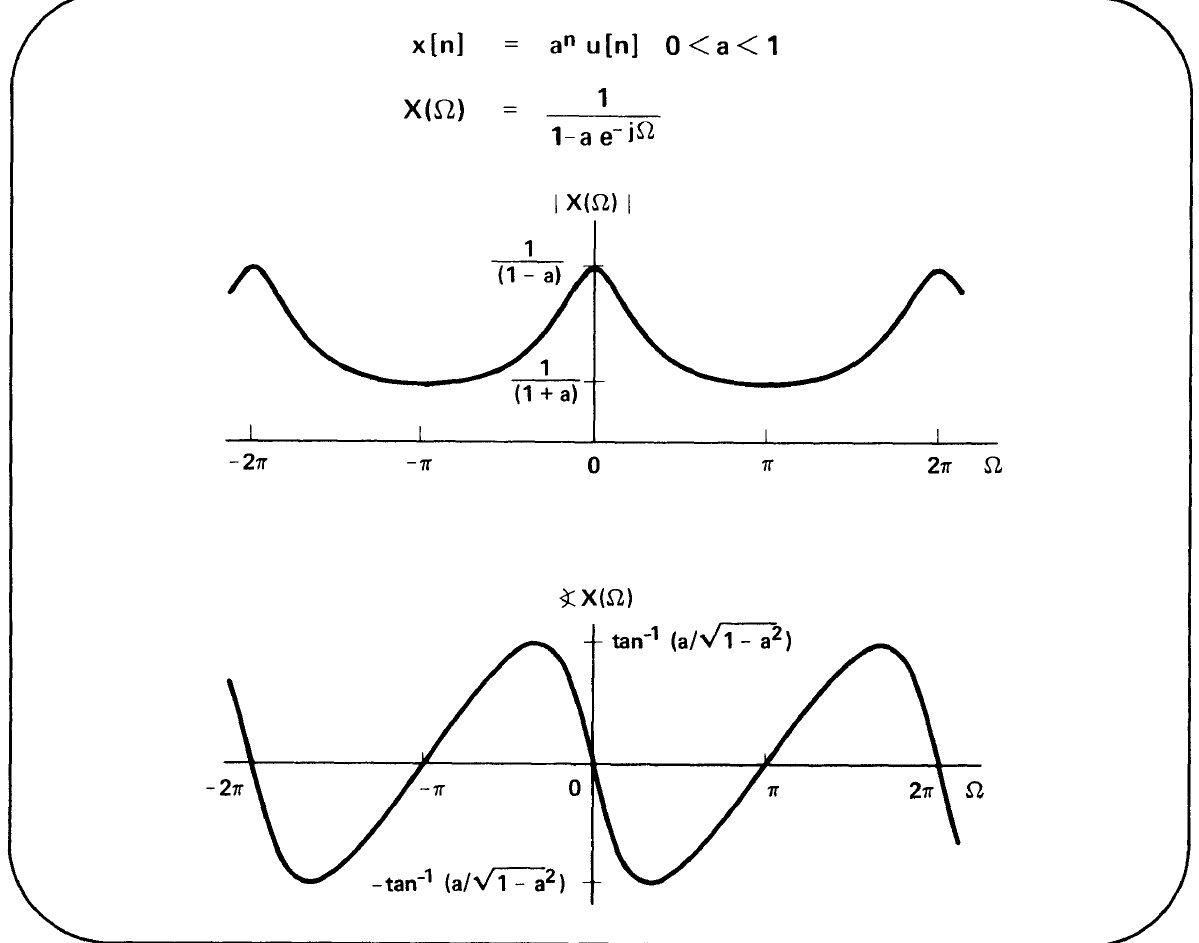
2 其他性质
time shift corresponded to a linear phase,时移对应一个线性相位

★3 卷积特性
直观解释见九
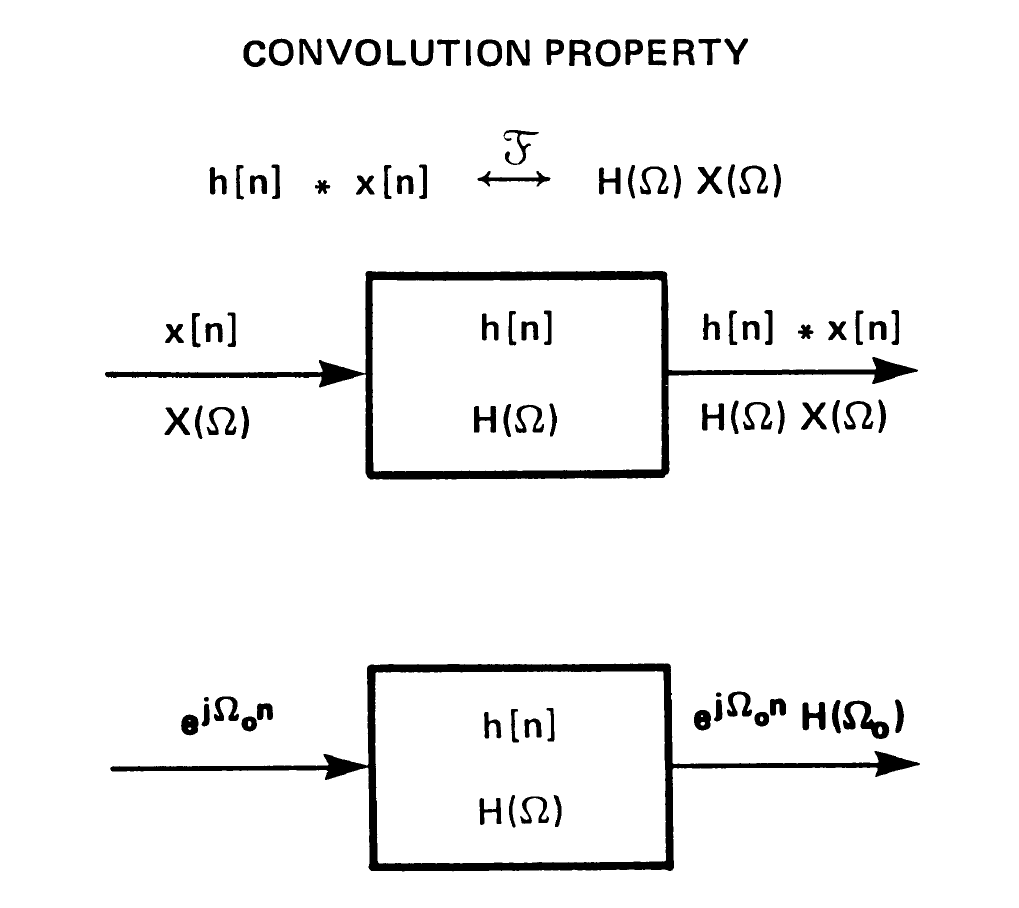
3.1 应用:滤波器
与连续case不同,由于复指数具有周期信,离散低通滤波的波形也应该是无限多个具有周期性的,而不像连续低通滤波仅一个方波。
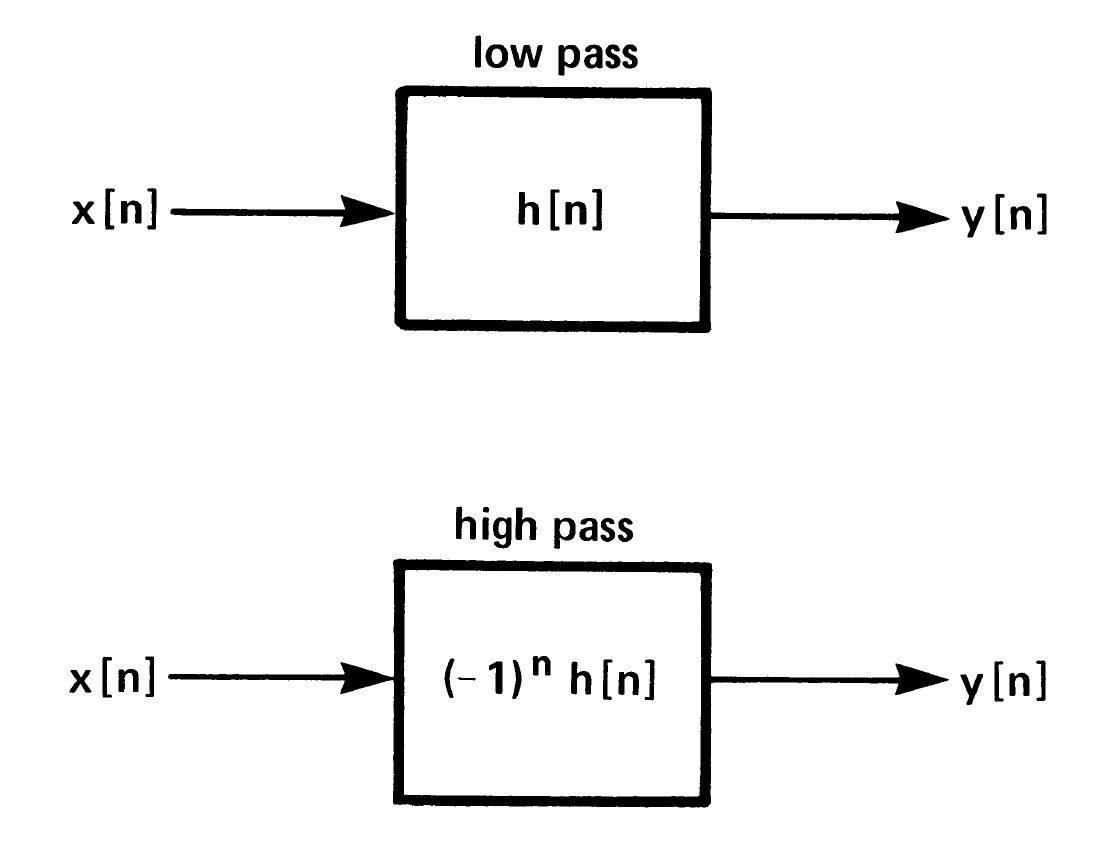
离散低通滤波器:
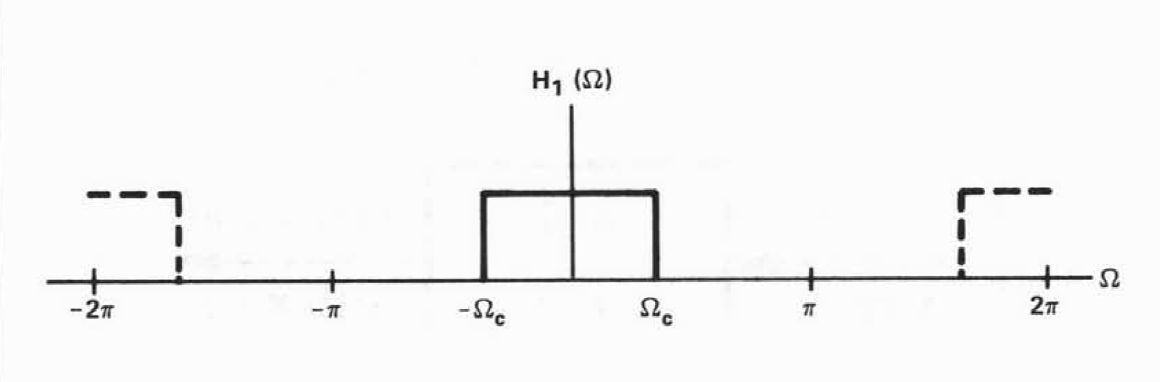
离散高通滤波器:
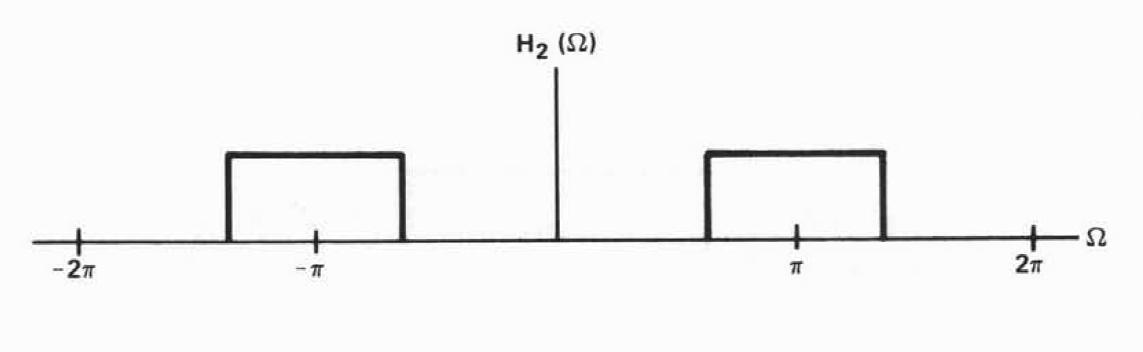
连续高通滤波的高频率是无穷大,离散高通滤波的最高频率是Π
3.2 应用:一阶差分方程的求解
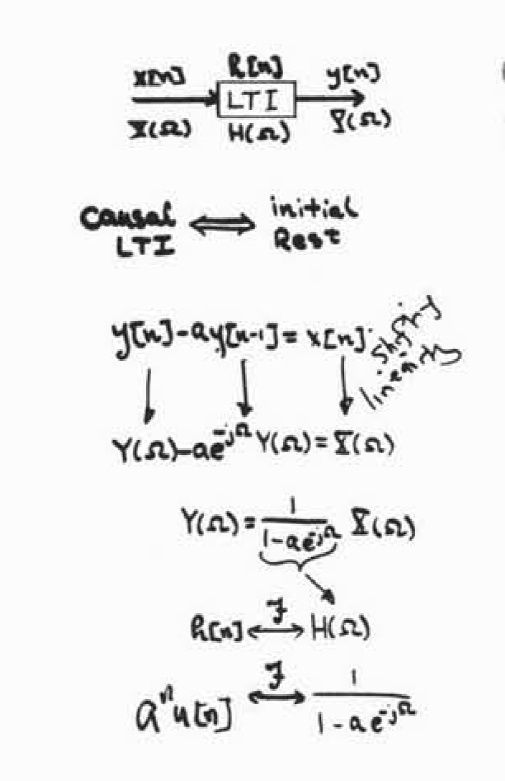
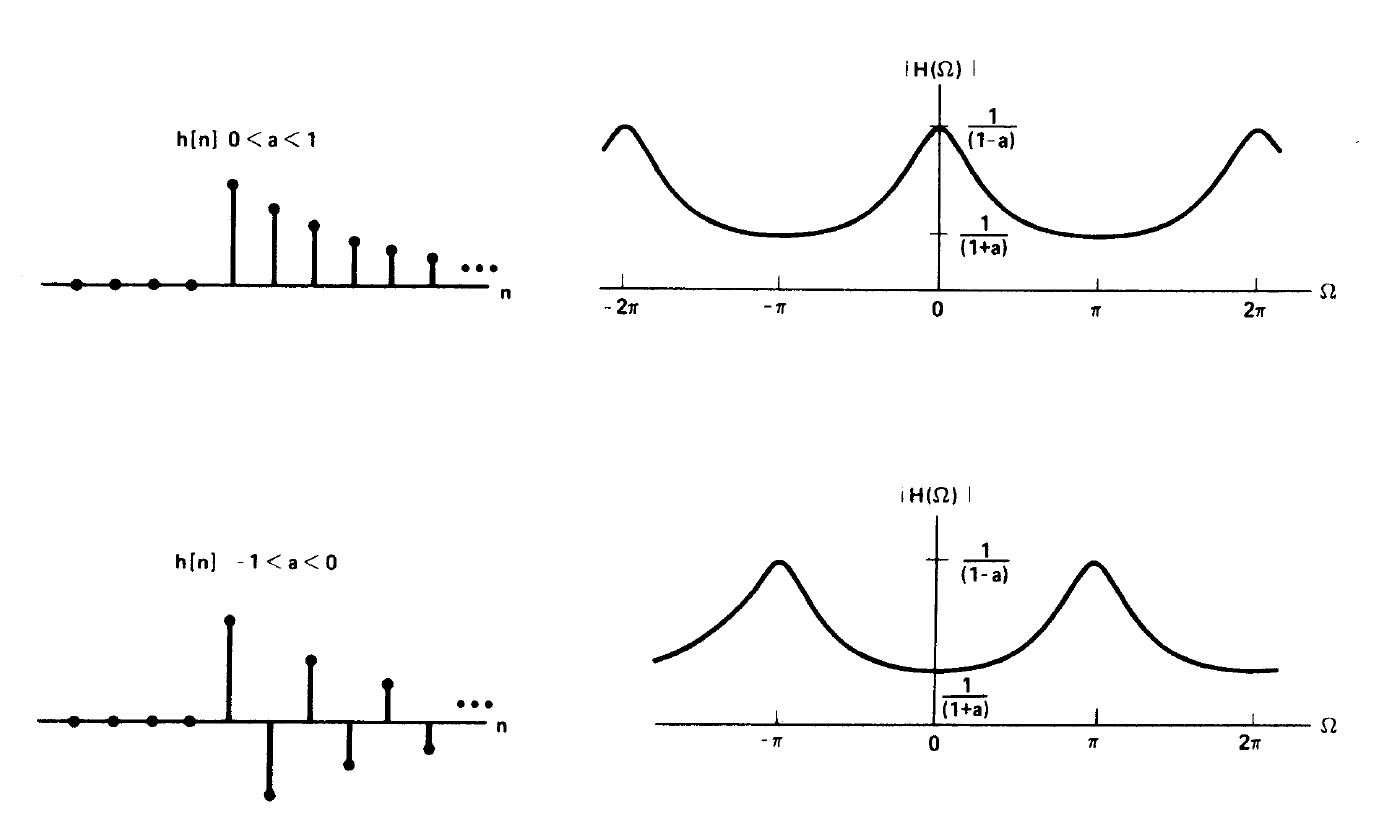
对于的系统来说,当0<a<1,
就是低通滤波器,当-1<a<0,
就是高通滤波器:
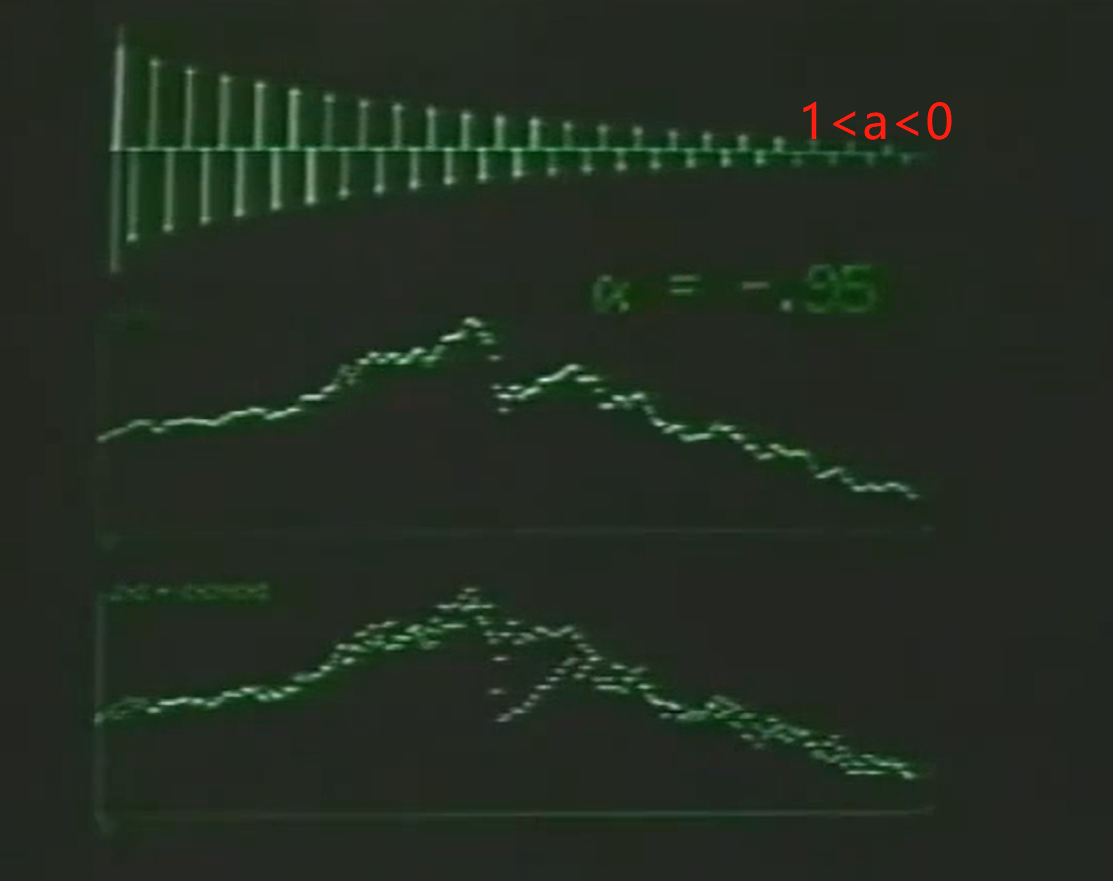
example:道琼斯指数滤波器案例(使用一阶差分方程作为滤波器):
低通滤波使得曲线更平滑
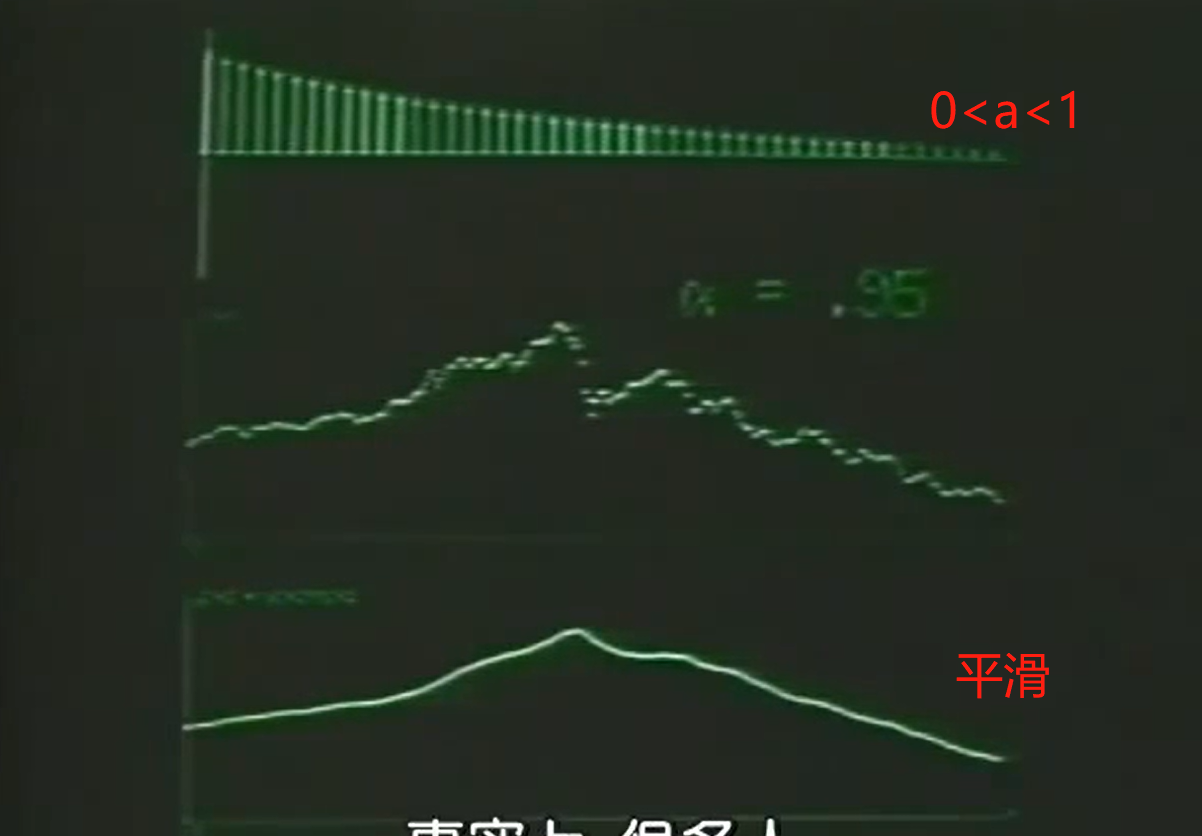
高通滤波更关注转折点/快速变化的地方
4 调制特性MODULATION PROPERTY
时域上信号乘积,则频域上表现为卷积 == 对时域信号处理,可以简洁调制频域信号

4.1 example:
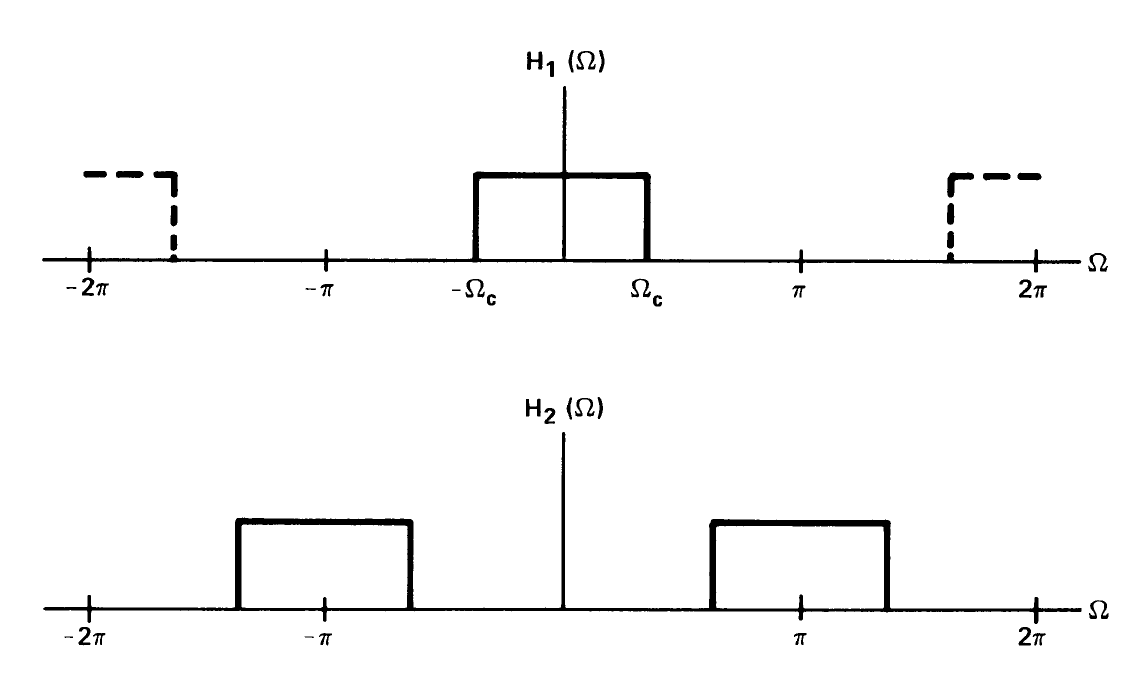
对于周期信号,其傅里叶变换为周期脉冲串,如下:
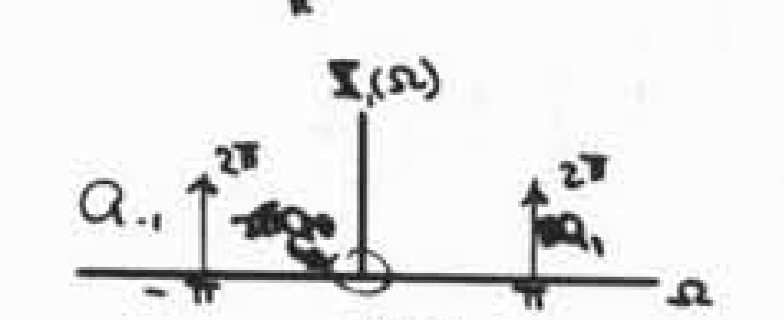
现在有一个信号,时域上将它乘上
,则其频域变化为频谱位移Π,低频部分变为高频。
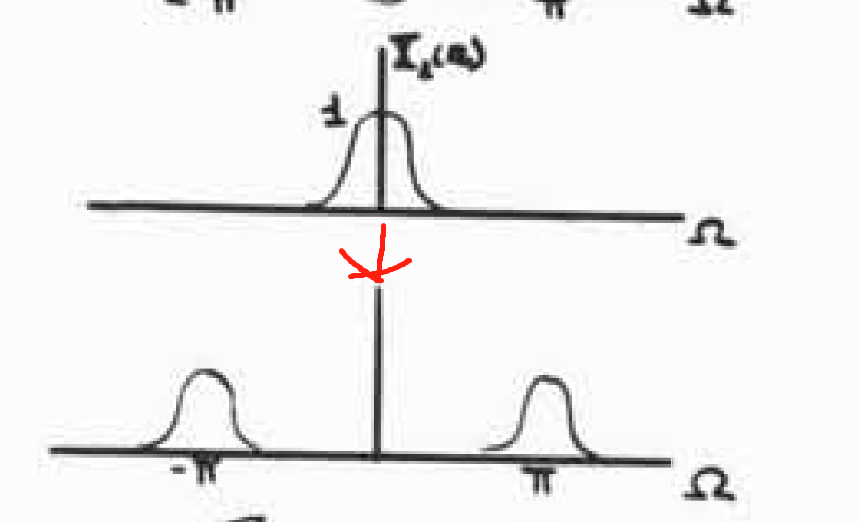
下图也是一个信号时域上将它乘上后频谱图位移的情形。
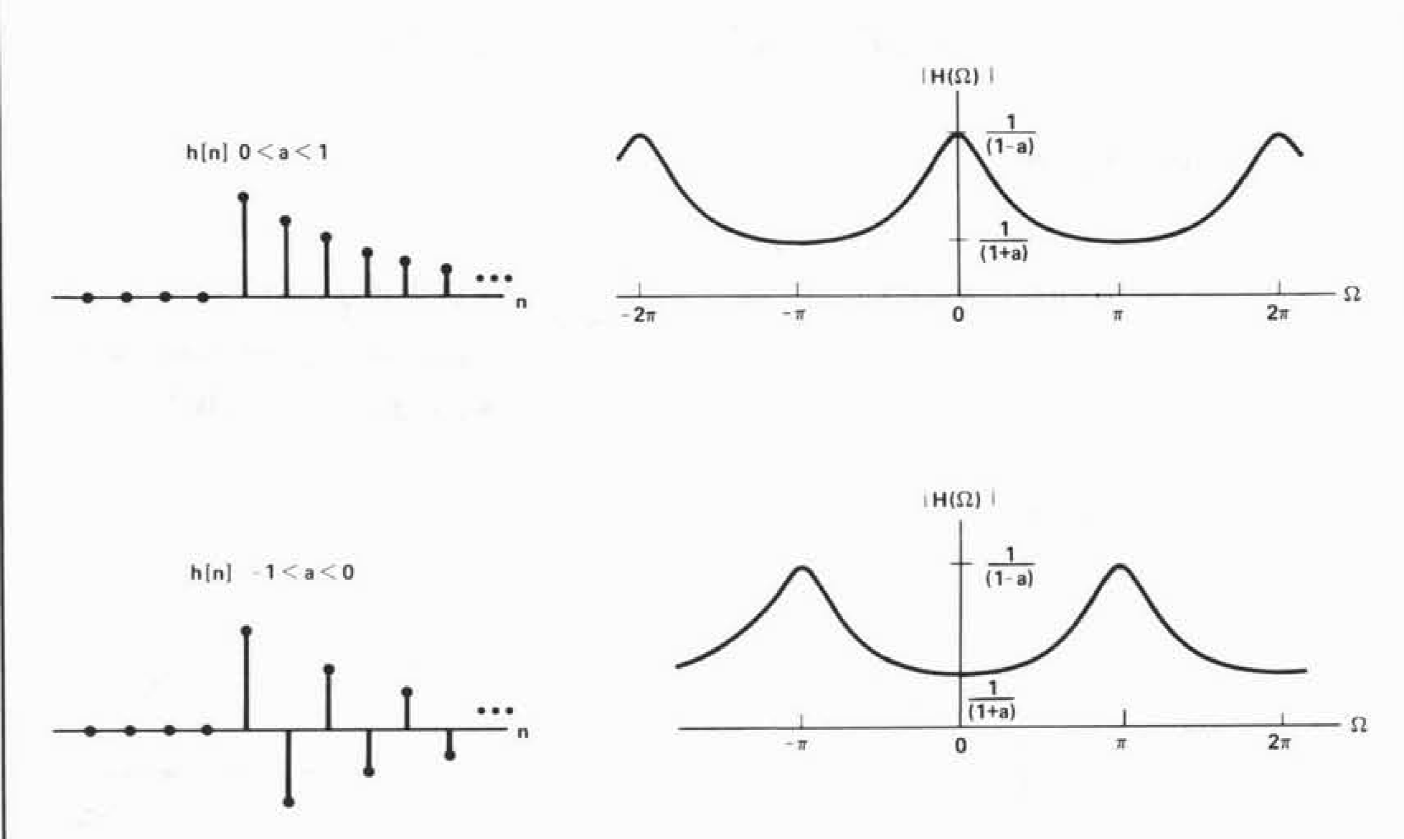
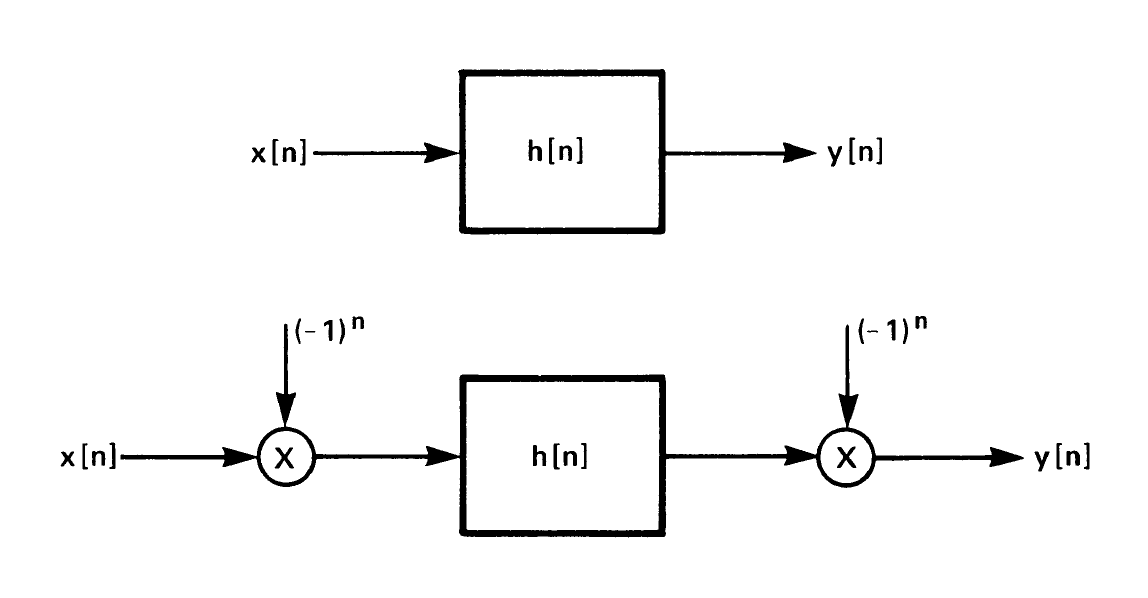
应用: ①可以将低通滤波器变为高通滤波器:低频和高频部分调换
★5 傅里叶分析总结
(yes or no指对偶性)