1 数据结构相关名词
先上一张图
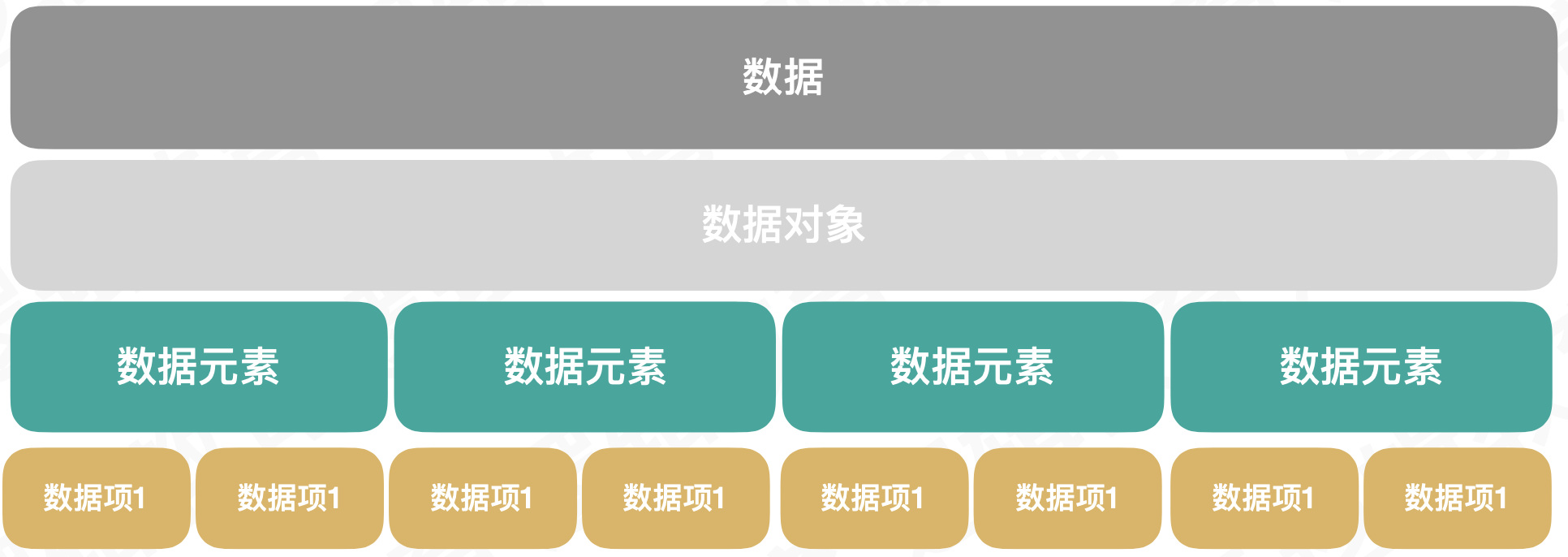
数据类型:
数据类型分为
和
2 逻辑结构与物理结构
- 逻辑结构:集合结构 线性结构 树形结构 图形结构
- 物理结构:顺序存储结构 链式存储结构
3 算法设计要求
- 正确性
- 可读性
- 健壮性
- 时间效率高和储存量低
4 算法效率衡量方法
时间复杂度和空间复杂度的概念引入
5 算法时间复杂度
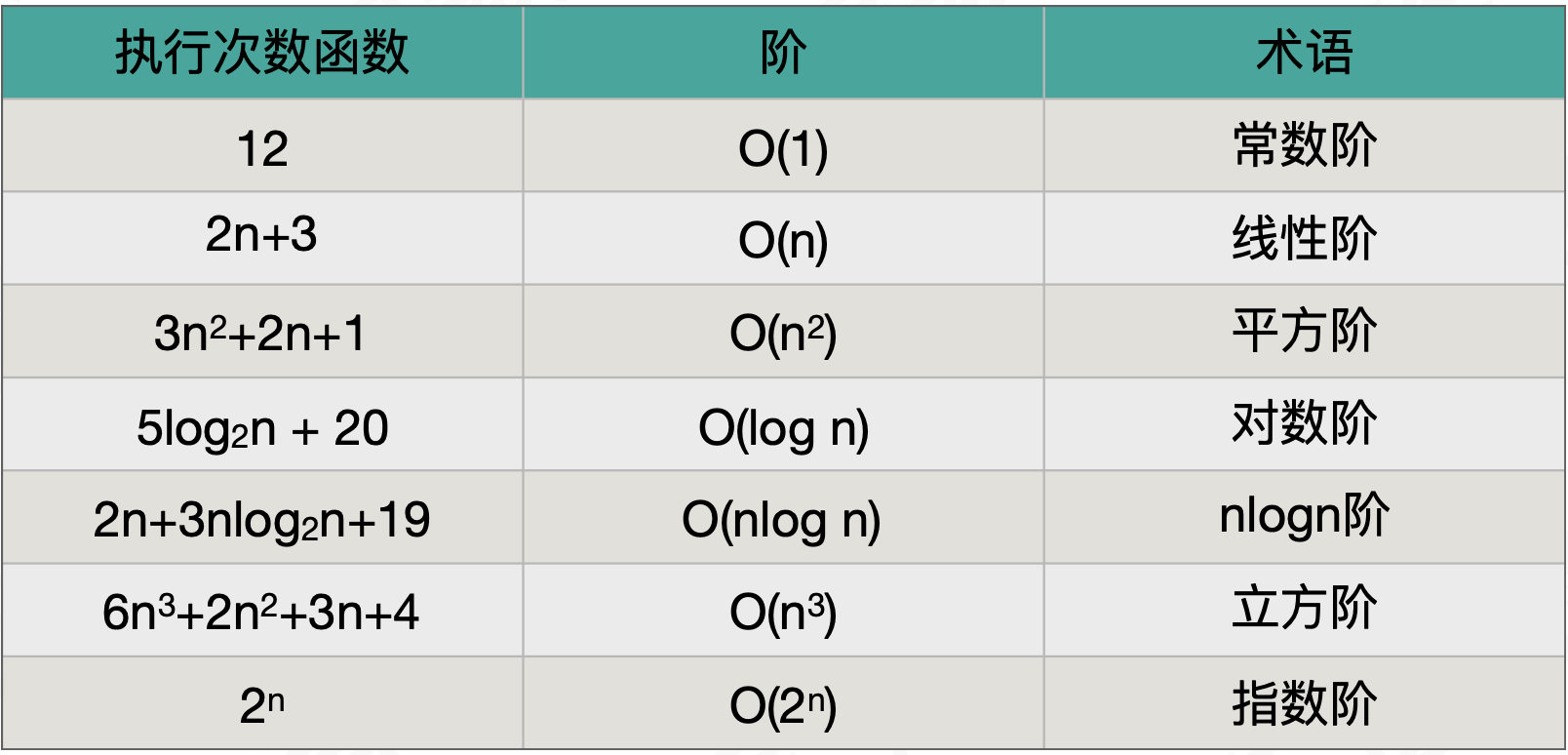
6 常见的时间复杂度
O(1) < O(log n) < O(n) < O(nlog n) < O(n2) < O(n3) < O(2n) < O(n!) < O(nn)
7 算法空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法空间复杂度的计算公式 记做: S(n) = n(f(n)),其中,n为问题的规模,f(n)为语句句关于n所占存储空间的函数
8 线性表 顺序存储的增删改查
首先要介绍线性表和线性结构的特点
- 存在唯一的一个被称作”第一个”的数据元素;
- 存在唯一的一个被称作”最后一个"的数据元素
- 除了了第一个之外,结构中的每个数据元素均有一个前驱
- 除了了最后一个之外,结构中的每个数据元素都有一个后继
//顺序表结构设计
typedef struct {
ElemType *data;
int length;
}Sqlist;
//1.1 顺序表初始化
Status InitList(Sqlist *L){
//为顺序表分配一个大小为MAXSIZE 的数组空间
L->data = malloc(sizeof(ElemType) * MAXSIZE);
//存储分配失败退出
if(!L->data) exit(ERROR);
//空表长度为0
L->length = 0;
return OK;
}
//1.2 顺序表的插入
/*
初始条件:顺序线性表L已存在,1≤i≤ListLength(L);
操作结果:在L中第i个位置之前插入新的数据元素e,L的长度加1
*/
Status ListInsert(Sqlist *L,int i,ElemType e){
//i值不合法判断
if((i<1) || (i>L->length+1)) return ERROR;
//存储空间已满
if(L->length == MAXSIZE) return ERROR;
//插入数据不在表尾,则先移动出空余位置
if(i <= L->length){
for(int j = L->length-1; j>=i-1;j--){
//插入位置以及之后的位置后移动1位
L->data[j+1] = L->data[j];
}
}
//将新元素e 放入第i个位置上
L->data[i-1] = e;
//长度+1;
++L->length;
return OK;
}
//1.3 顺序表的取值
Status GetElem(Sqlist L,int i, ElemType *e){
//判断i值是否合理, 若不合理,返回ERROR
if(i<1 || i > L.length) return ERROR;
//data[i-1]单元存储第i个数据元素.
*e = L.data[i-1];
return OK;
}
//1.4 顺序表删除
/*
初始条件:顺序线性表L已存在,1≤i≤ListLength(L)
操作结果: 删除L的第i个数据元素,L的长度减1
*/
Status ListDelete(Sqlist *L,int i){
//线性表为空
if(L->length == 0) return ERROR;
//i值不合法判断
if((i<1) || (i>L->length+1)) return ERROR;
for(int j = i; j < L->length;j++){
//被删除元素之后的元素向前移动
L->data[j-1] = L->data[j];
}
//表长度-1;
L->length --;
return OK;
}
9 线性表 单链表的增删改查以及头插法和尾插法
//定义结点
typedef struct Node{
ElemType data;
struct Node *next;
}Node;
typedef struct Node * LinkList;
初始化
//2.1 初始化单链表线性表
Status InitList(LinkList *L){
//产生头结点,并使用L指向此头结点
*L = (LinkList)malloc(sizeof(Node));
//存储空间分配失败
if(*L == NULL) return ERROR;
//将头结点的指针域置空
(*L)->next = NULL;
return OK;
}
增
//2.2 单链表插入
/*
初始条件:顺序线性表L已存在,1≤i≤ListLength(L);
操作结果:在L中第i个位置之后插入新的数据元素e,L的长度加1;
*/
Status ListInsert(LinkList *L,int i,ElemType e){
int j;
LinkList p,s;
p = *L;
j = 1;
//寻找第i-1个结点
while (p && j<i) {
p = p->next;
++j;
}
//第i个元素不存在
if(!p || j>i) return ERROR;
//生成新结点s
s = (LinkList)malloc(sizeof(Node));
//将e赋值给s的数值域
s->data = e;
//将p的后继结点赋值给s的后继
s->next = p->next;
//将s赋值给p的后继
p->next = s;
return OK;
}
删
//2.4 单链表删除元素
/*
初始条件:顺序线性表L已存在,1≤i≤ListLength(L)
操作结果:删除L的第i个数据元素,并用e返回其值,L的长度减1
*/
Status ListDelete(LinkList *L,int i,ElemType *e){
int j;
LinkList p,q;
p = (*L)->next;
j = 1;
//查找第i-1个结点,p指向该结点
while (p->next && j<(i-1)) {
p = p->next;
++j;
}
//当i>n 或者 i<1 时,删除位置不合理
if (!(p->next) || (j>i-1)) return ERROR;
//q指向要删除的结点
q = p->next;
//将q的后继赋值给p的后继
p->next = q->next;
//将q结点中的数据给e
*e = q->data;
//让系统回收此结点,释放内存;
free(q);
return OK;
}
//2.3 单链表取值
/*
初始条件: 顺序线性表L已存在,1≤i≤ListLength(L);
操作结果:用e返回L中第i个数据元素的值
*/
Status GetElem(LinkList L,int i,ElemType *e){
//j: 计数.
int j;
//声明结点p;
LinkList p;
//将结点p 指向链表L的第一个结点;
p = L->next;
//j计算=1;
j = 1;
//p不为空,且计算j不等于i,则循环继续
while (p && j<i) {
//p指向下一个结点
p = p->next;
++j;
}
//如果p为空或者j>i,则返回error
if(!p || j > i) return ERROR;
//e = p所指的结点的data
*e = p->data;
return OK;
}
前插法
//3.1 单链表前插入法
/* 随机产生n个元素值,建立带表头结点的单链线性表L(前插法)*/
void CreateListHead(LinkList *L, int n){
LinkList p;
//建立1个带头结点的单链表
*L = (LinkList)malloc(sizeof(Node));
(*L)->next = NULL;
//循环前插入随机数据
for(int i = 0; i < n;i++)
{
//生成新结点
p = (LinkList)malloc(sizeof(Node));
//i赋值给新结点的data
p->data = i;
//p->next = 头结点的L->next
p->next = (*L)->next;
//将结点P插入到头结点之后;
(*L)->next = p;
}
}
后插法
//3.2 单链表后插入法
/* 随机产生n个元素值,建立带表头结点的单链线性表L(后插法)*/
void CreateListTail(LinkList *L, int n){
LinkList p,r;
//建立1个带头结点的单链表
*L = (LinkList)malloc(sizeof(Node));
//r指向尾部的结点
r = *L;
for (int i=0; i<n; i++) {
//生成新结点
p = (Node *)malloc(sizeof(Node));
p->data = i;
//将表尾终端结点的指针指向新结点
r->next = p;
//将当前的新结点定义为表尾终端结点
r = p;
}
//将尾指针的next = null
r->next = NULL;
}
10 总结
线性表中的顺序表和单链表主要需要注意从第一个位置开始存储数据而不是从第0个;因为第0个数据需要做哨兵,避免插入和取值时额外的内存空间开销