天下武功, 无坚不破, 唯快不破 ——— 某功夫大佬

本文为我,leetcode easy player,algorithm小xuo生在刷题过程中对快慢指针的应用的总结

ps: 向leetcode里耐心写解题, 特别是画图解题的各位算法大佬们致敬, 给大佬们递茶🍵

什么是快慢指针

快慢说的是移动的速度, 即每次移动的步长的大小
指针为记录变量内存地址的变量, 用它能间接访问变量的值

为了更直观的了解快慢指针, 请看如下c++demo

在内存中开辟容量为11个整型元素的数组存储空间

初始化整型快慢指针变量都记录数组第一个元素的内存地址

在循环里, 慢指针每次增1, 快指针每次增2

因为c++中int占4字节即32位的16进制的内存空间, 所以慢指针记录的内存地址每次移动4个字节, 而快指针记录的内存地址每次移动8个字节( 注意因为是16进制, 所以快指针记录的内存地址从0x7ffee3c63258到0x7ffee3c63260也是移动了8个字节)

#include <iostream>
using namespace std;
int main (int argc, char const *argv[]) {
  int arr[11] = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };
  int *slowPointer = &arr[0];
  cout<<"slowPointer init point address: "<<slowPointer<<endl;
  int *fastPointer = &arr[0];
  cout<<"fastPointer init point address: "<<fastPointer<<endl;
  for (int i = 0; i < 5; ++i) {
    slowPointer++;
    fastPointer += 2;
    cout<<"i = "<<i<<endl;
    cout<<"slowPointer point address: "<<slowPointer<<endl;
    cout<<"slowPointer -> "<<*slowPointer<<endl;
    cout<<"fastPointer point address: "<<fastPointer<<endl;
    cout<<"fastPointer -> "<<*fastPointer<<endl;
  }
  return 0;
}

// slowPointer init point address: 0x7ffee3c63250
// fastPointer init point address: 0x7ffee3c63250
// i = 0
// slowPointer point address: 0x7ffee3c63254
// slowPointer -> 1
// fastPointer point address: 0x7ffee3c63258
// fastPointer -> 2
// i = 1
// slowPointer point address: 0x7ffee3c63258
// slowPointer -> 2
// fastPointer point address: 0x7ffee3c63260
// fastPointer -> 4
// i = 2
// slowPointer point address: 0x7ffee3c6325c
// slowPointer -> 3
// fastPointer point address: 0x7ffee3c63268
// fastPointer -> 6
// i = 3
// slowPointer point address: 0x7ffee3c63260
// slowPointer -> 4
// fastPointer point address: 0x7ffee3c63270
// fastPointer -> 8
// i = 4
// slowPointer point address: 0x7ffee3c63264
// slowPointer -> 5
// fastPointer point address: 0x7ffee3c63278
// fastPointer -> 10

说人话, 龟兔赛跑的故事大家都应该听过, 可以把乌龟🐢比作慢指针, 兔子🐇比作快指针, 下面来自前端灵魂画师的乌龟🐢和兔子🐇带你进入快慢指针的应用场景

判断链表是否有环

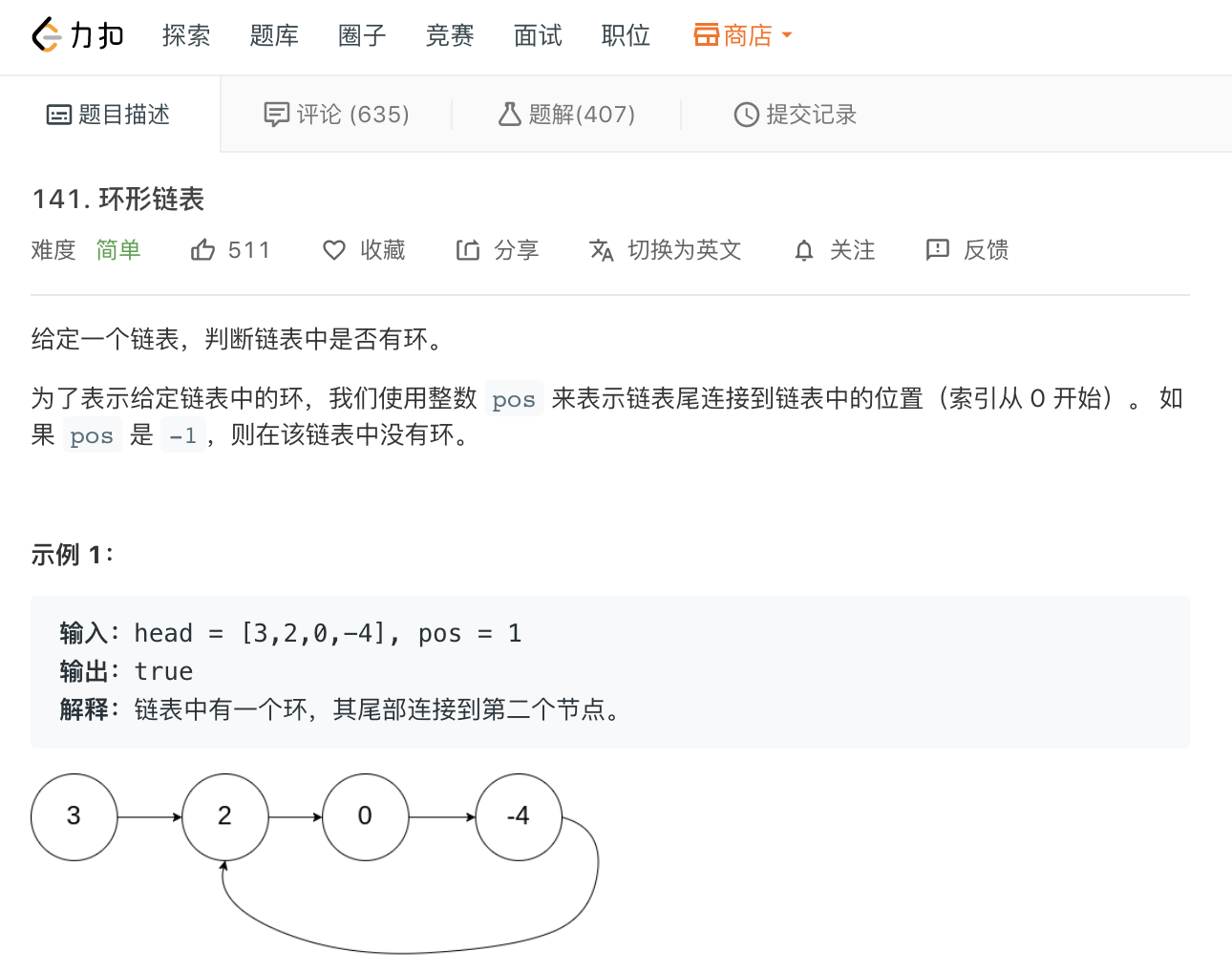
无环的链表是长这样的

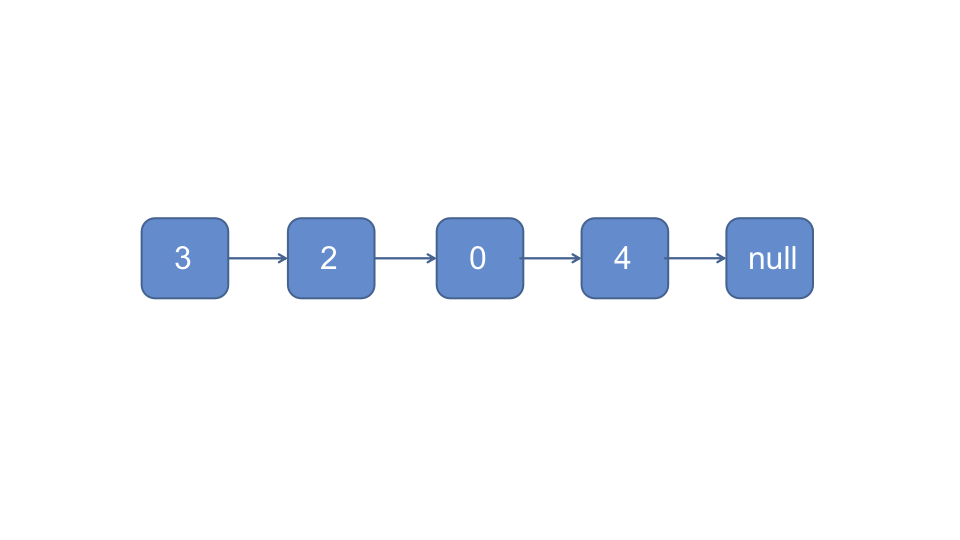
有环的链表是长这样的

染色标记法, 缺点: 改变了链表的结构, 若链表为只可读的则不可取, 而且此方法需开辟额外的O(n)存储空间记录标记信息

var hasCycle = function(head) {
  let res = false
  while (head && head.next) {
    if (head.flag) {
      res = true
      break
    } else {
      head.flag = 1
      head = head.next
    }
  }
  return res
};

哈希表记录法, 缺点: 哈希表需开辟额外的O(n)空间

var hasCycle = function(head) {
  const map = new Map()
  while (head) {
    if (map.get(head)) {
      return true
    } else {
      map.set(head, head)
      head = head.next
    }
  }
  return false
}

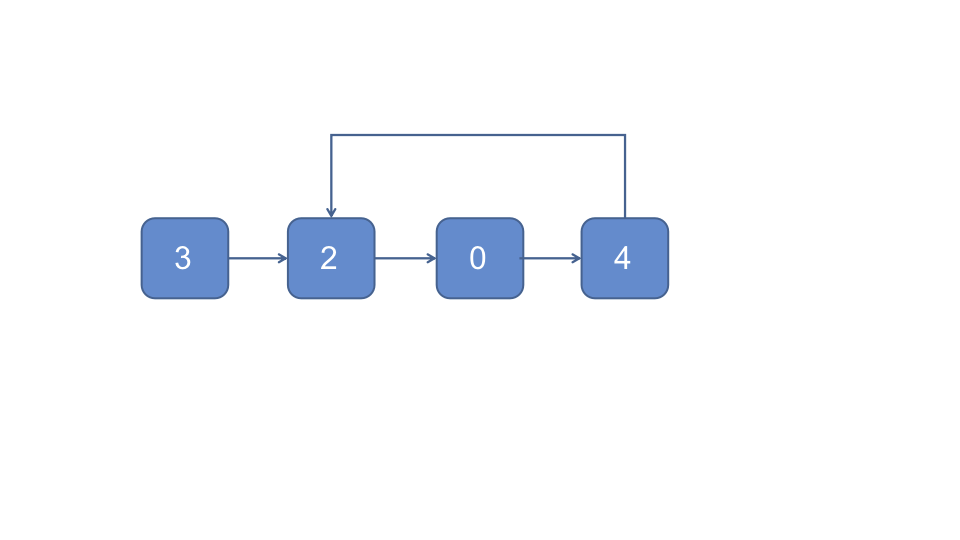
快慢指针法, 兔子与乌龟同时在头节点出发, 兔子每次跑两个节点, 乌龟每次跑一个节点, 如果兔子能够追赶到乌龟, 则链表是有环的

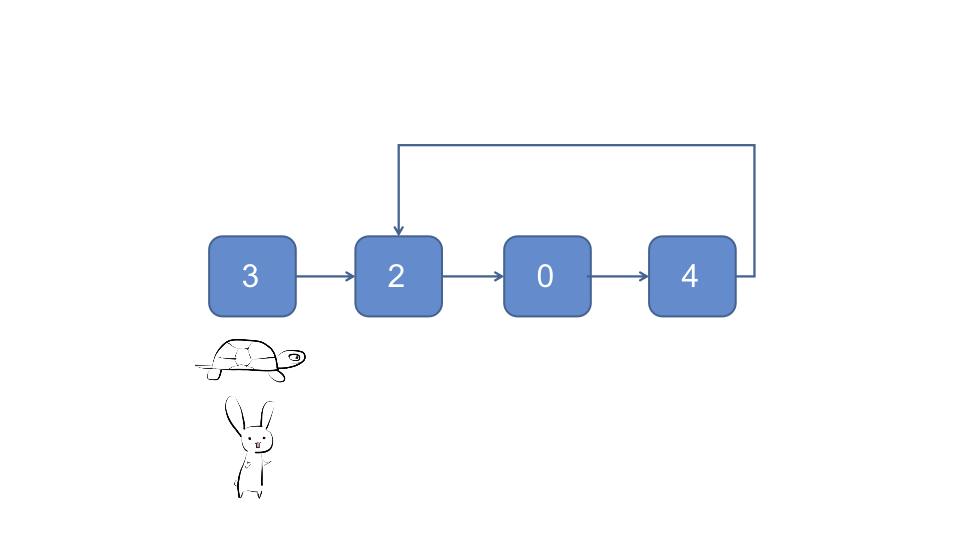
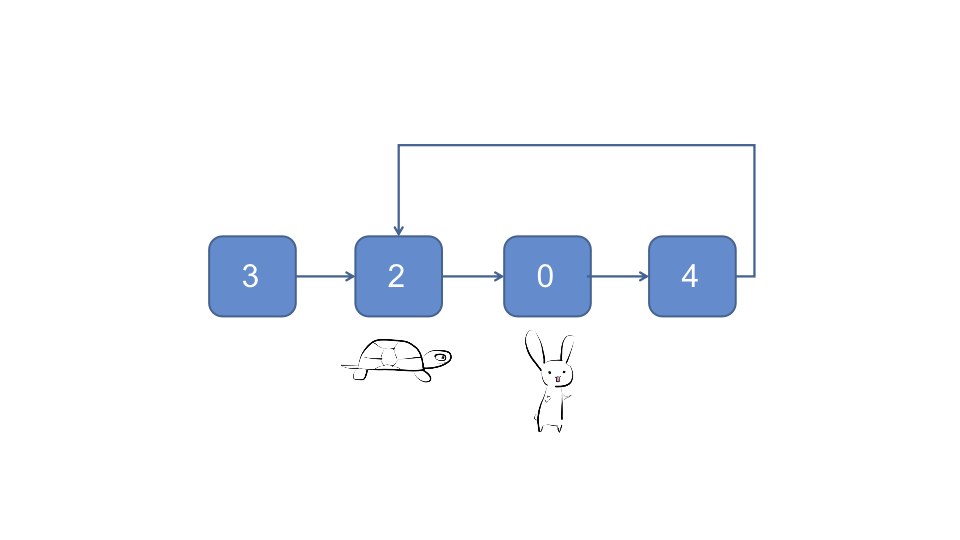
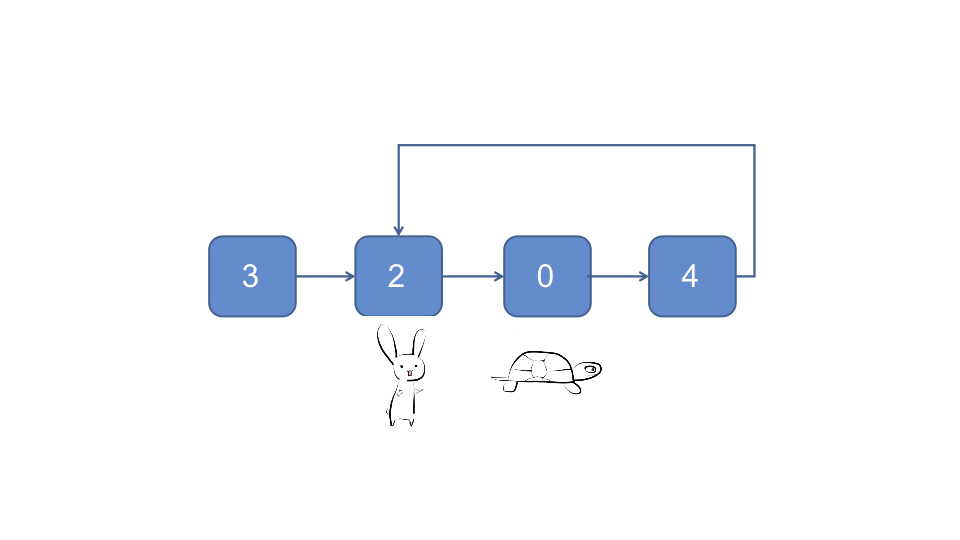
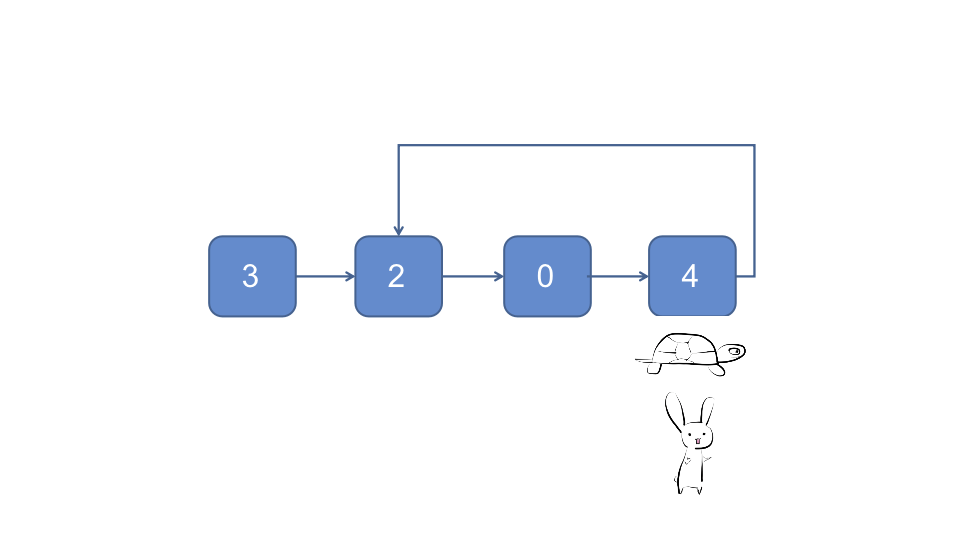
因为不管有没有环, 以及进环前和进换后耗时都与数据规模成正比, 所以时间复杂度为O(n), 因为只需额外的常数级存储空间记录两个指针, 所以空间复杂度为O(1)

var hasCycle = function(head) {
  let slowPointer = head
  let fastPointer = head
  while (fastPointer && fastPointer.next) {
    slowPointer = slowPointer.next
    fastPointer = fastPointer.next.next
    if (fastPointer === slowPointer) {
      return true
    }
  }
  return false
}

寻找链表的入环节点

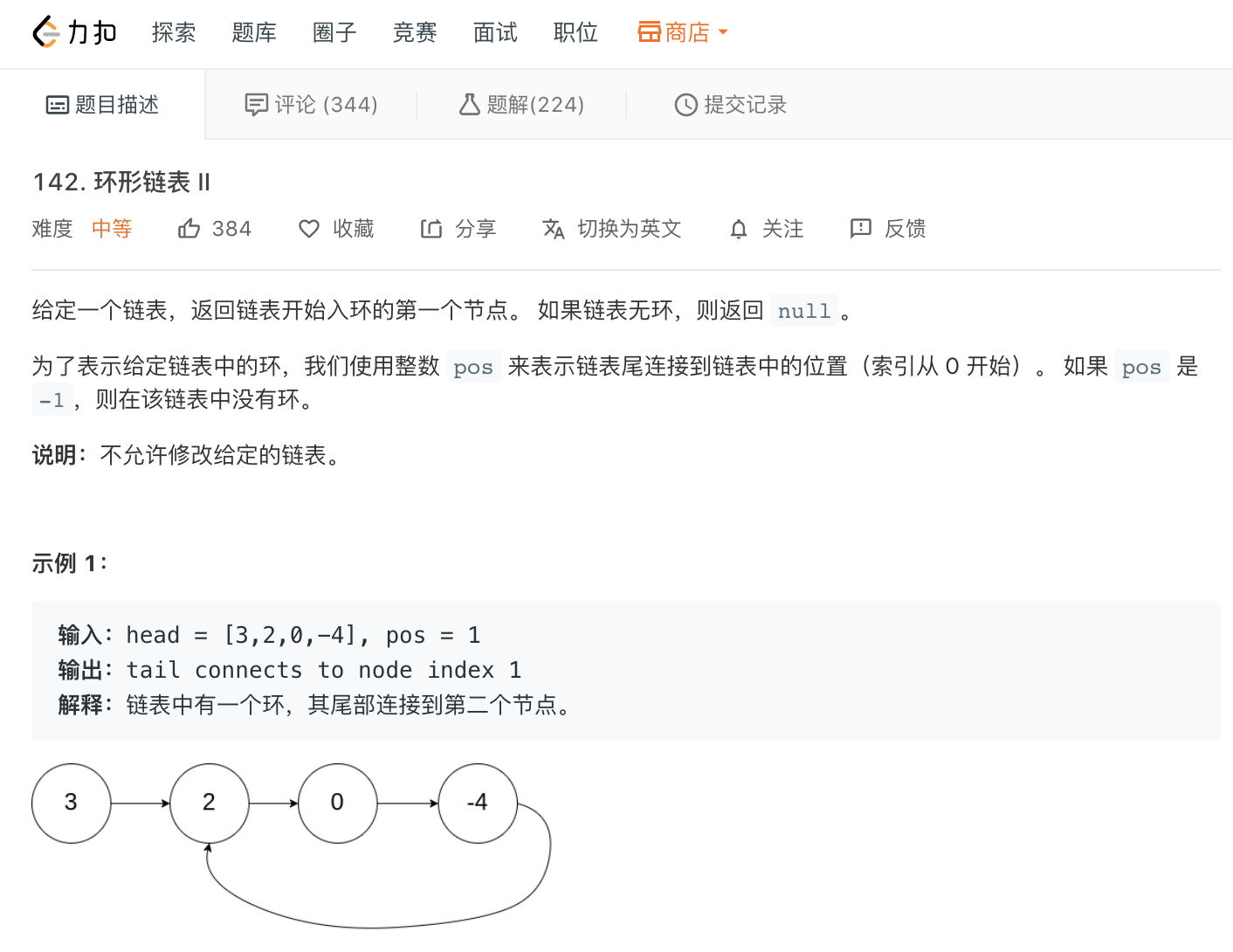
此题也可用标记法和哈希表法解决, 用快慢指针法解决如下

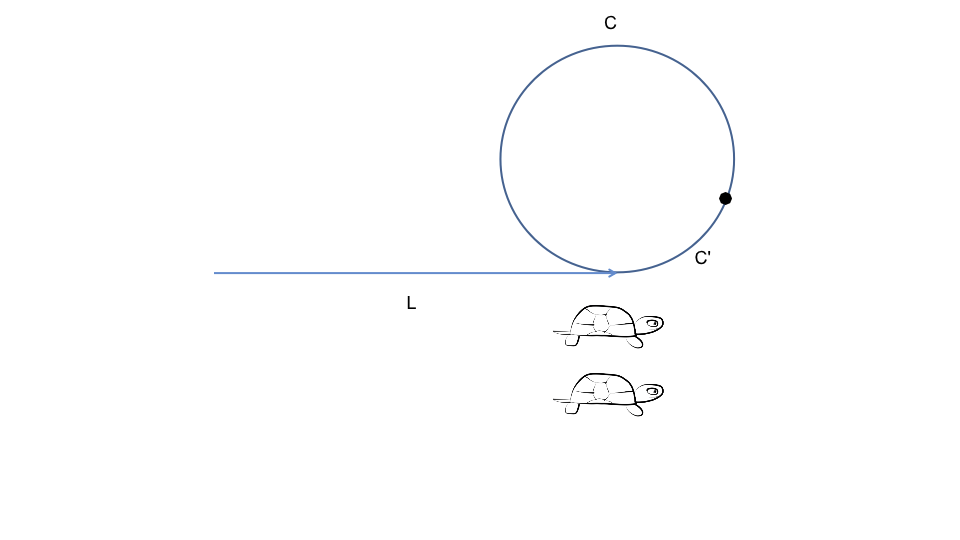
还是前面的龟兔赛跑, 当兔子追到乌龟的时候, 假设有另外一只乌龟从头节点开始往前爬, 每次也只爬一个节点, 那么两只乌龟会在入环的节点相遇

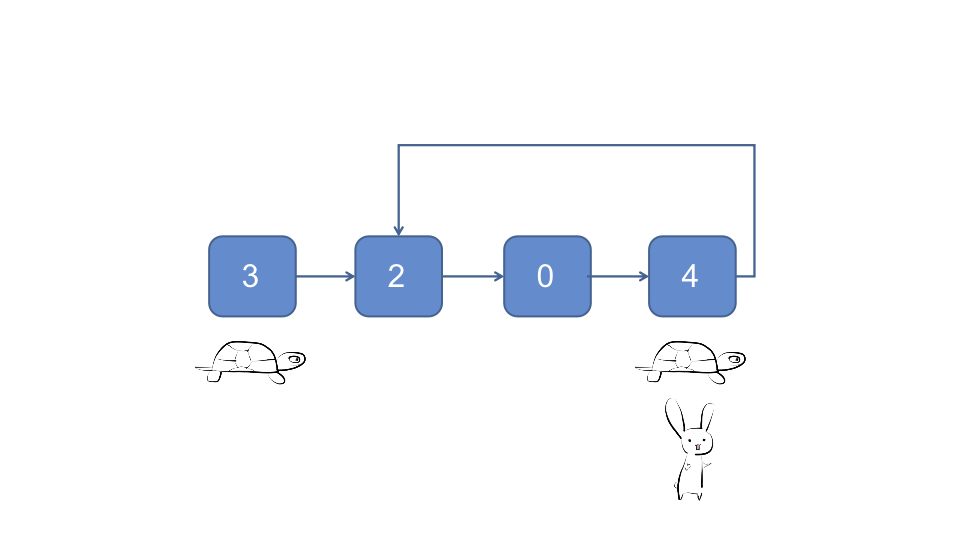
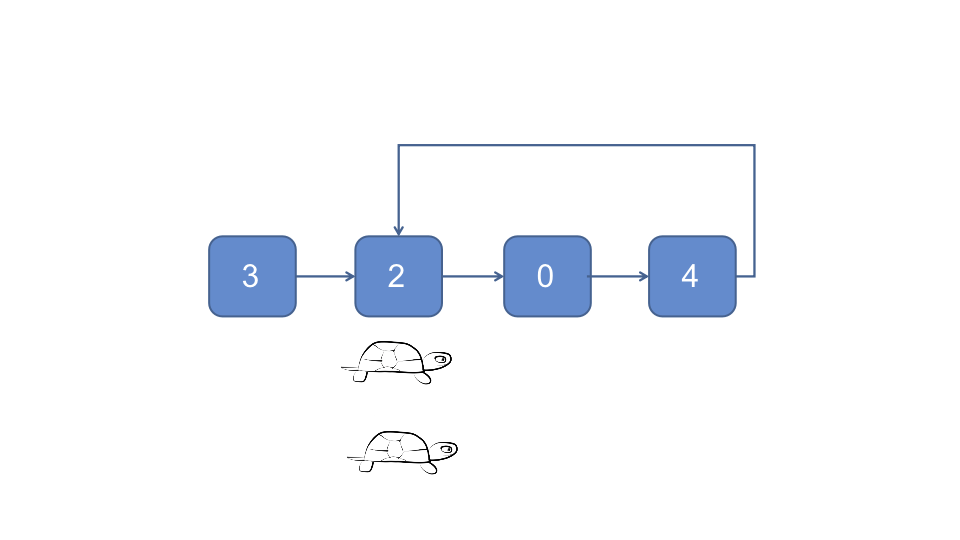
这只是一个巧合吗, 我们来分析一下

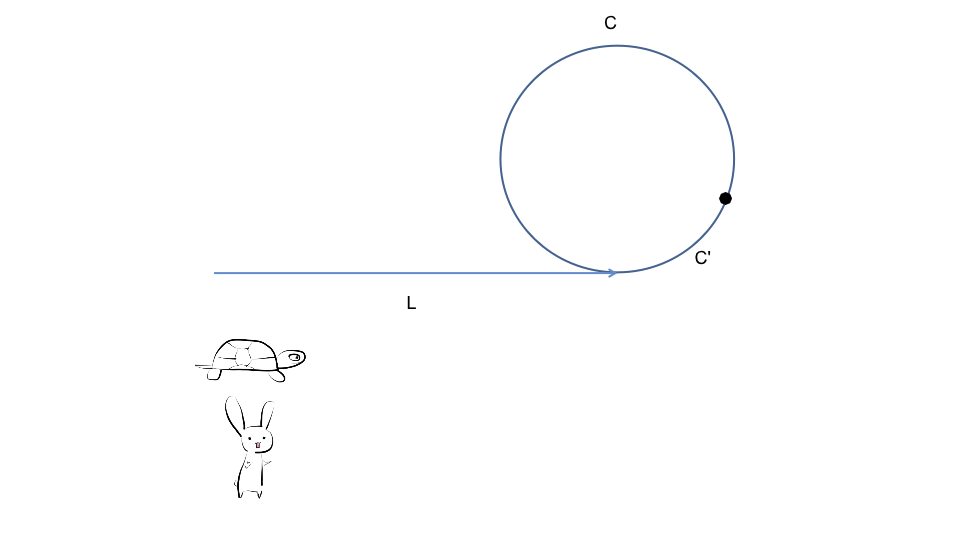
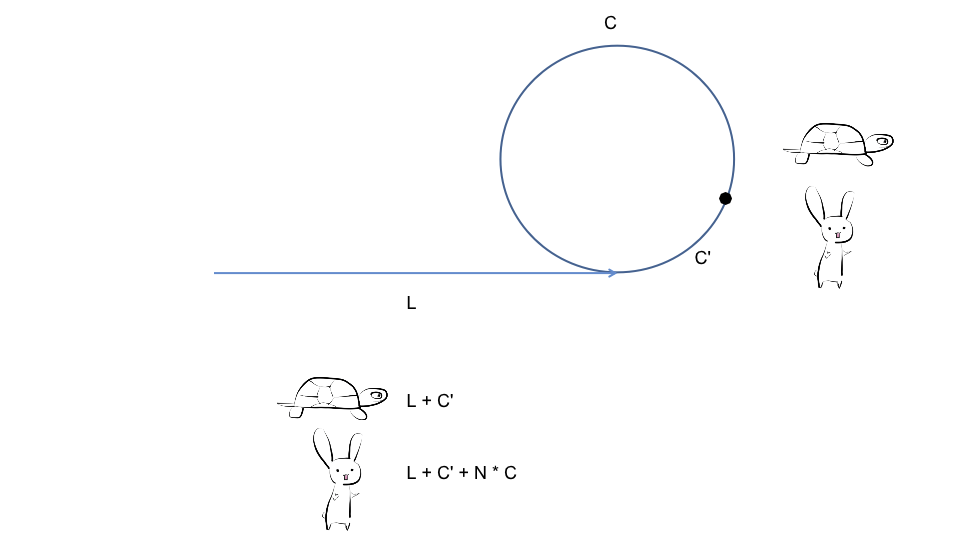
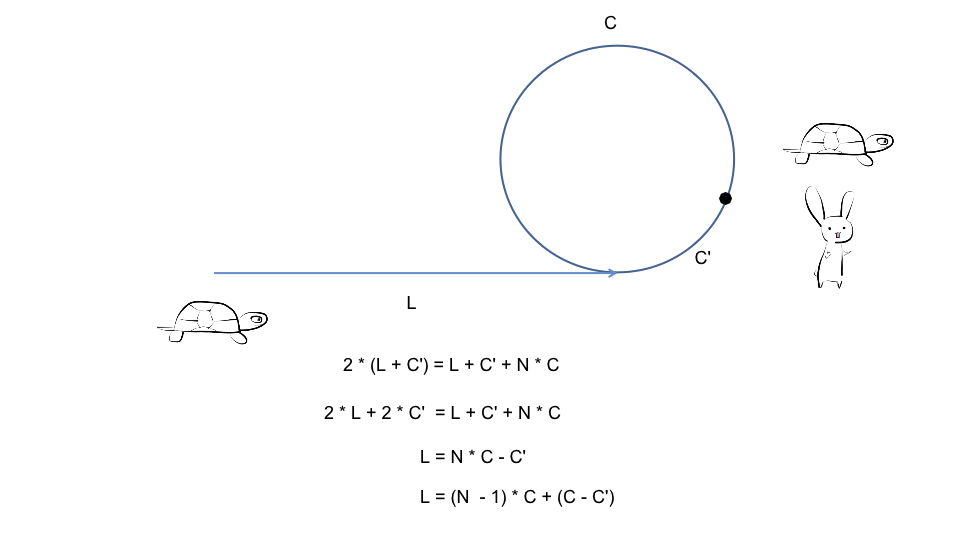
假设入环之前的长度为L, 入环之后快慢指针第一相遇时快指针比慢指针🐢多跑了N圈, 每一圈的长度为C, 此时快指针🐰在环内离入环节点的距离为C'
此时慢指针🐢走过的距离为: L + C'
此时快指针🐰走过的距离为: L + C' + N * C
因为快指针🐰的速度是慢指针🐢的两倍, 所以有: 2 * (L + C') = L + C' + N * C
整理后得到: (N - 1) * C + (C - C') = L
由此可知, 若此时有两个慢指针🐢同时分别从链表头结点和快慢指针第一次相遇的节点出发, 两者必然会在入环节点相遇

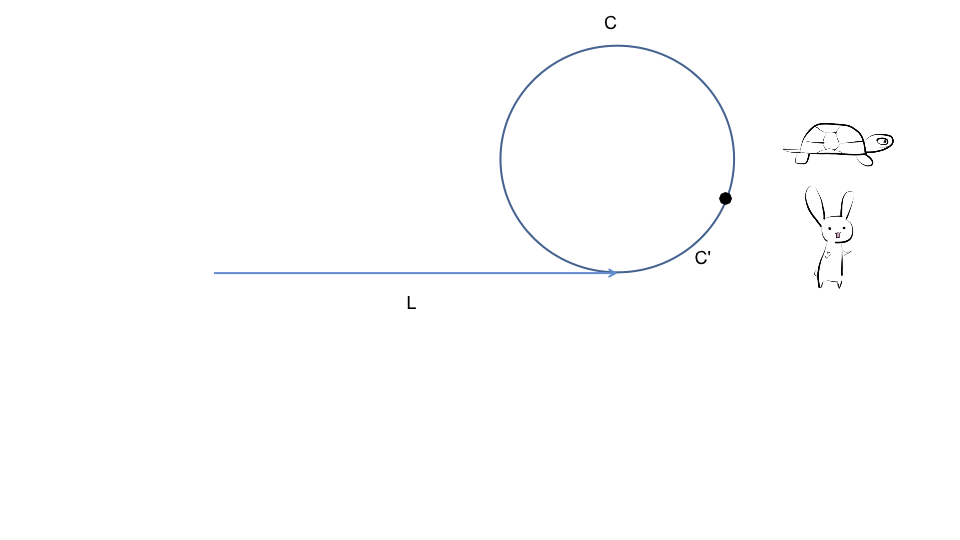
var detectCycle = function(head) {
  let slowPointer = head
  let fastPointer = head
  while (fastPointer && fastPointer.next) {
    slowPointer = slowPointer.next
    fastPointer = fastPointer.next.next
    if (slowPointer === fastPointer) {
      slowPointer = head
      while (slowPointer !== fastPointer) {
        slowPointer = slowPointer.next
        fastPointer = fastPointer.next
      }
      return slowPointer
    }
  }
  return null
};

寻找重复数

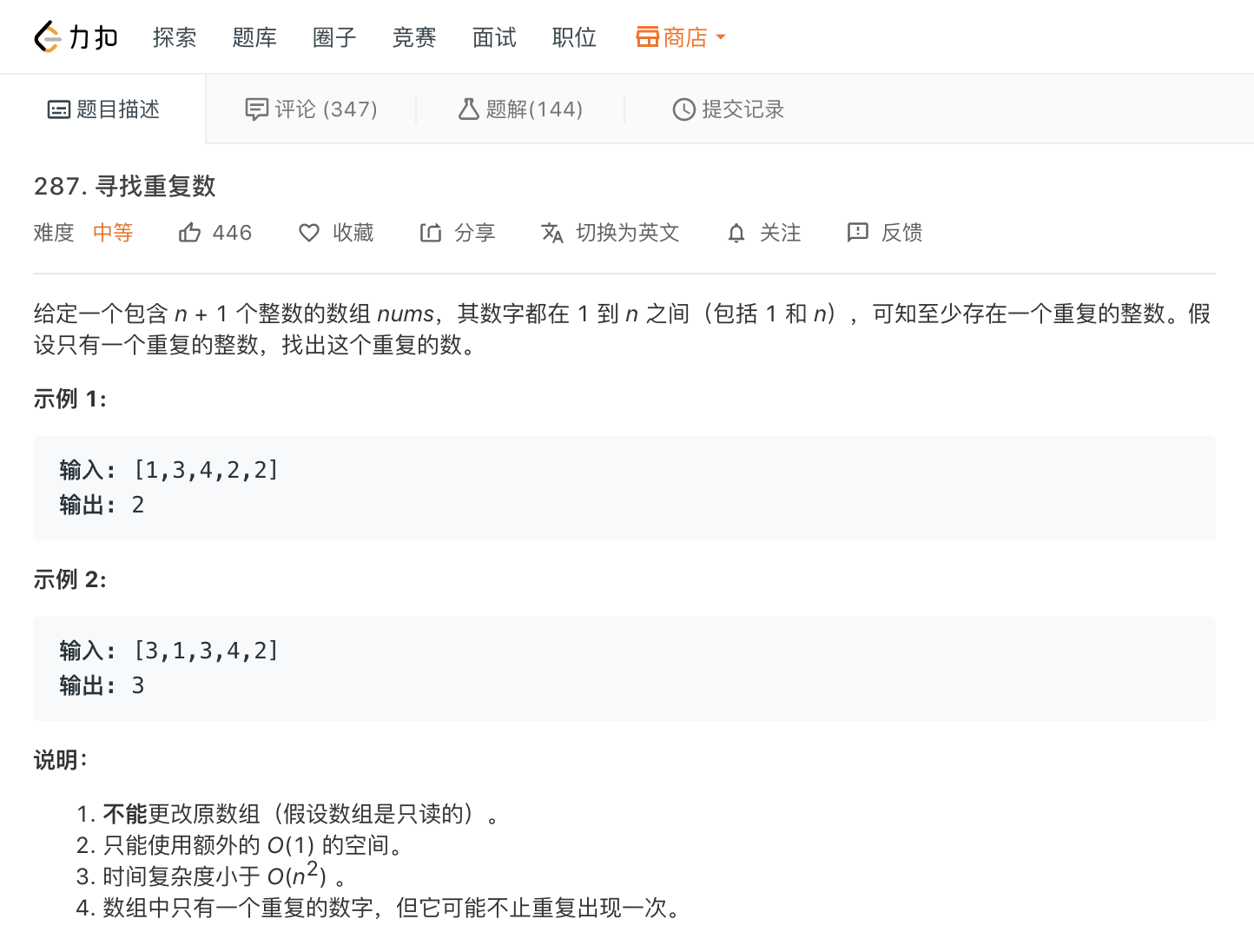
此题暴力解法为先排序再寻找重复的数字, 注意不同JavaScript引擎对sort的实现原理不一样, V8 引擎 sort 函数对数组长度小于等于 10 的用插入排序(时间复杂度O(n^2), 空间复杂度O(1))，其它的用快速排序(时间复杂度O(nlogn), 递归栈空间复杂度O(logn)), 参考github.com/v8/v8/blob/…

这一题可以利用寻找链表的入环节点的思想, 把数组当成对链表的一种描述, 数组里的每一个元素的值表示链表的下一个节点的索引

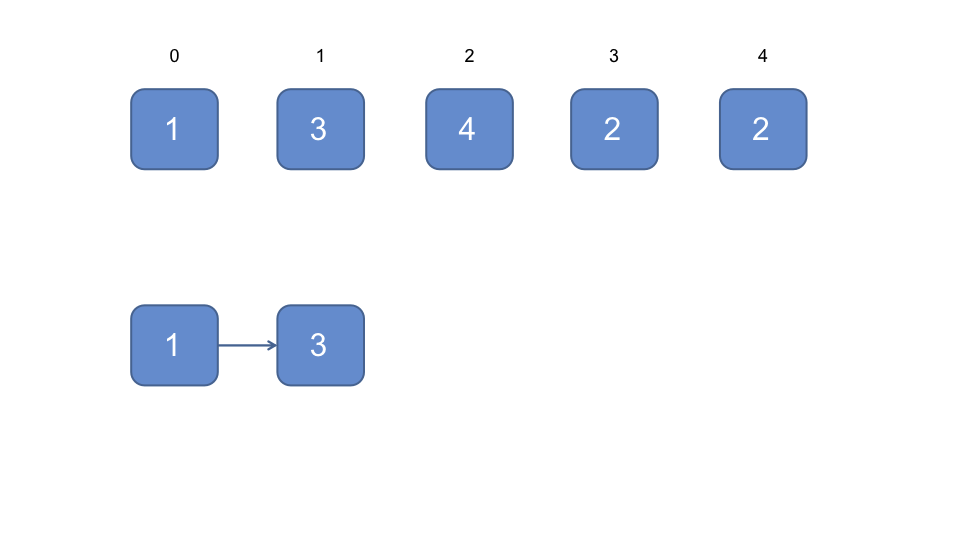
如示例1中的[1, 3, 4, 2, 2]

把数组索引为0的元素当成链表的头节点
索引为0的元素的值为1, 表示头节点的下一个节点的索引为1, 即数组中的3
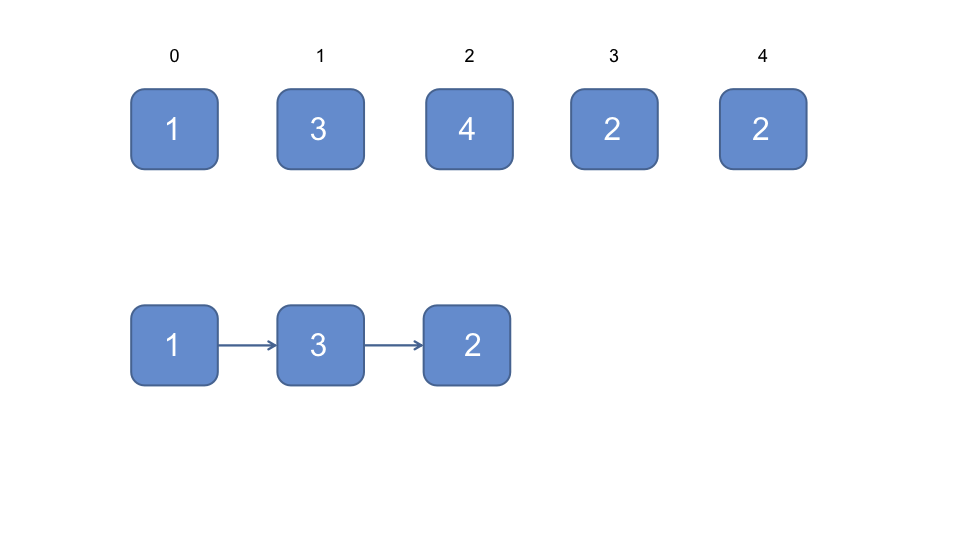
再下一个节点的索引为3, 即为第一个2
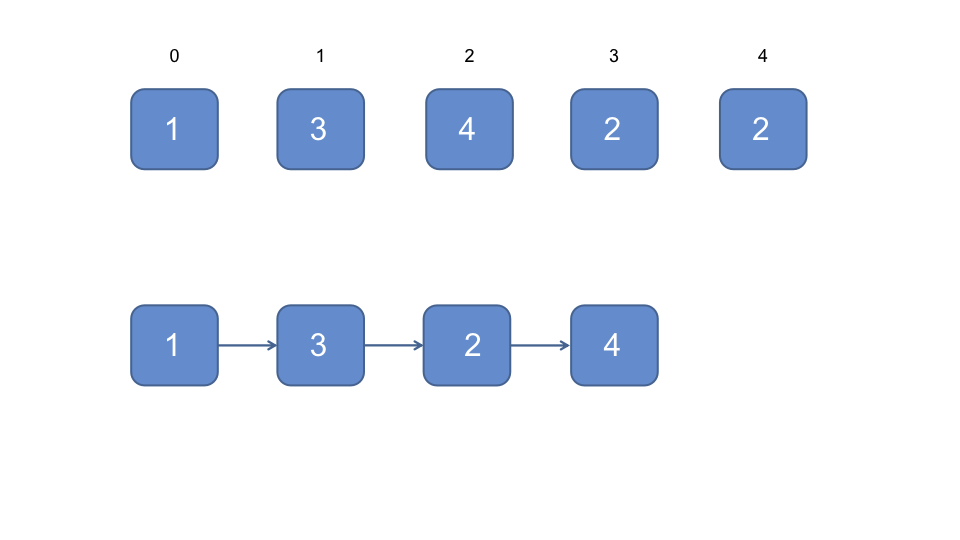
再下一个节点的索引为2, 即为4
再下一个节点的索引为4, 即为第二个2
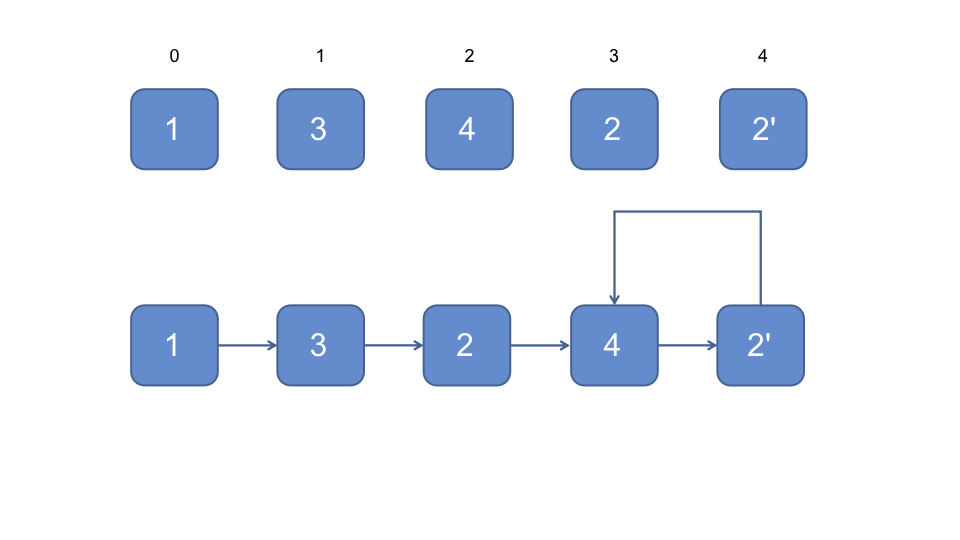
再下一个节点的索引为2, 即为4
此时形成了一个环
而形成环的原因是下一节点的索引一致, 即为重复的数字

var findDuplicate = function(nums) {
  let slowPointer = 0
  let fastPointer = 0
  while (true) {
    slowPointer = nums[slowPointer]
    fastPointer = nums[nums[fastPointer]]
    if (slowPointer == fastPointer) {
      let _slowPointer = 0
      while (nums[_slowPointer] !== nums[slowPointer]) {
        slowPointer = nums[slowPointer]
        _slowPointer = nums[_slowPointer]
      }
      return nums[_slowPointer]
    }
  }
};

删除链表的倒数第N个元素

要删除链表的倒数第N个元素, 需要找到其倒数第N + 1个元素, 让这个元素的next指向它的下下一个节点

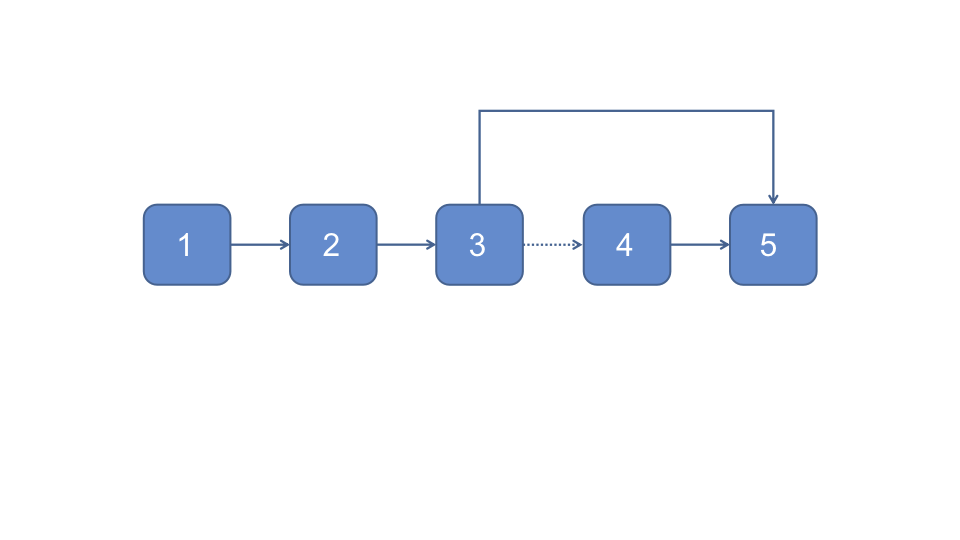
此题可利用两次正向遍历链表, 或者一次正向遍历的同时记录前节点, 然后再反向遍历

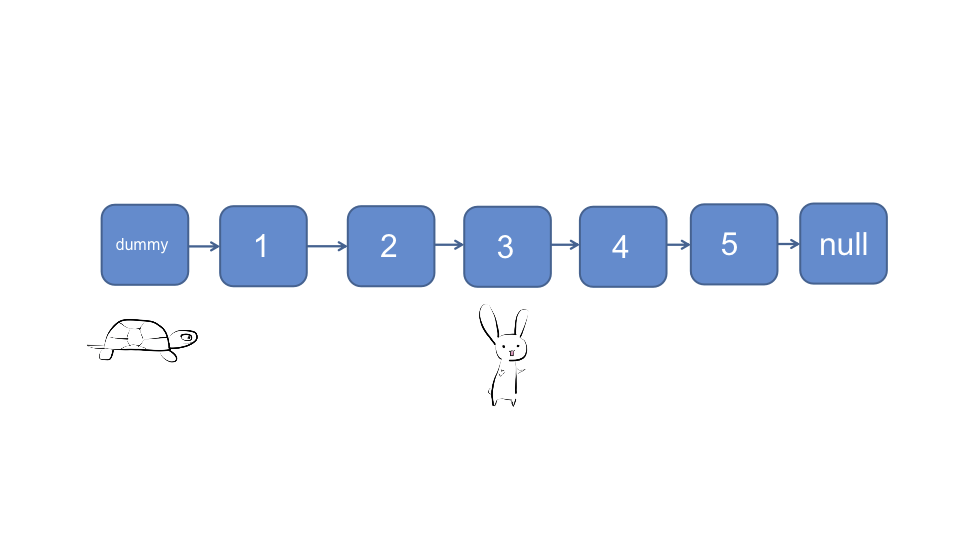
题目的进阶要求只使用一趟扫描, 利用快慢指针可实现, 我们最终想要的乌龟和兔子的位置是这样的, 它们之间相距N + 1个节点, 这样乌龟所在的位置即为我们想要找的那个节点--被删除的节点前面的一个节点

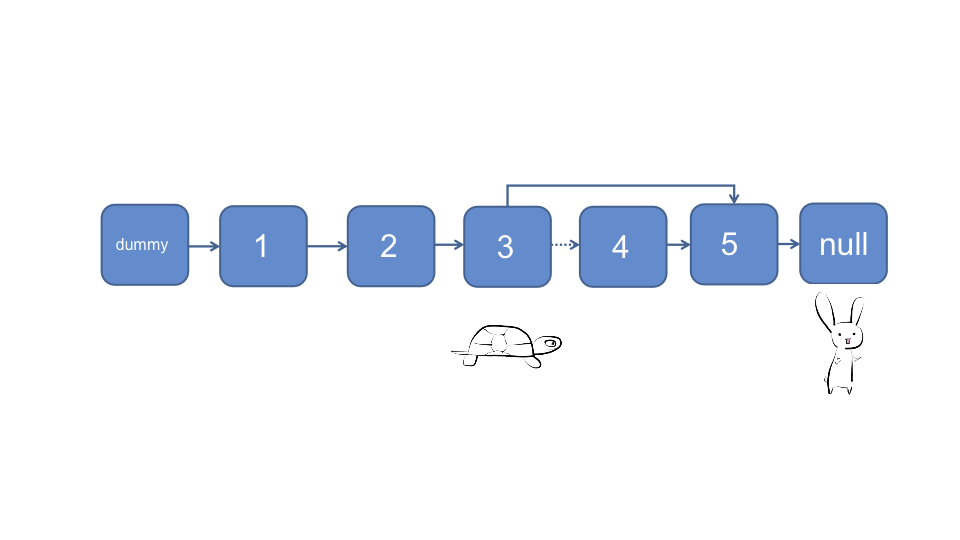
为方便处理头节点, 我们创建dummy虚拟头节点

让快指针🐰和慢指针🐰最开始都指向dummy节点

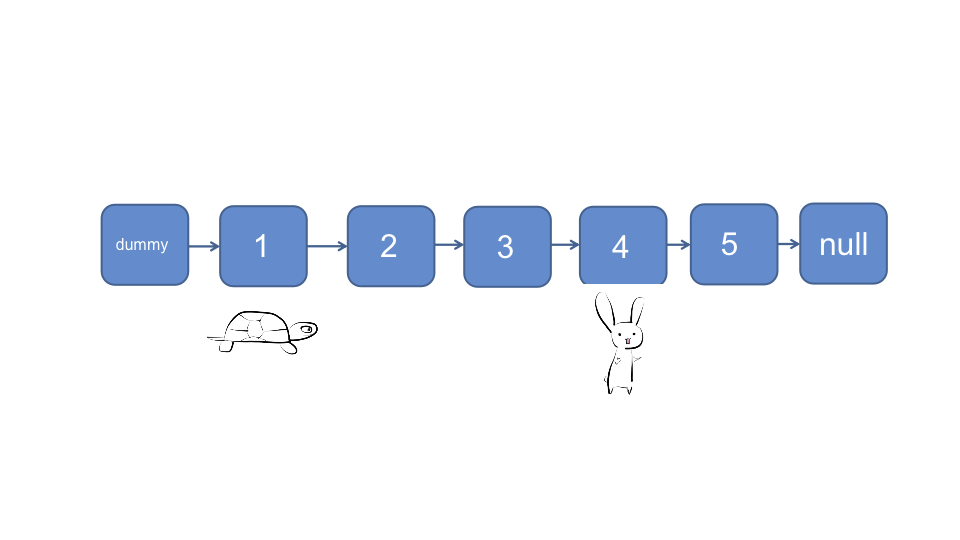
让快指针🐰向前移动N + 1个节点, 慢指针保持原地不动

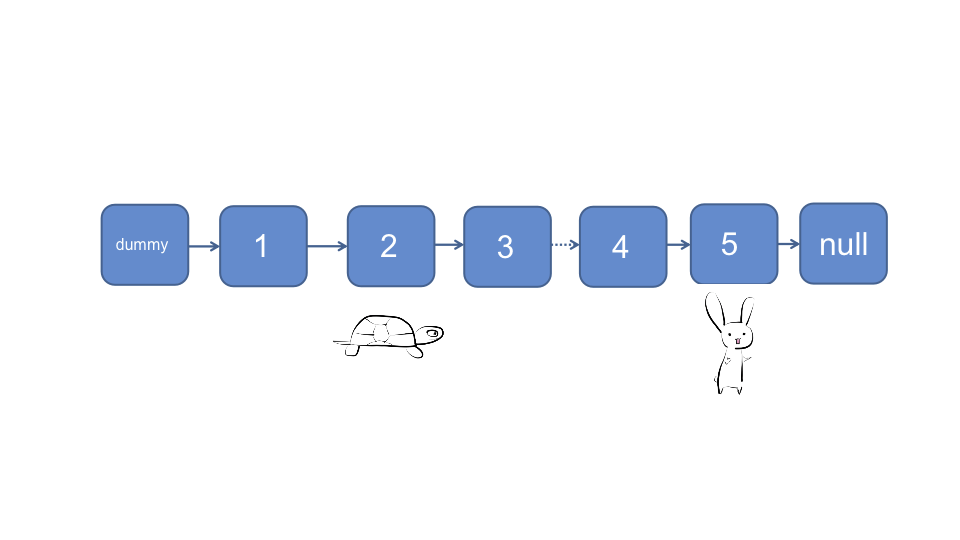
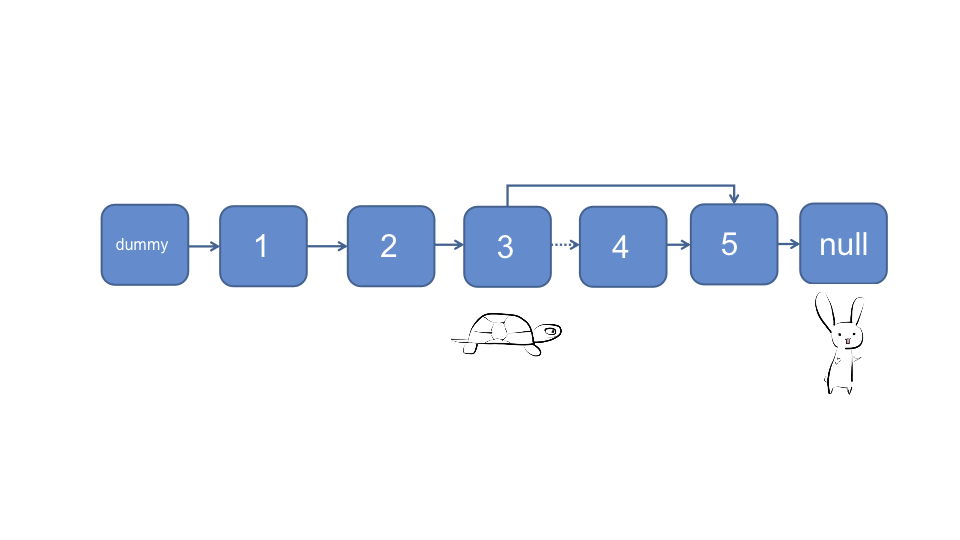
然后两个指针以同样的速度直至快指针🐰移动至null

此时慢指针🐢移动到的位置即为被删除的指针前面的一个指针

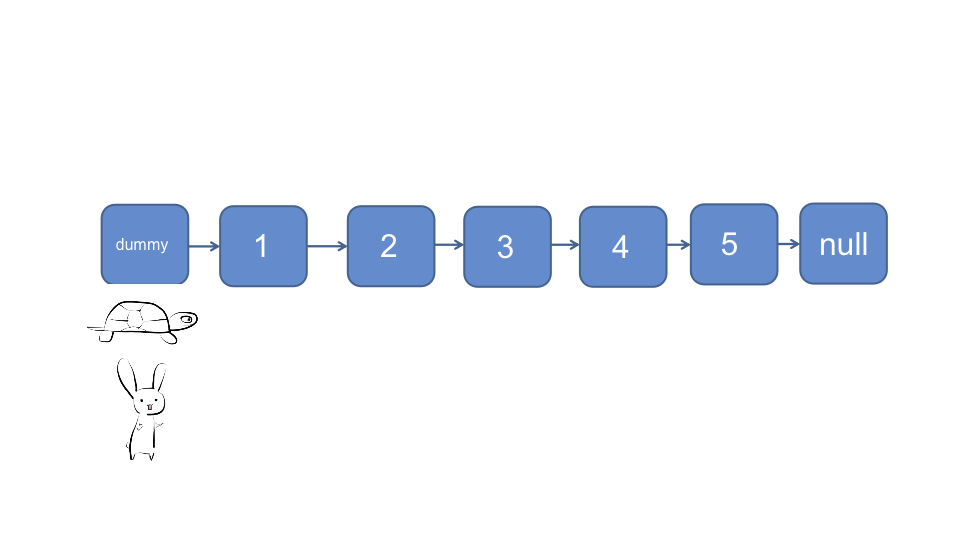
var removeNthFromEnd = function(head, n) {
  const dummy = new ListNode(null)
  dummy.next = head
  let slowPointer = dummy
  let fastPointer = dummy
  while (n-- > -1) {
    fastPointer = fastPointer.next
  }
  while (fastPointer !== null) {
    slowPointer = slowPointer.next
    fastPointer = fastPointer.next
  }
  slowPointer.next = slowPointer.next.next
  return slowPointer === dummy ? slowPointer.next : head
};

链表的中间节点

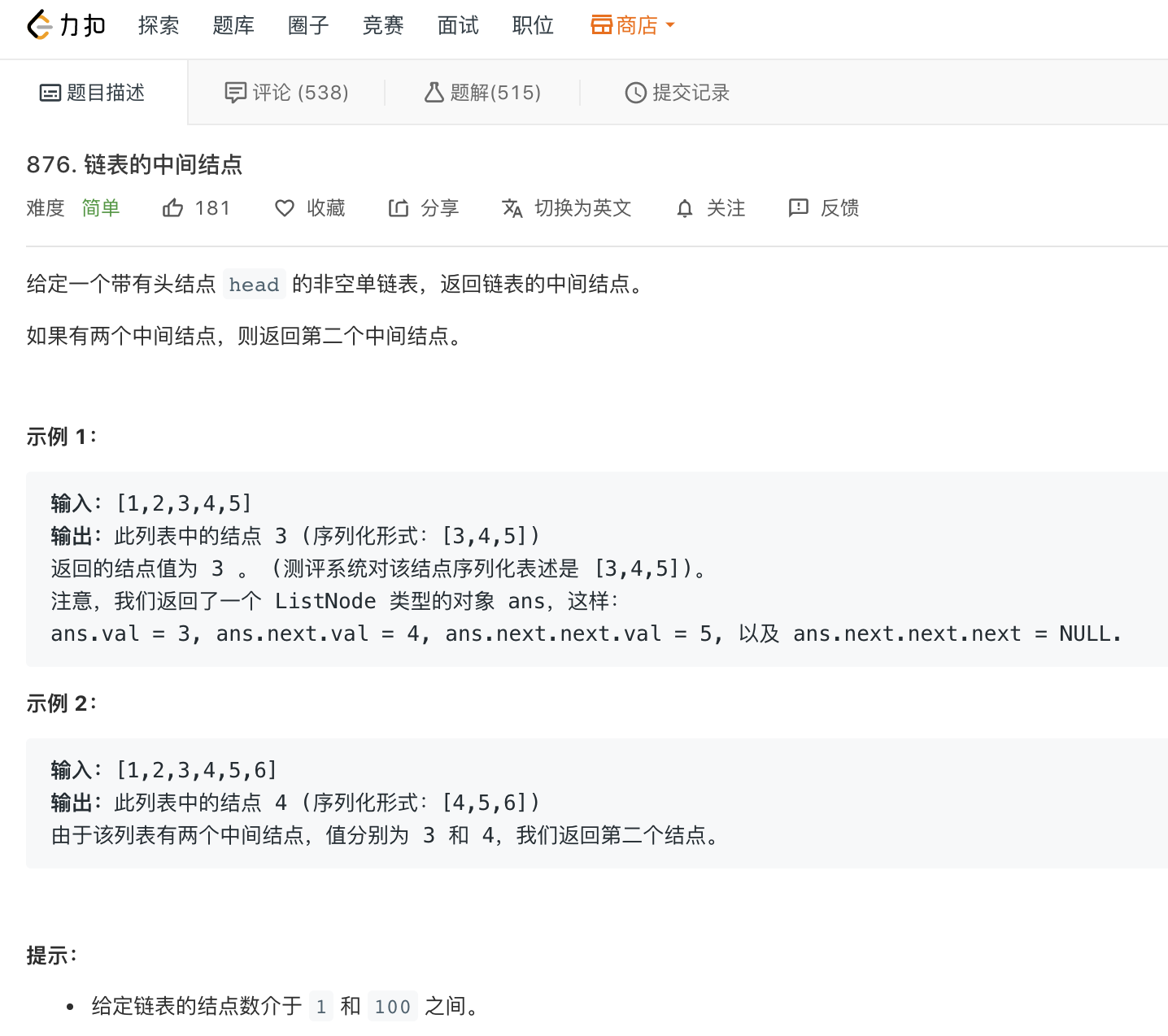
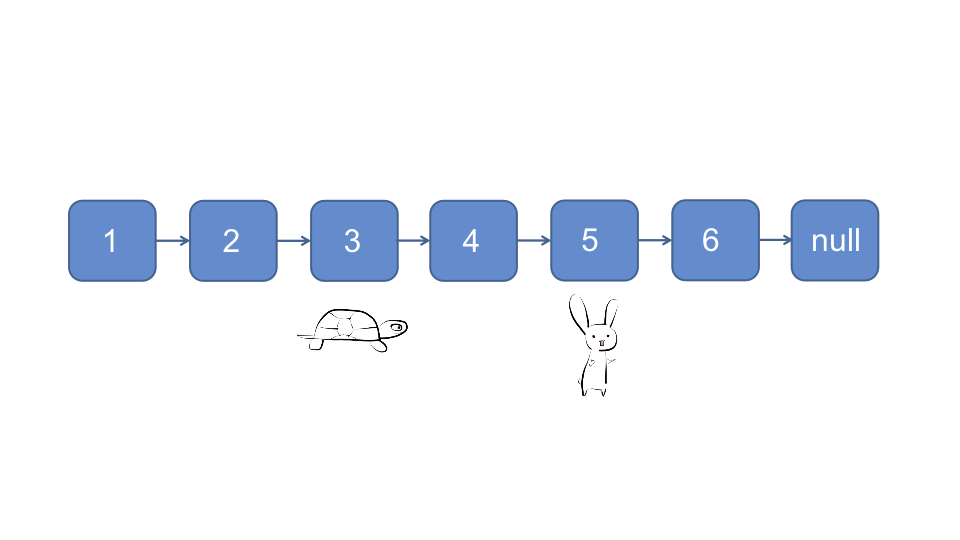
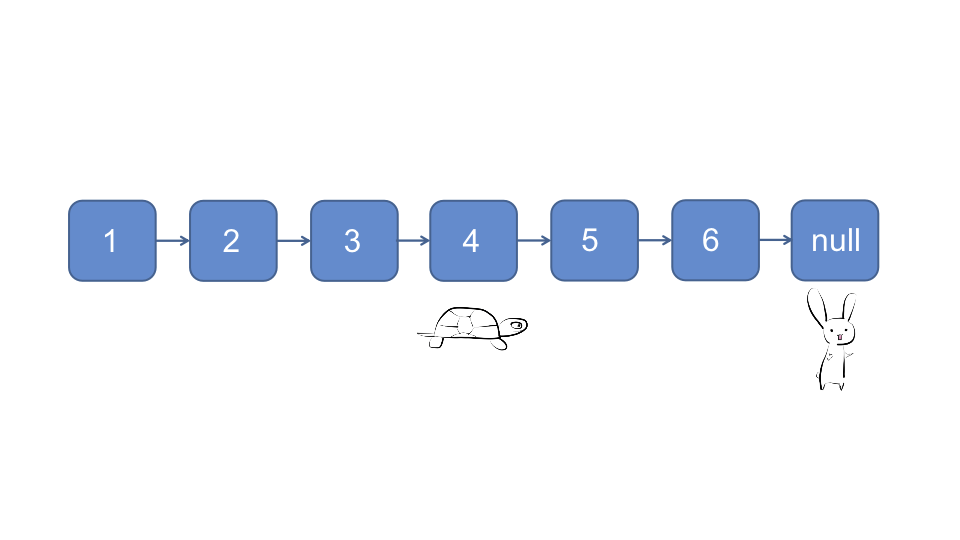
快慢指针法, 快慢指针开始时都指向头节点, 快指针每次移动一个节点, 慢指针每次移动两个节点

对于奇数链表, 当快指针下一节点为null时, 慢指针指向的节点即为所求

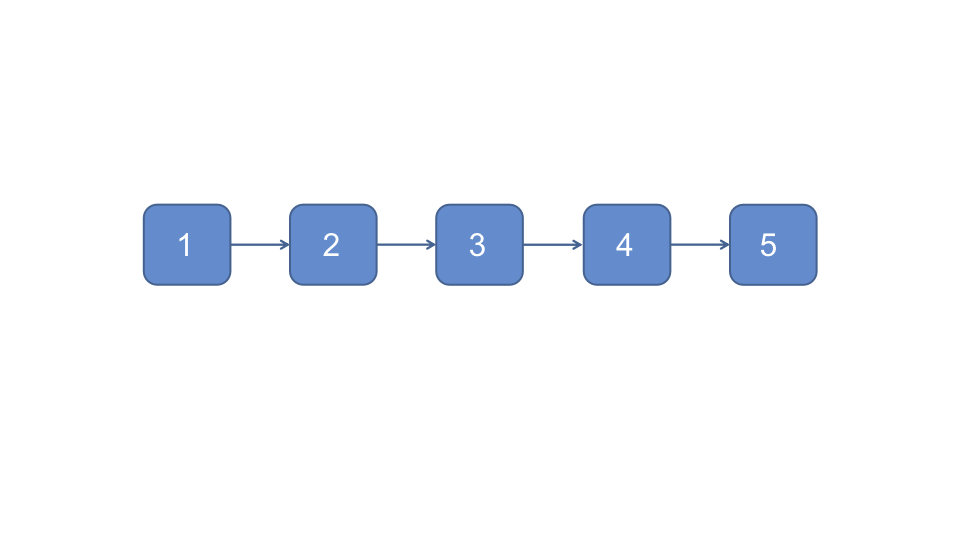
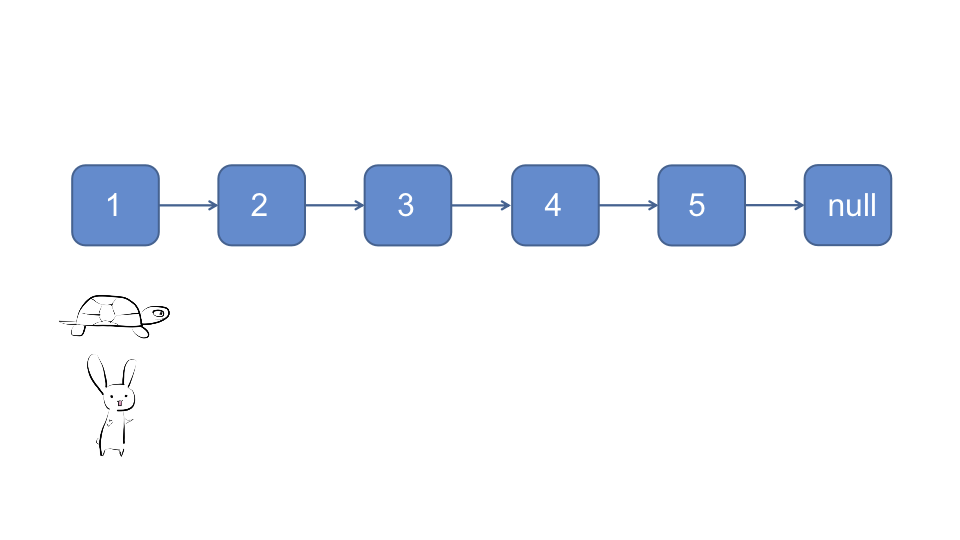
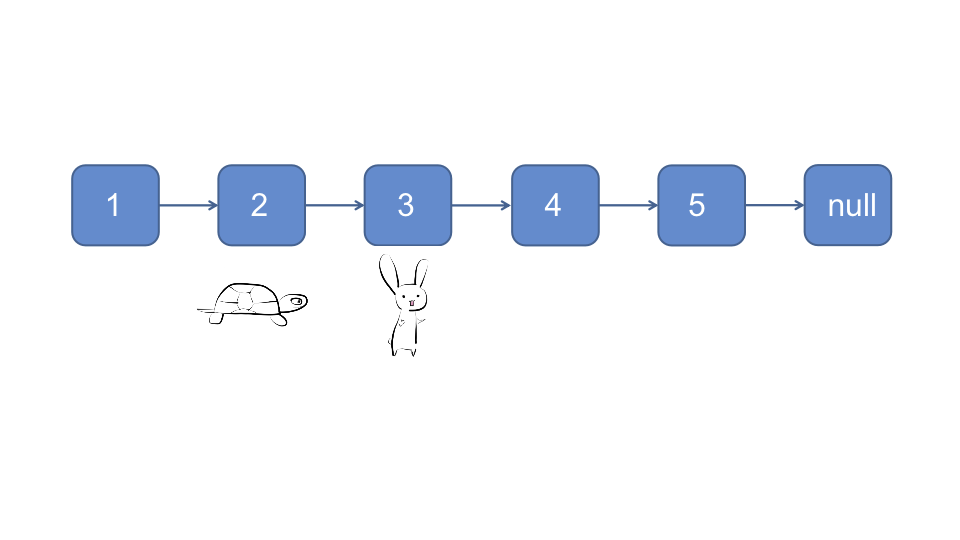
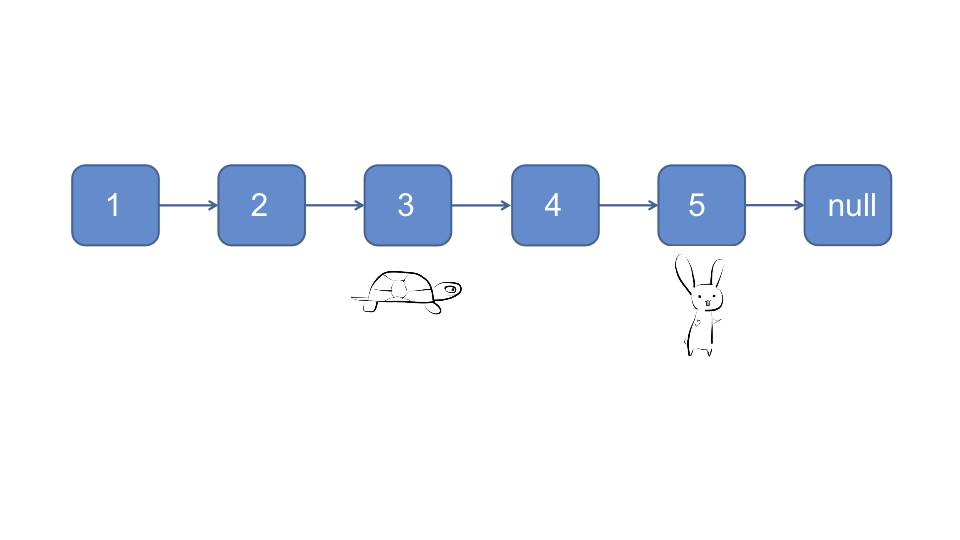
对于偶数链表, 当快指针指向null时, 慢指针指向的节点即为所求

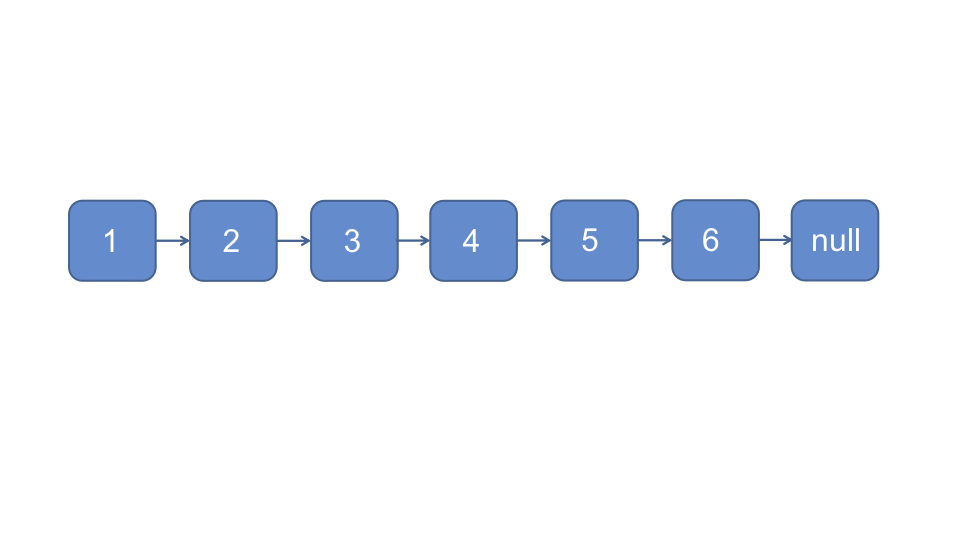
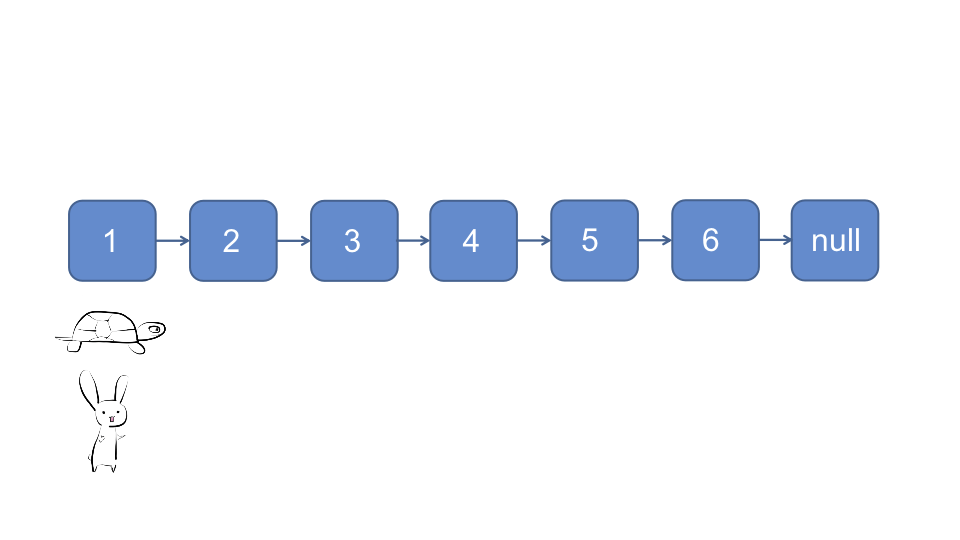
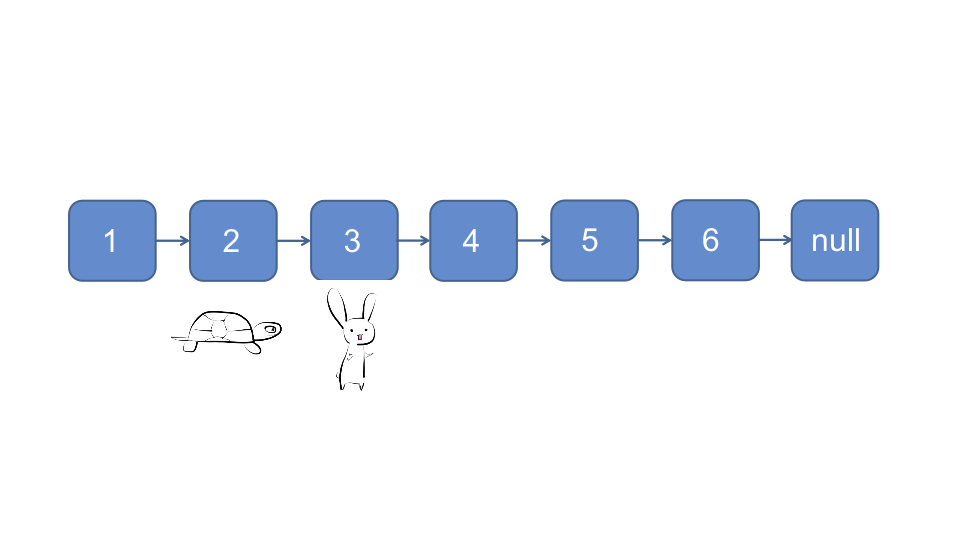
var middleNode = function(head) {
  let slowPointer = head
  let fastPointer = head
  while (fastPointer !== null && fastPointer.next !== null) {
    slowPointer = slowPointer.next
    fastPointer = fastPointer.next.next
  }
  return slowPointer
};

回文链表

把链表变成双向链表, 并从两端向中间比较

时间复杂度为O(n), 因为要存储prev指针, 所以空间复杂度为O(n)

var isPalindrome = function(head) {
  if (head === null) {
    return true
  } else {
    let headPointer = head
    let tailPointer = head
    while (tailPointer.next) {
      tailPointer.next.prev = tailPointer
      tailPointer = tailPointer.next
    }
    while(headPointer !== tailPointer) {
      if (headPointer.next !== tailPointer) {
        if (headPointer.val === tailPointer.val) {
          headPointer = headPointer.next
          tailPointer = tailPointer.prev
        } else {
          return false
        }
      // 考虑偶数链表
      } else {
        return headPointer.val === tailPointer.val
      }
    }
    return true
  }
};

快慢指针

慢指针🐢依次访问下一个节点, 并翻转链表
快指针🐰依次访问下下一个节点, 直到快指针🐰没有下一个节点(奇数链表)或者快指针指向null(偶数链表), 此时已完成了前半截链表的翻转
依次比较前半截链表和后半截链表节点的值

对于奇数链表:

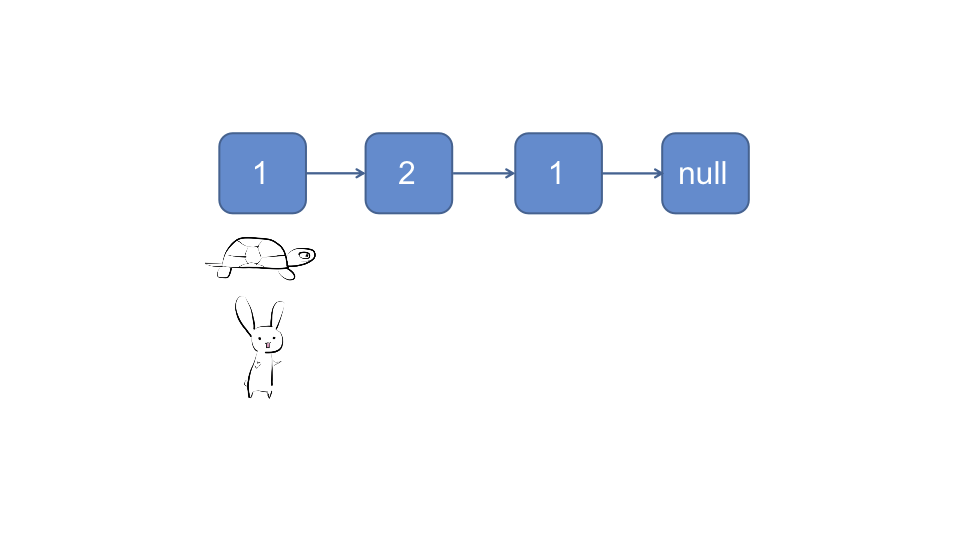
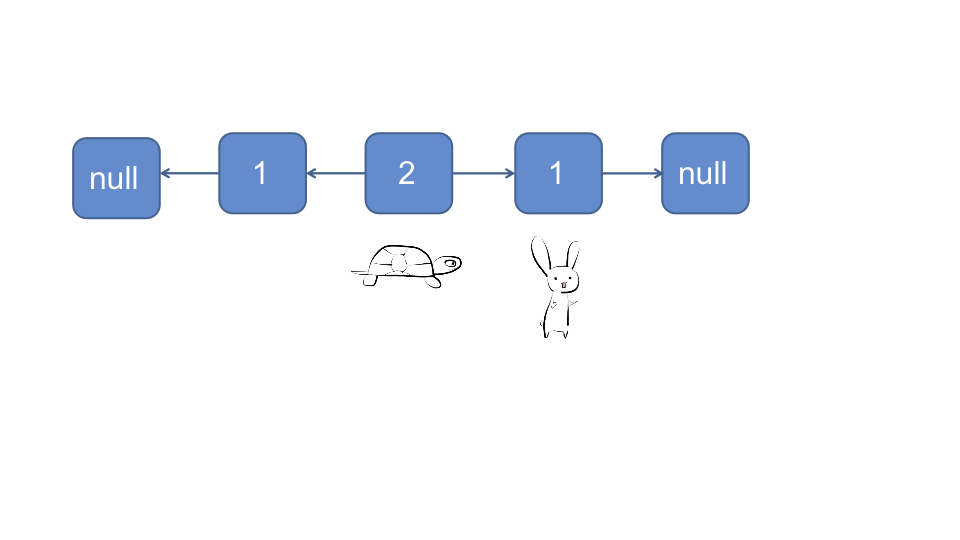
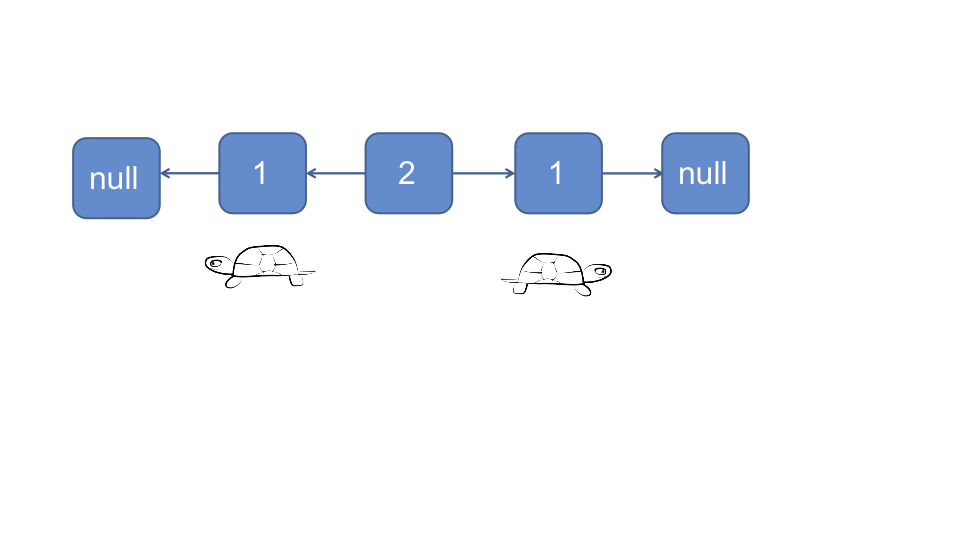
对于偶数链表:

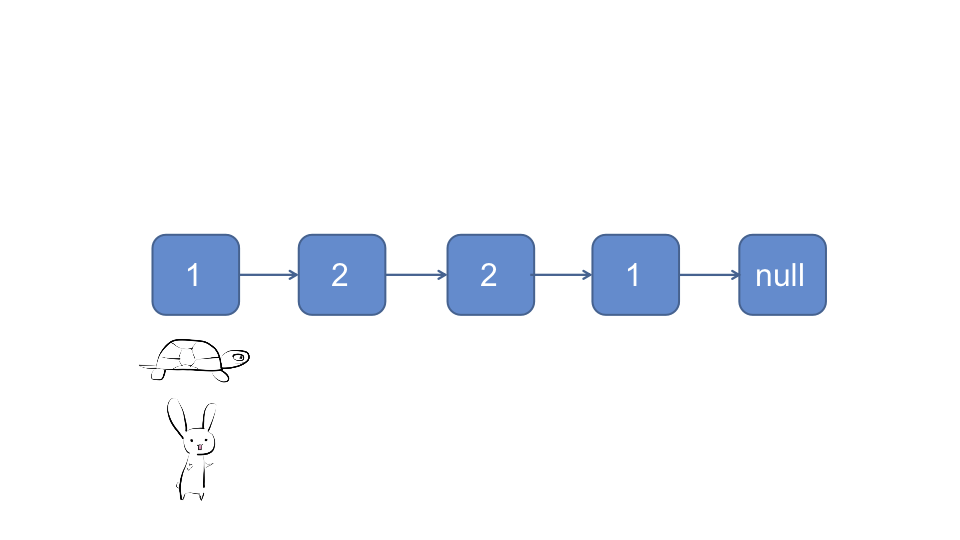
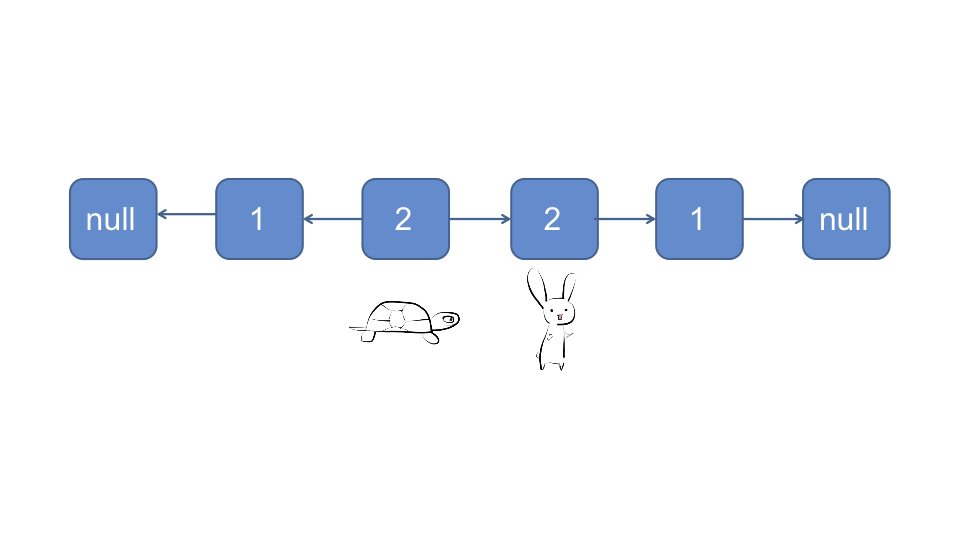
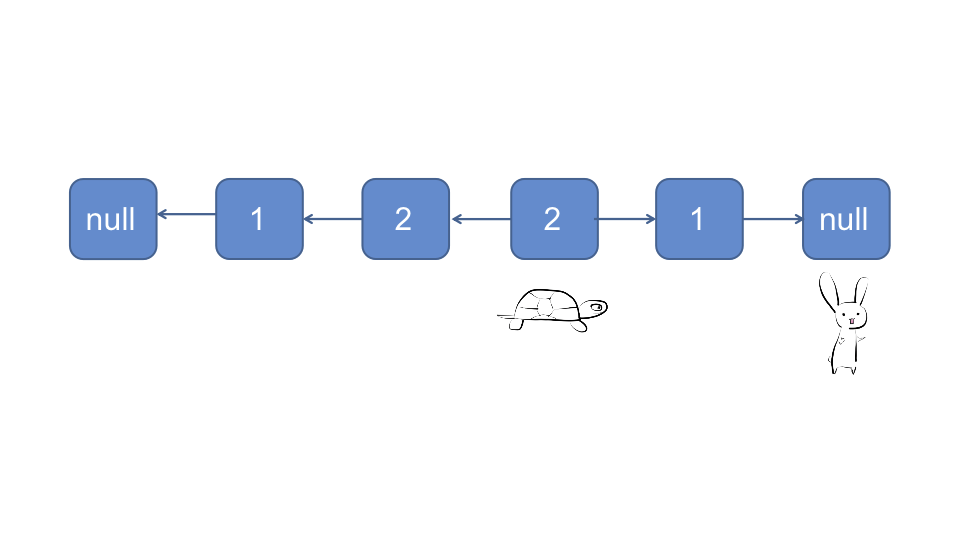
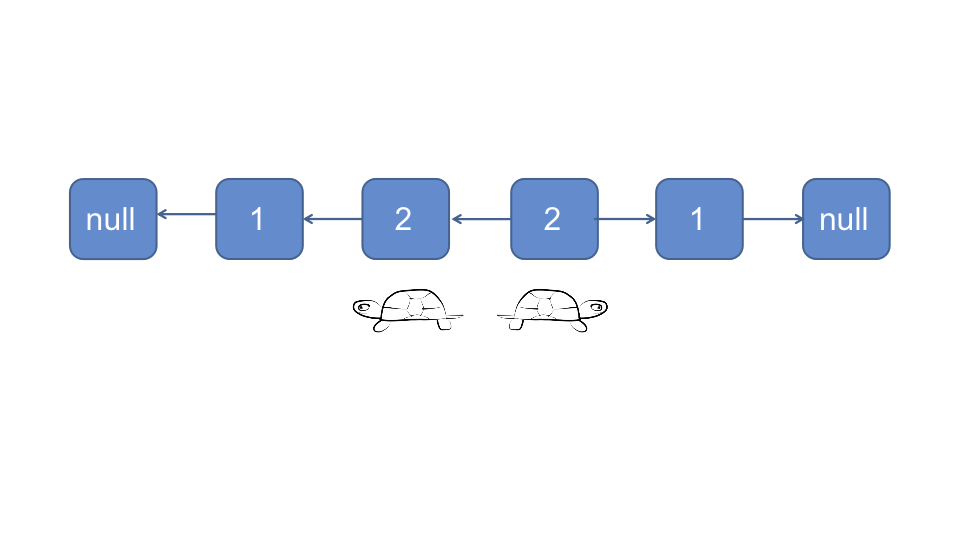
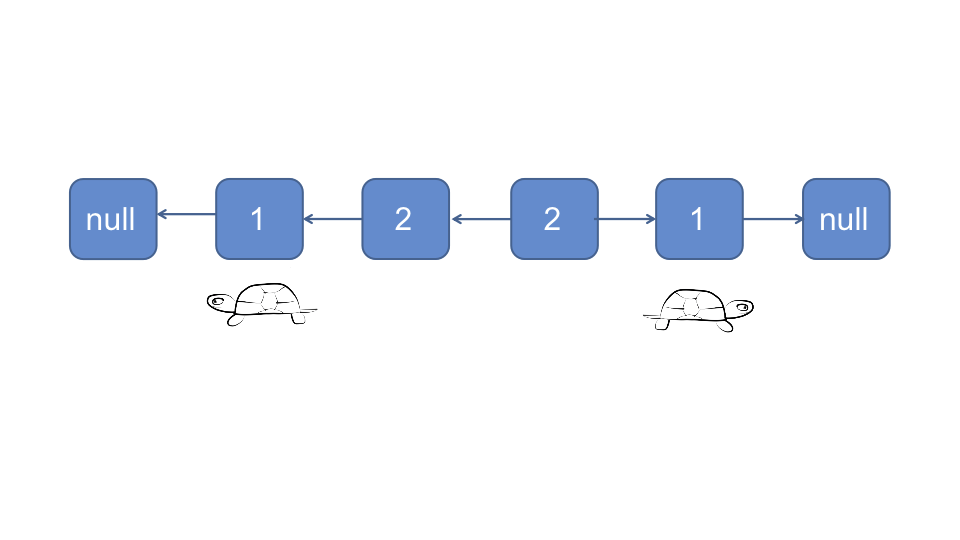
时间复杂度O(n), 空间复杂度O(1)

var isPalindrome = function(head) {
  if (head === null) {
    return true
  } else if (head.next === null) {
    return true
  } else {
    let slowPointer = head
    let fastPointer = head
    let _head = null
    let temp = null
    // 找到中间节点, 并翻转前半截链表,
    // 让_head指向翻转后的前半截链表的头部,
    // 让slow指向后半截链表的头节点
    while (fastPointer && fastPointer.next) {
      _head = slowPointer
      slowPointer = slowPointer.next
      fastPointer = fastPointer.next.next
      _head.next = temp
      temp = _head
    }
    // 奇数链表跳过最中间的节点
    if (fastPointer) {
      slowPointer = slowPointer.next
    }
    while (_head) {
      if (_head.val !== slowPointer.val) {
        return false
      }
      _head = _head.next
      slowPointer = slowPointer.next
    }
    return true
  }
};

快乐数

循环并缓存每次获取位的平方和, 如果已缓存过, 就退出循环, 判断退出循环后是否为1, 缺点: 需开辟O(n)的存储空间

var isHappy = function(n) {
  const memory = {}
  while (n !== 1) {
    function getBitSquareSum (n) {
      let sum = 0
      while (n !== 0) {
        const bit = n % 10
        sum += bit * bit
        n = parseInt(n / 10)
      }
      return sum
    }
    n = getBitSquareSum(n)
    if (memory[n] === undefined) {
      memory[n] = 1
    } else {
      break
    }
  }
  return n === 1
};

慢指针🐢获取一次每位的平方和, 快指针🐰获取两次每位的平方和, 当两个指针值一样时判断其是否为1

对于19这个数, 快慢指针会在每位的平方和为1时相遇, 兔子会在1处等乌龟

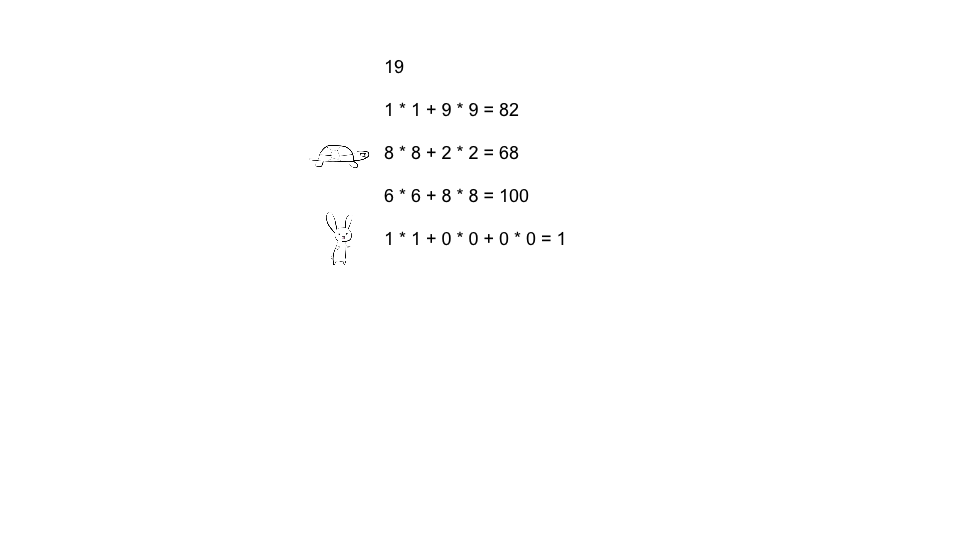
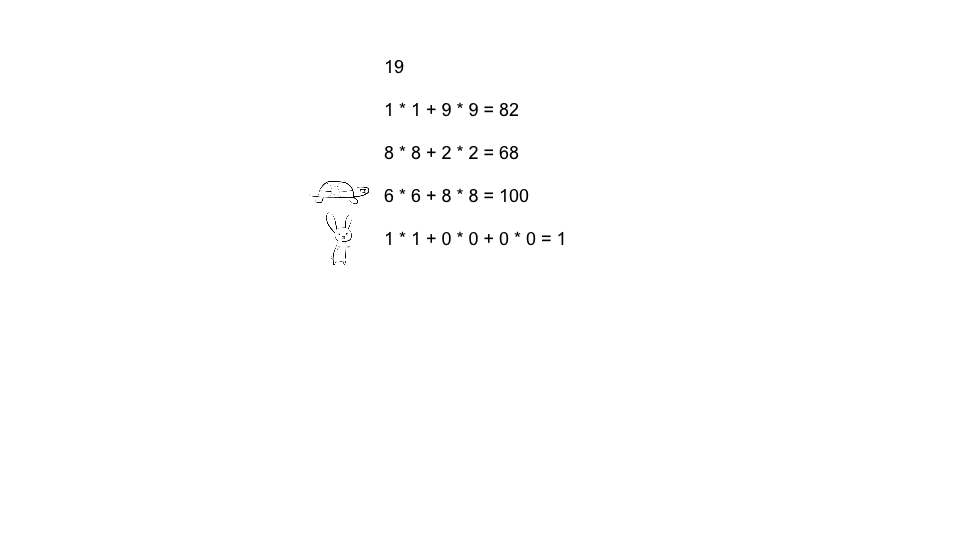
对于37这个数, 对其反复的求每位的平方和会进入循环, 而且进入循环时其值不为1

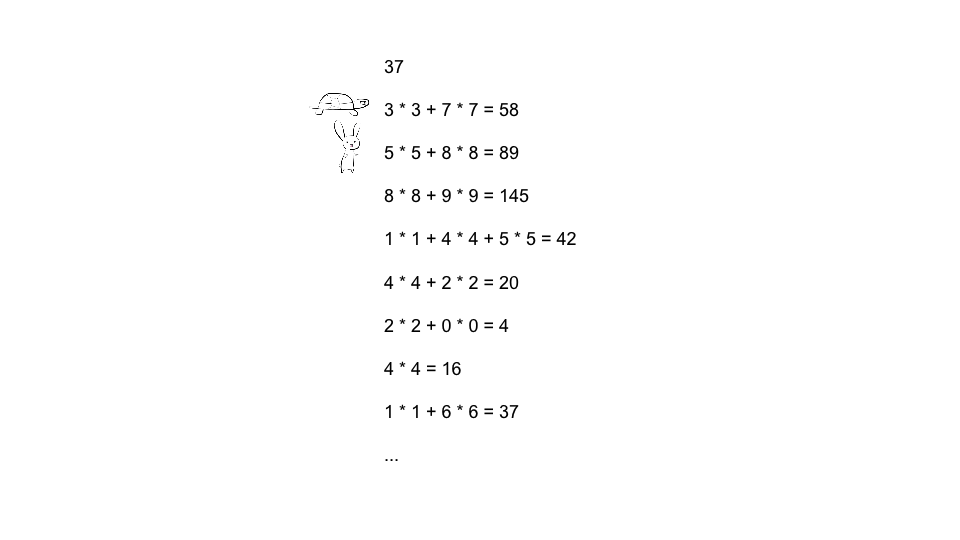
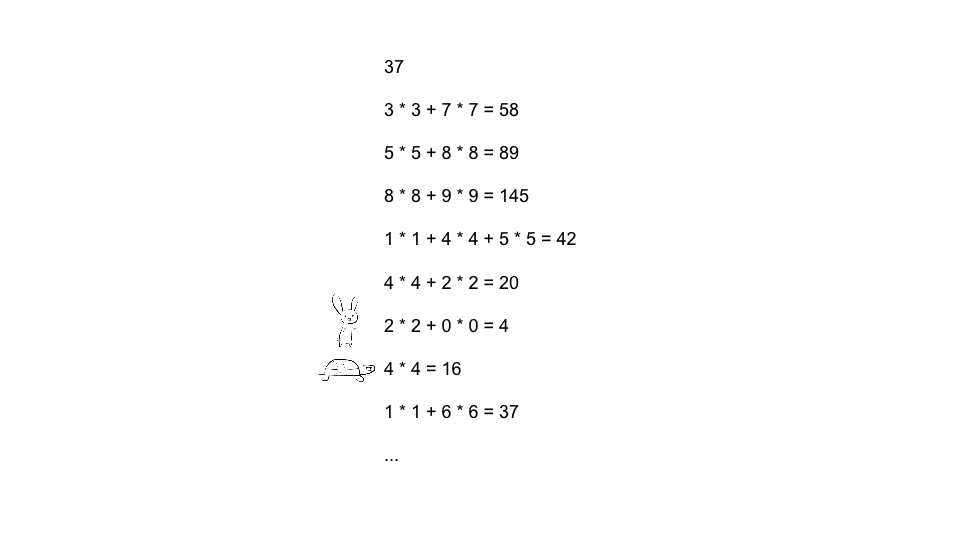
var isHappy = function (n) {
  let slowPointer = n
  let fastPointer = n
  function getBitSquareSum (n) {
    let sum = 0
    while (n !== 0) {
      const bit = n % 10
      sum += bit * bit
      n = parseInt(n / 10)
    }
    return sum
  }
  do {
    slowPointer = getBitSquareSum(slowPointer)
    fastPointer = getBitSquareSum(getBitSquareSum(fastPointer))
  } while (slowPointer !== fastPointer)
  return slowPointer === 1
}

总结

在一些场景, 如链表数据结构和判断循环, 利用快慢指针创造的差值, 可节省内存空间, 减少计算次数

快慢指针, 一对快乐的指针, just be happy!

原文在掘金: juejin.cn/post/684490…

[leetcode]灵魂画师图解🎨快慢指针在算法中的应用