为什么使用卡尔曼滤波器?
卡尔曼滤波器是一种优化估算算法,在不确定和间接测量的情况下估算系统状态。

- 可以对感兴趣的变量进行直接测量
- 可以综合各个可能含有噪声的传感器来进行准确的估计测量
状态观测器

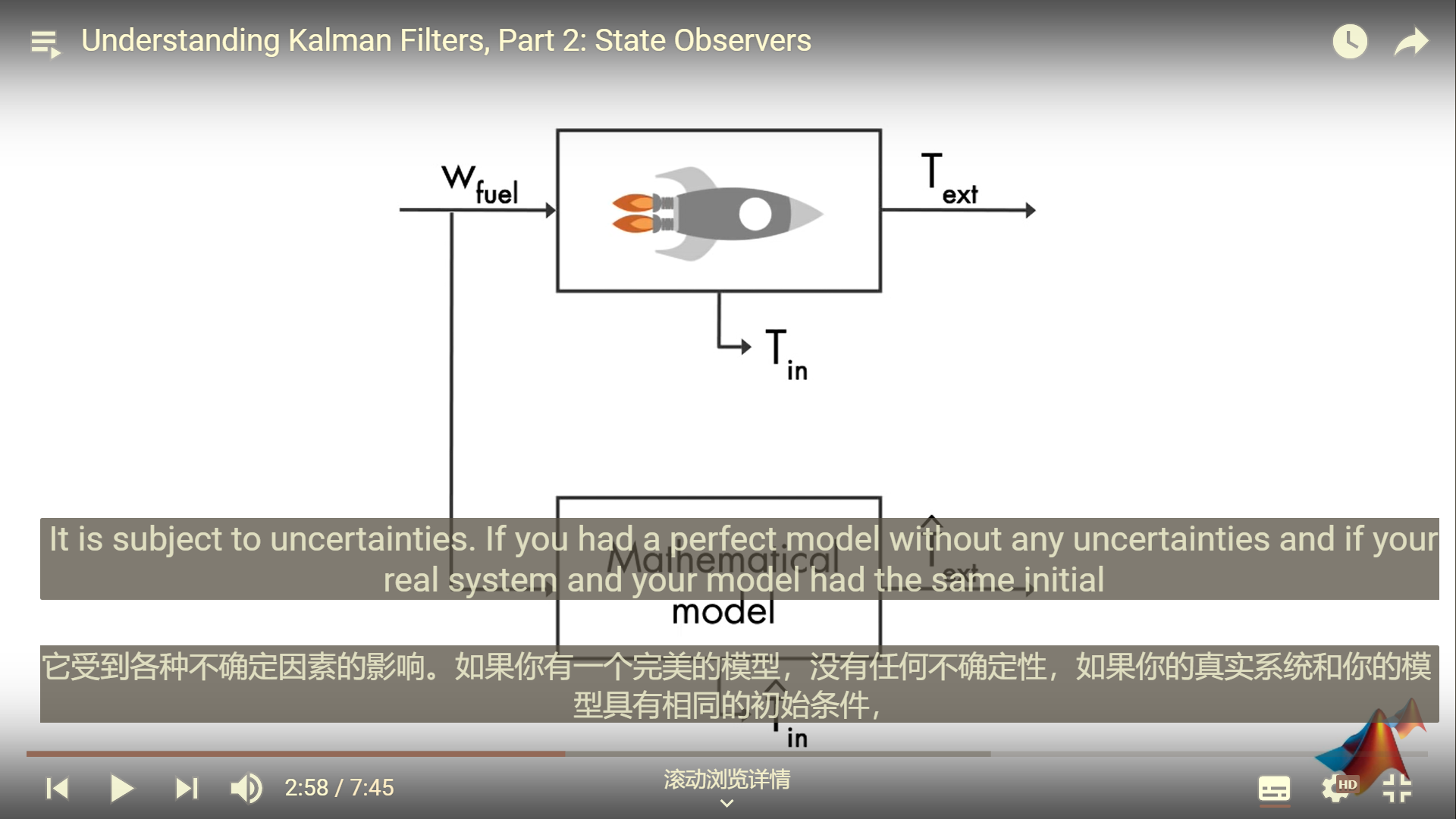
完美模型(微分方程/差分方程)+相同的初始条件 那么这个观测器就百分百准确,但是不可能做到
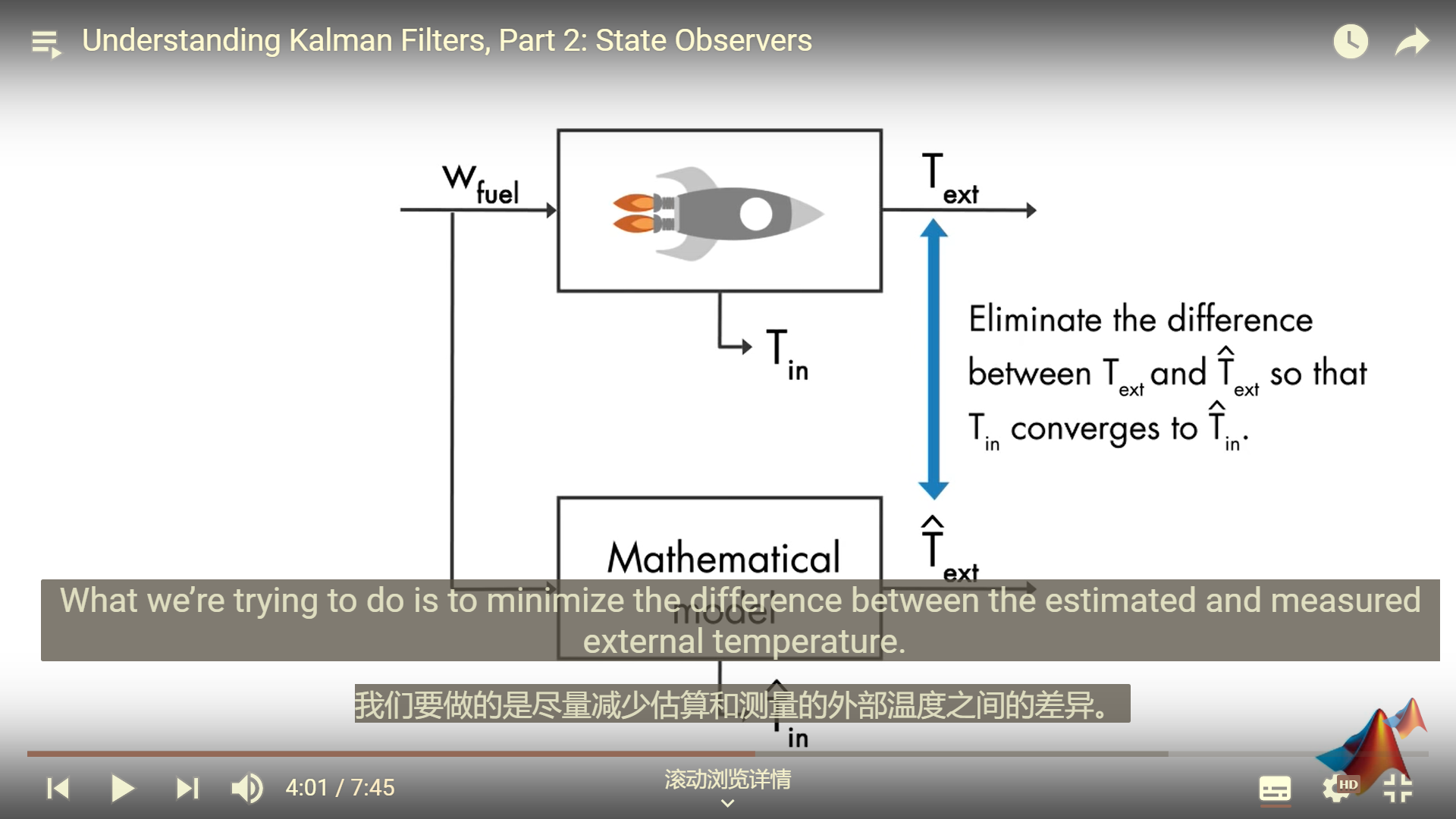
只要两个可测量量相等,那么 Tin也就相同
引入闭环反馈系统,引入增益K,减小两个可测量量的误差
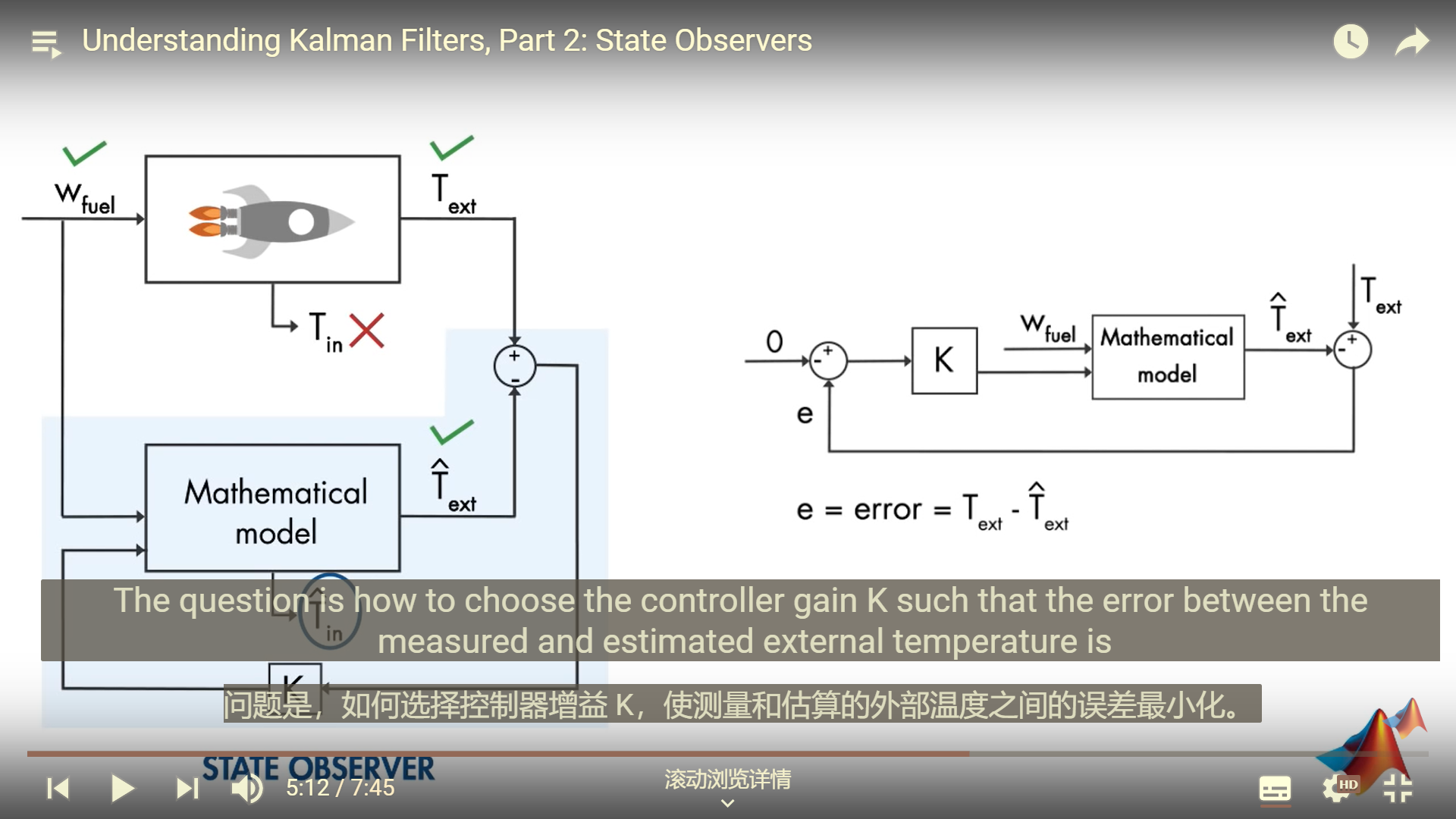
输入燃料,运行观测器得到,同时并且得到可测量量
,综合这两个值的error,然后选择控制器增益K,和输入一起扔进model里面估计出系统的内部状态

K用kalman filter 来确定
最优状态估计
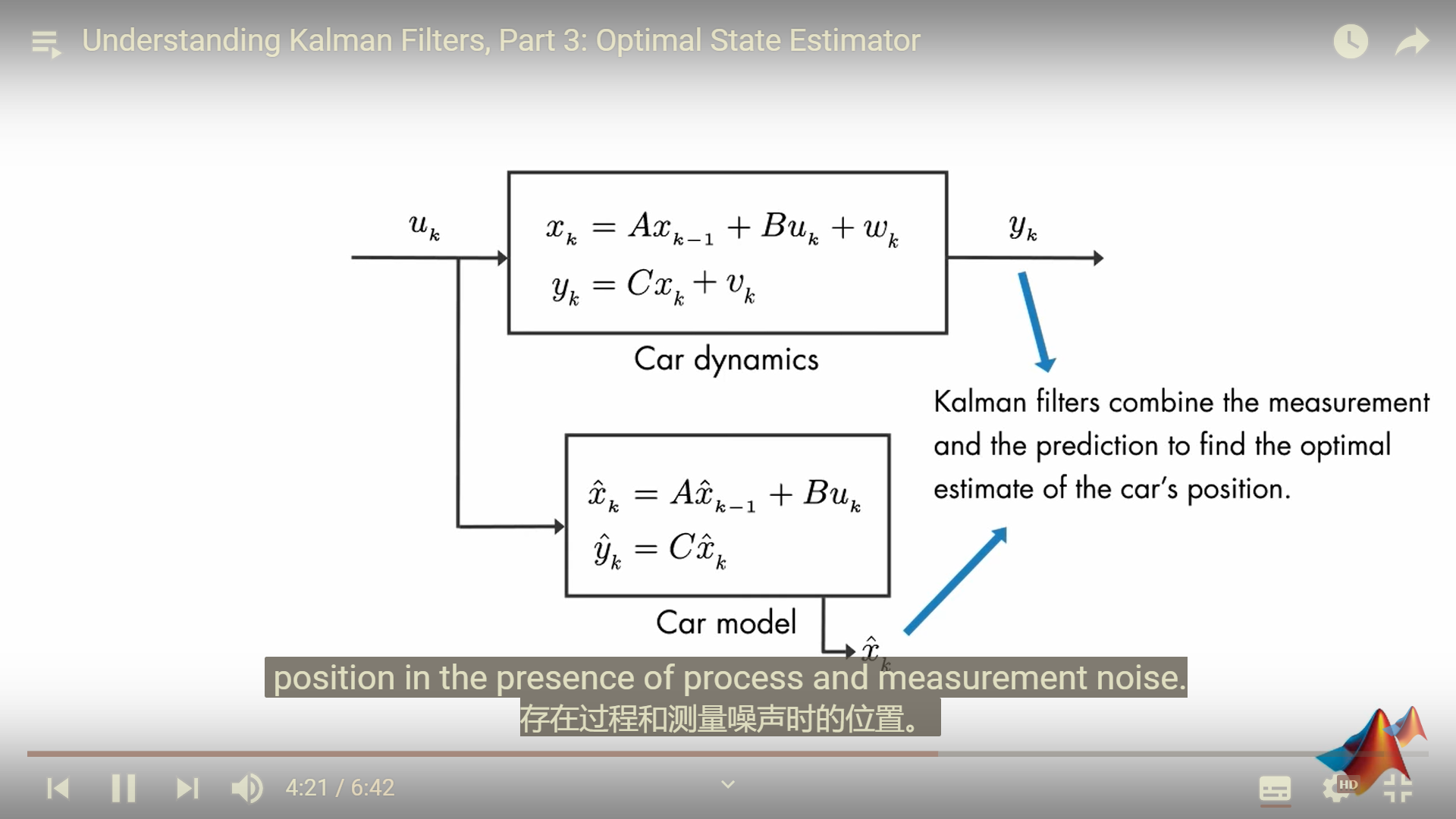
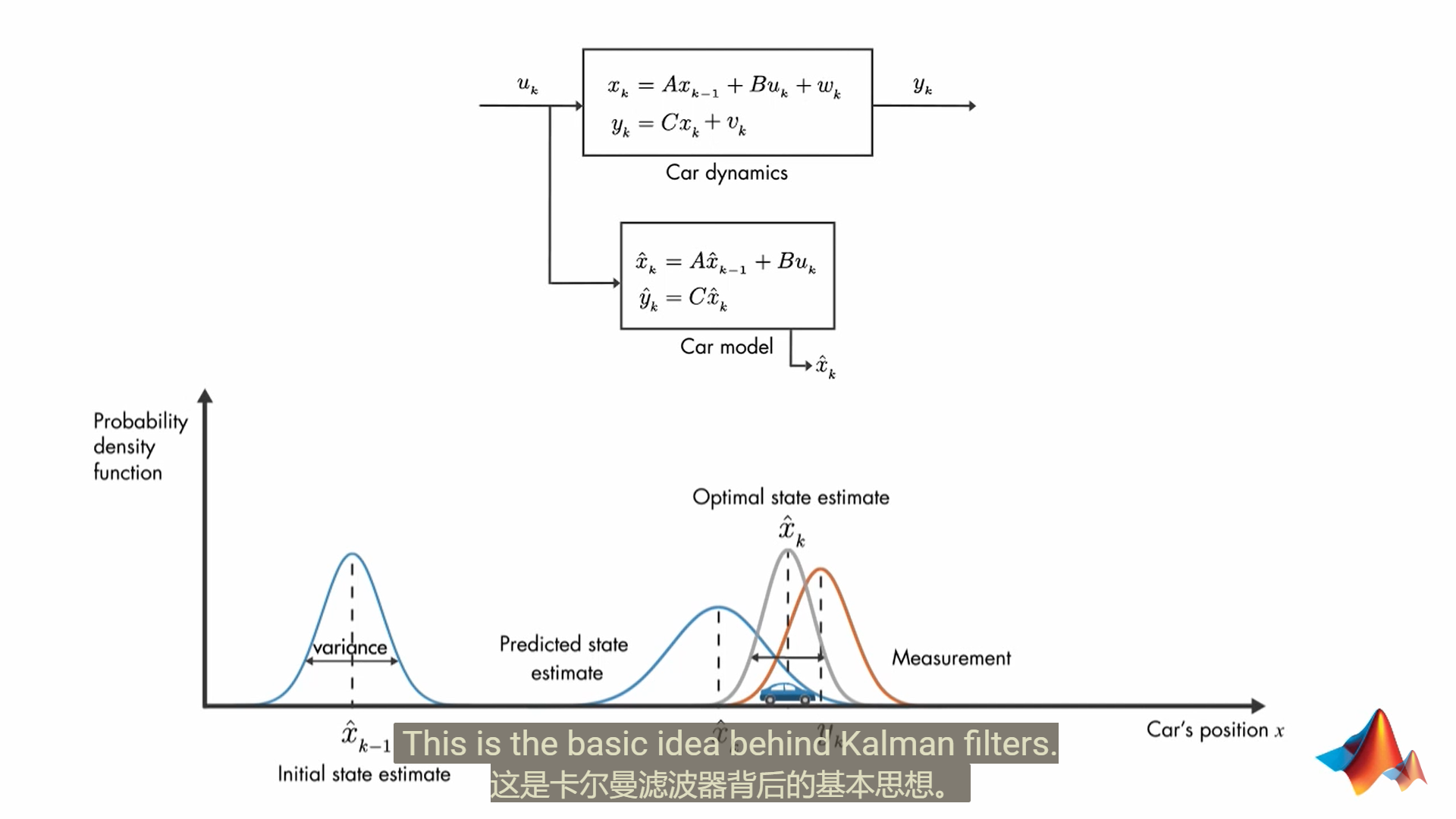
预测状态估计的概率密度和测量值的概率密度乘积,得到最优状态估计的概率密度,其mean就是我们的最有估计值
最优状态估计算法和方程
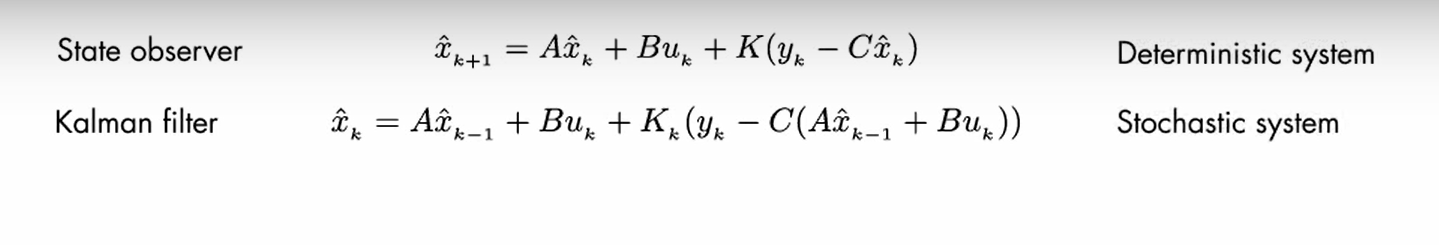
卡尔曼滤波器就是一种状态观测器,但它是为随机系统设计的

kalman filter分成两部分
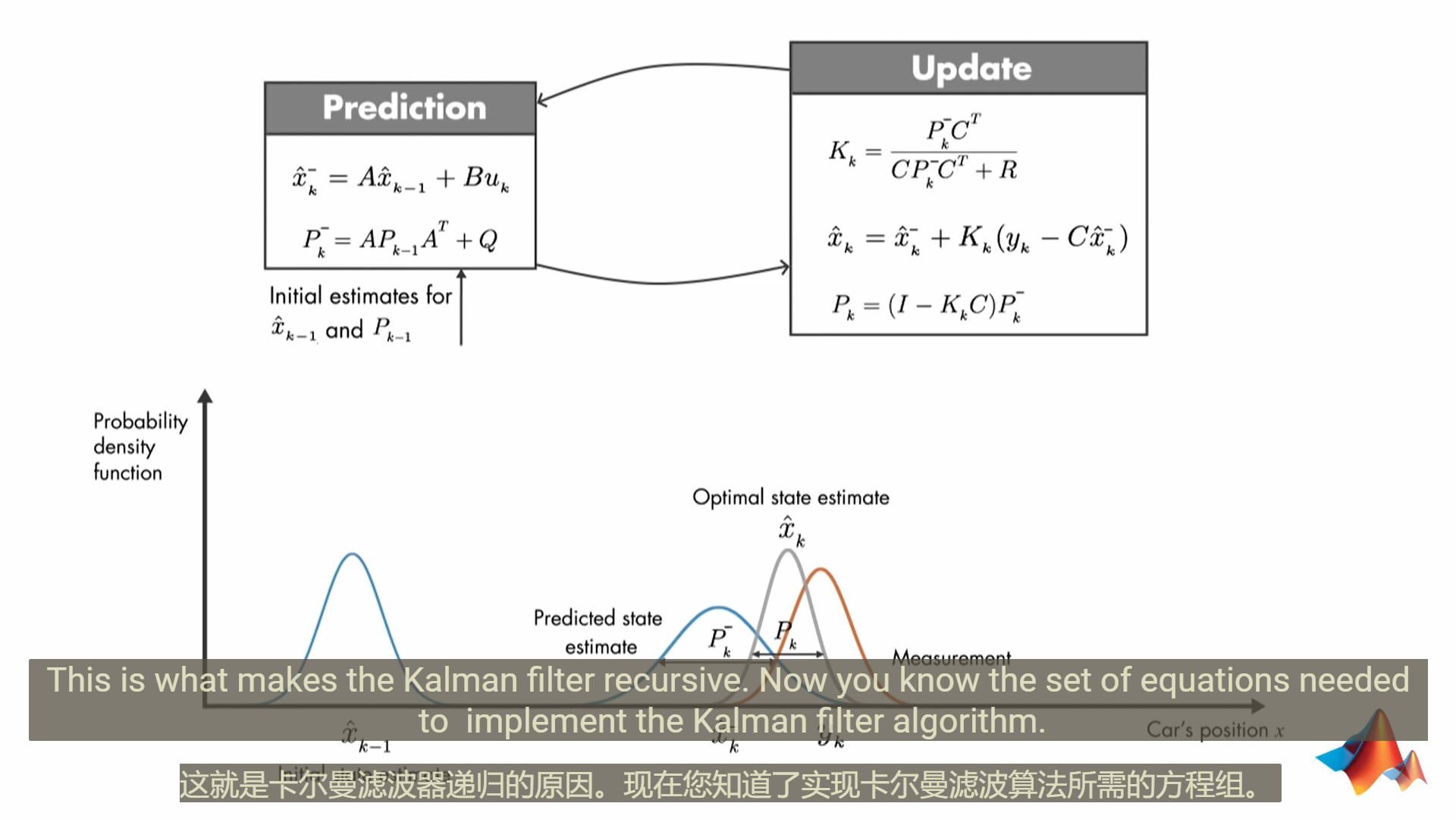
不断迭代,不断更新,最终 就会收敛到最优估计状态值
以下为有两个传感器的情形(有两个测量值)
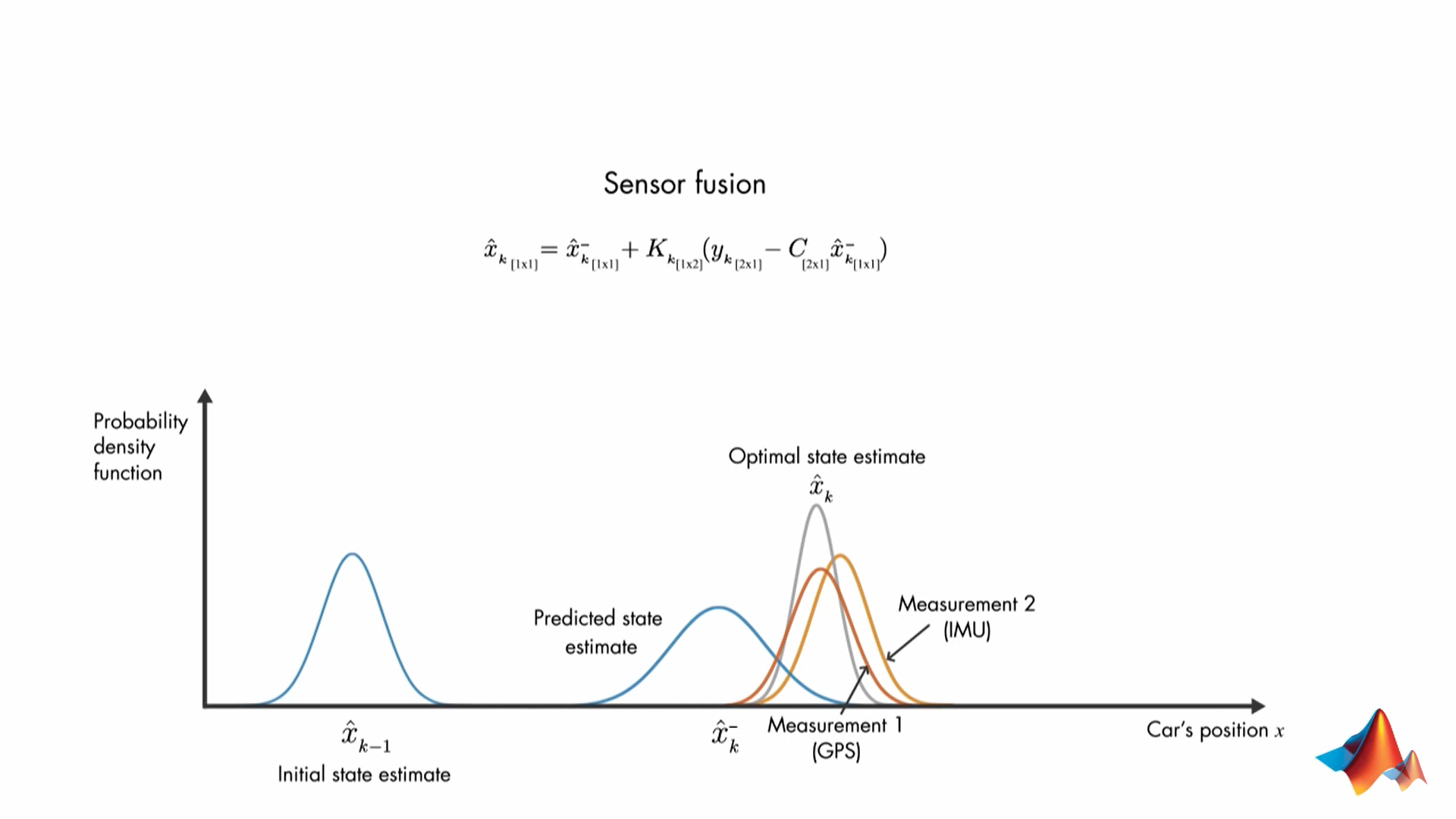
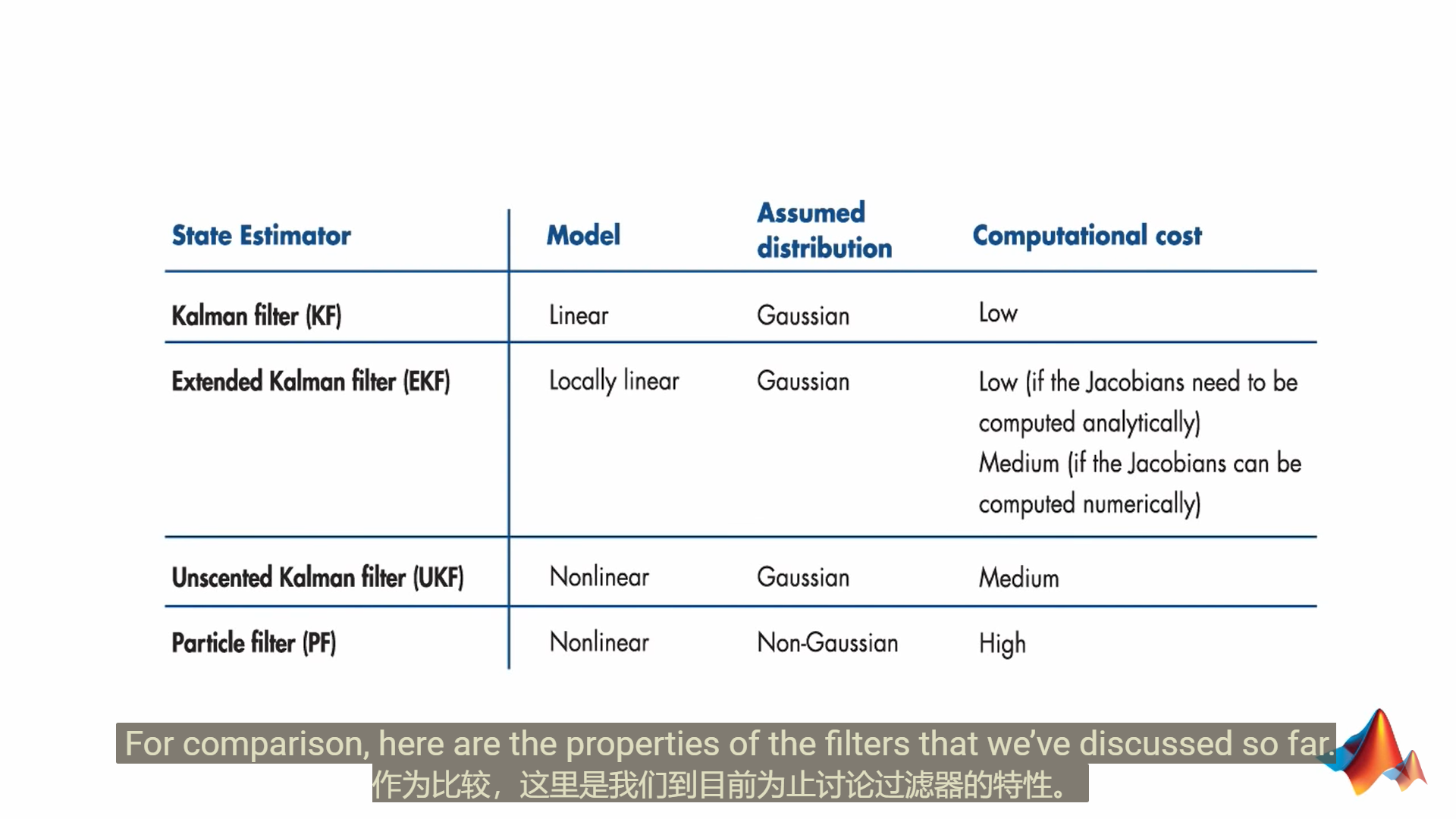
非线性状态估计器


卡尔曼滤波器仅针对线性系统
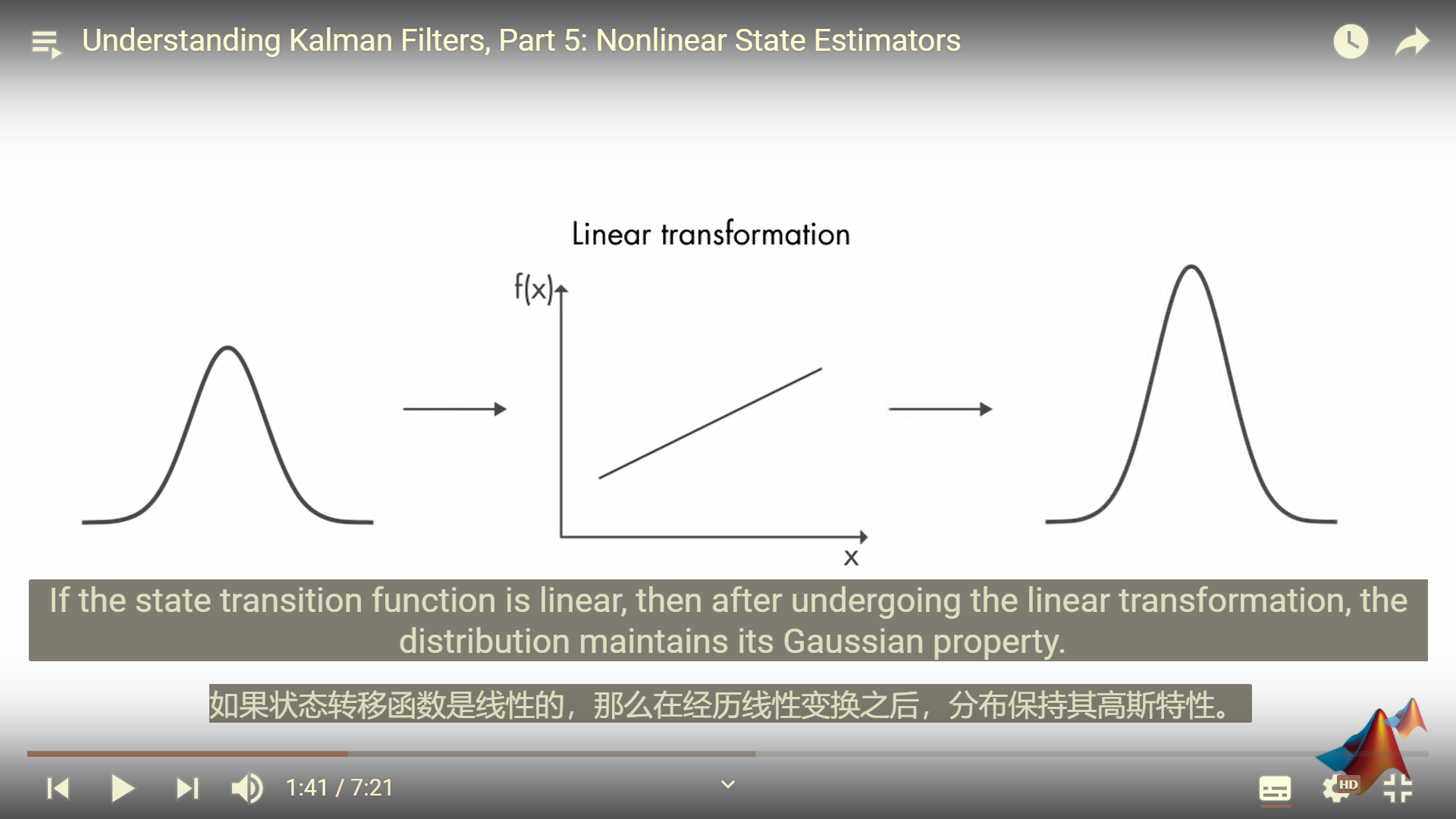
观测函数 g(x) 也是如此
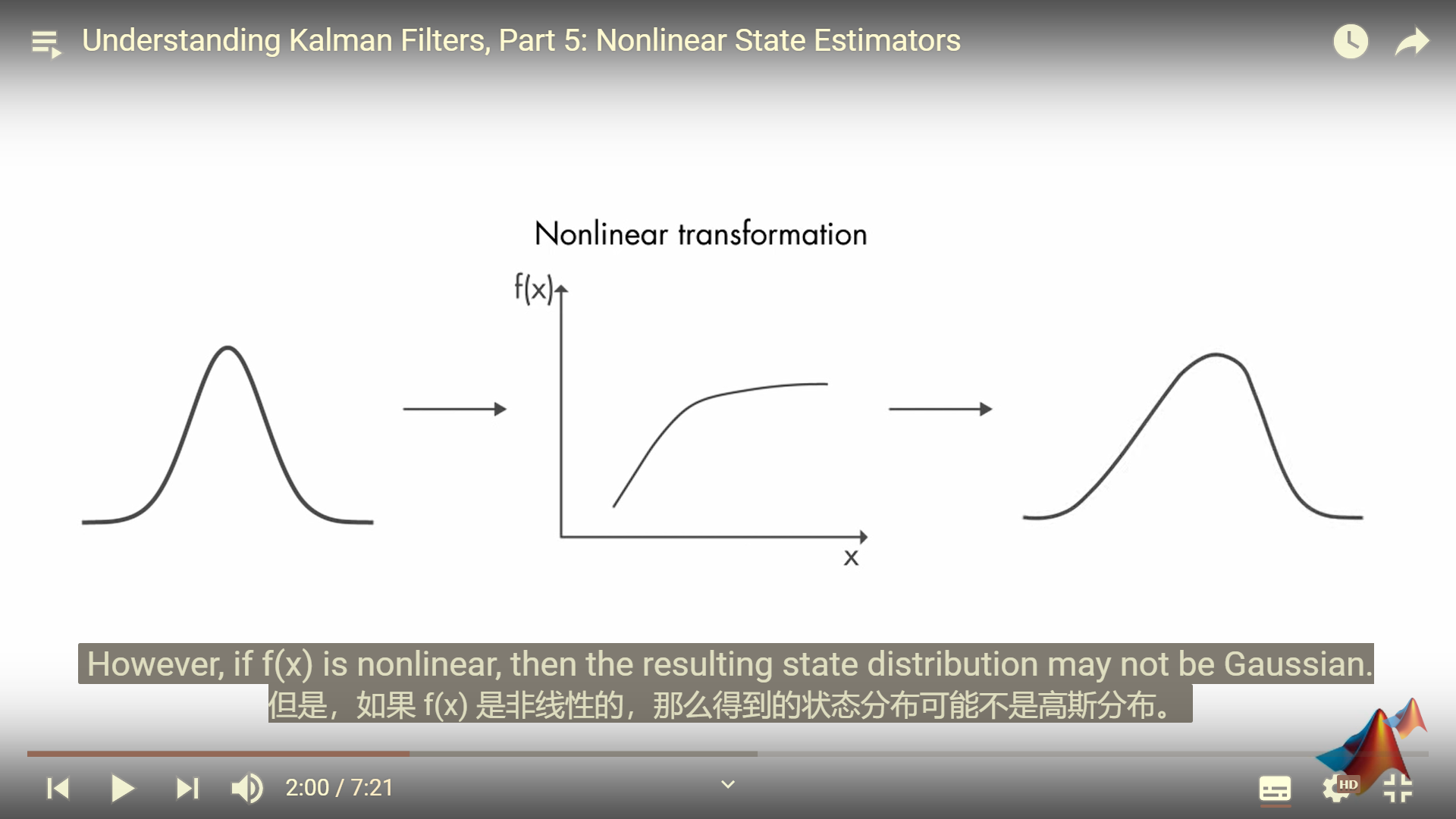
因此,卡尔曼滤波器算法可能会不收敛。
扩展卡尔曼滤波器(EKF)
它把非线性函数在当前估算状态的平均值附近进行线性化。在每个时间步,执行线性化,然后将得到的雅可比矩阵用于预测和更新卡尔曼滤波器算法的状态。

然而,它有以下缺点:
- 由于复杂的导数,可能难以解析计算雅可比矩阵;
- 而以数值方式计算它们则可能需要很高的计算成本;
- 扩展卡尔曼滤波器不适用于具有不连续模型的系统,因为系统不可微分时雅各比矩阵不存在;
- 高度非线性系统的线性化效果不好。
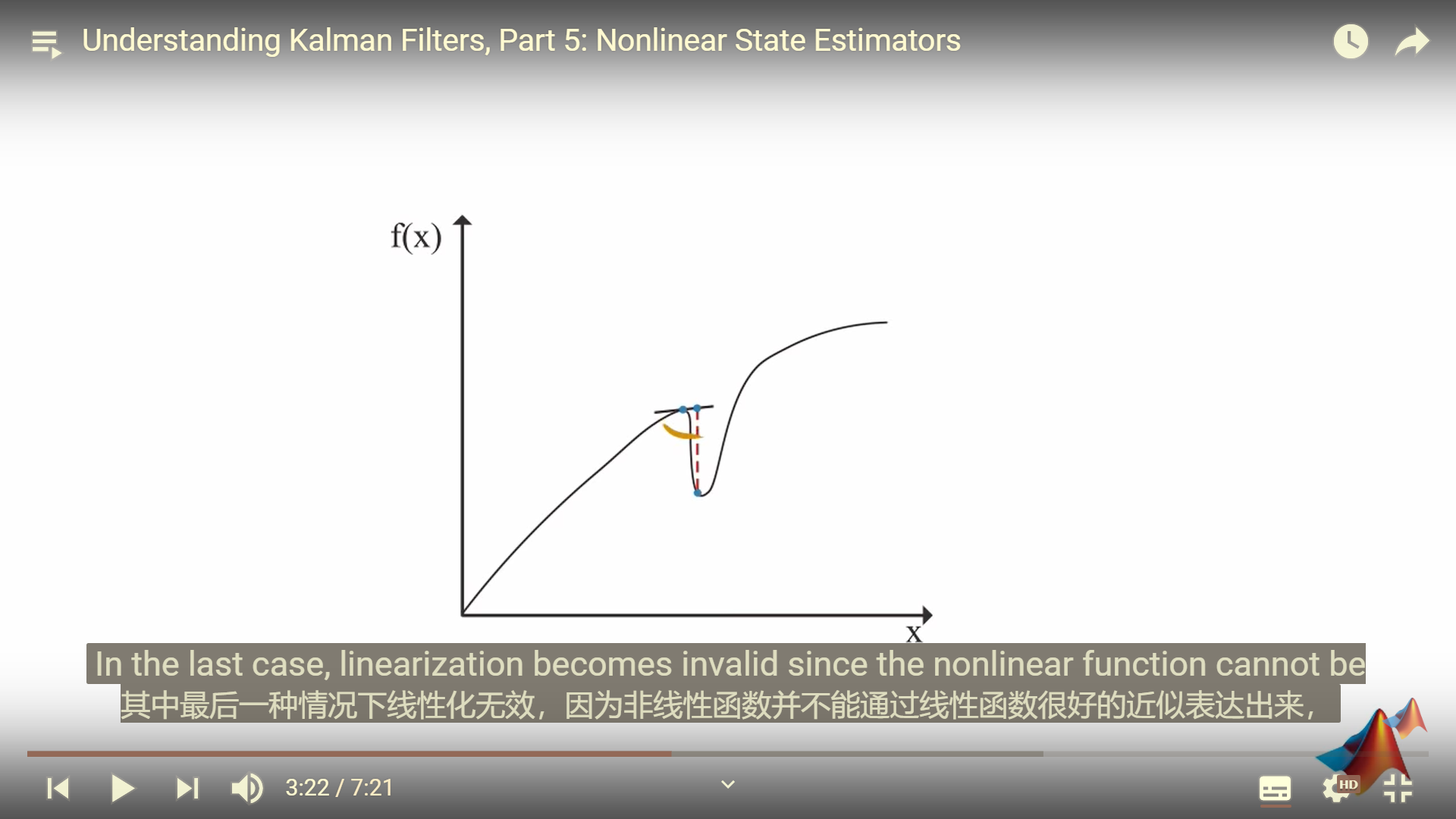
无迹卡尔曼滤波器unscented Kalman filter (UKF)
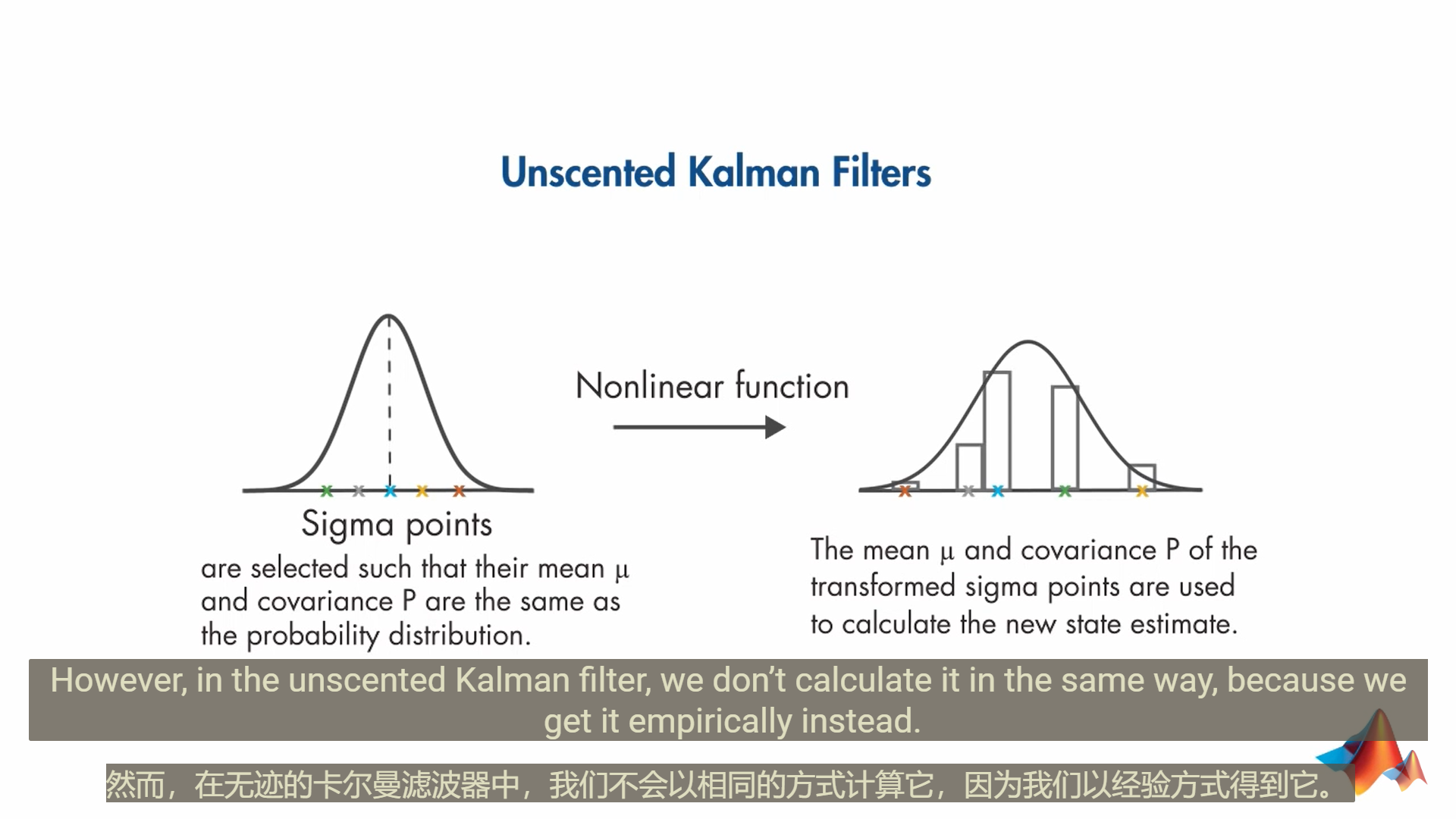
粒子滤波器(PF)
与无迹卡尔曼滤波器的显着差异在于,粒子滤波器近似任意分布,所以它不仅限于高斯假设