前言

任意优先队列都可以变成一种排序方法。假设对于一个删除最大元素的优先队列，不断地调用删除最大元素，置于某队列中，如此当优先队列中原先的全部元素遍历完后，我们就可以得到一个有序数组。代码也会放于CodePen之上（在后文）。

本文使用之前所学习的掘金——基于二叉堆的优先队列实现堆排序，也将基于前文的方法名。

堆排序可以分为两个阶段：

• 堆构造阶段：将原数组重新组织安排进一个堆中
• 下沉排序阶段：从堆中按递减顺序取出元素得到排序结果

后文将直接使用需要排序的数组作为堆，通过记录下标控制不断变化的堆的大小，这样就不需要额外的空间

堆构造阶段

给定N个元素的数组，用此数组来构造堆。

最简单直接的方法就是用swim()方法从左向右遍历元素。但是有一个更加高效的方法：即使用sink()从中间向右构造堆。

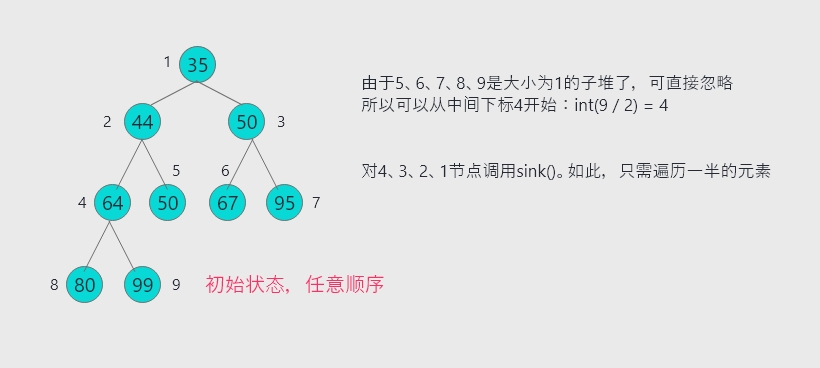
堆构造阶段完成后这个数组就已经是堆有序了

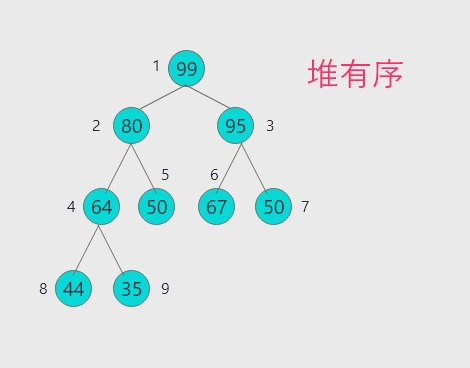
接下来进行下沉排序

下沉排序阶段

堆排序的排序流程主要是在下沉排序阶段完成的，思路也非常简单：删除堆中最大元素，放入堆缩小后空出来的数组位置

如此每次取出来的元素都是按顺序排列，直至所有元素取完，便是一个从小到大的有序数组。（这个过程和选择排序有些类型）

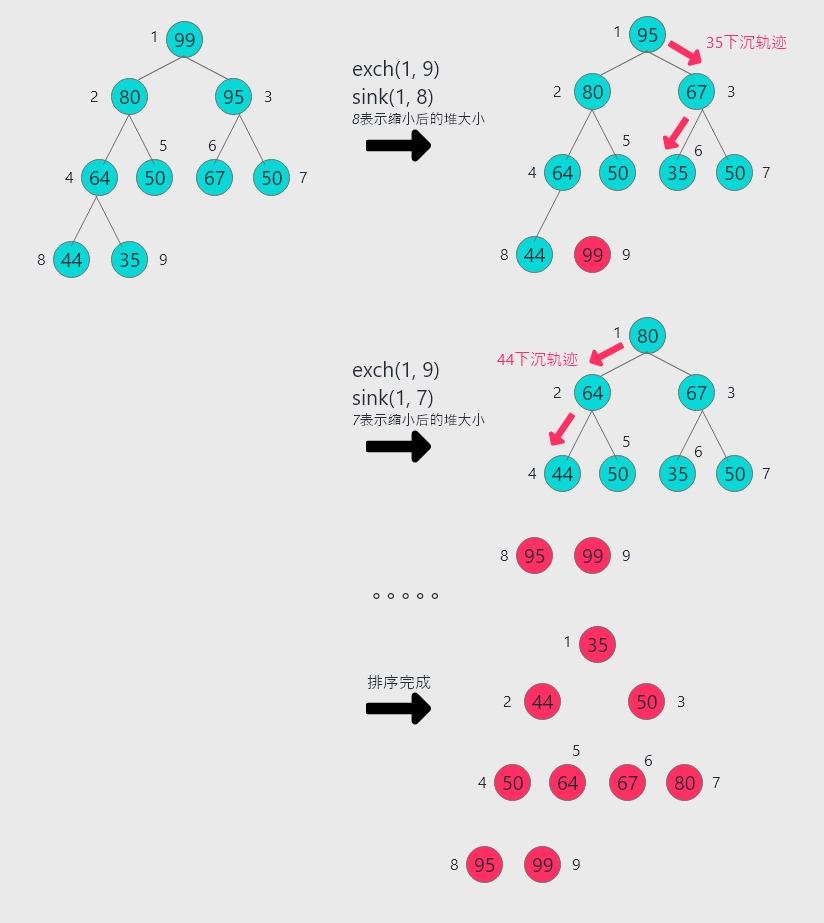
代码

在理解整个流程后，代码其实非常简单，堆构造阶段是用sink()对原数组的遍历，下沉排序阶段是用exch()交换元素，缩小堆，用sink()下沉新的根节点

  sort() {
    let lastIndex = this.volume;
    //第一阶段：构造堆阶段
    for (let k = Math.floor(lastIndex / 2); k >= 1; k--) {
      this.sink(k, lastIndex);//sink()函数在上一篇文章的基础上有所更改
    }

    //第二阶段：下沉排序阶段
    while (lastIndex > 1) {
      this.exch(1, lastIndex);
      lastIndex--;
      this.sink(1, lastIndex)
    }
  }

CodePen打开

总结

在了解基于二叉堆的优先队列后实现此排序确实不难，也令人感觉优先队列的强大之处。

在实际应用中，优先队列还可用于粒子碰撞模拟、数据压缩等等

参考资料

《算法（第4版）》