前言

对于应用程序而言，经常需要有序的元素，但是有时他们并不要求完全有序，而仅仅要求其中最大或最小的一个元素。同时，数组也可能随时添加新的元素，接着再取其中最大或最小的元素。

举个例子，操作系统中对事件的处理，每次都会处理优先级最高的事件，同时新的事件又可能不断地推入。

当然你可以说每次推入时重新进行排序，但是这样是否会效率太低呢？是否有更高效的方法？

抽象出来，我们需要的数据结构应该满足如下两个操作：删除（取出）最大元素和插入元素。这种数据类型便是优先队列。

优先队列是一种抽象数据类型，本文我们将实现一个基于二叉堆的优先队列。

以下是代码先放：CodePen打开

二叉堆定义

二叉堆（英语：binary heap）是一种特殊的堆，二叉堆是完全二叉树或者是近似完全二叉树。二叉堆满足堆特性：父节点的键值总是保持固定的序关系于任何一个子节点的键值，且每个节点的左子树和右子树都是一个二叉堆。
当父节点的键值总是大于或等于任何一个子节点的键值时为“最大堆”。当父节点的键值总是小于或等于任何一个子节点的键值时为“最小堆”。——摘自维基百科——二叉堆

看图例

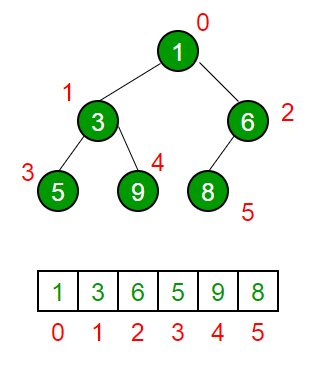
有同学可能会有疑问，那堆和树又有什么关系，在知乎上看到一张很好的图

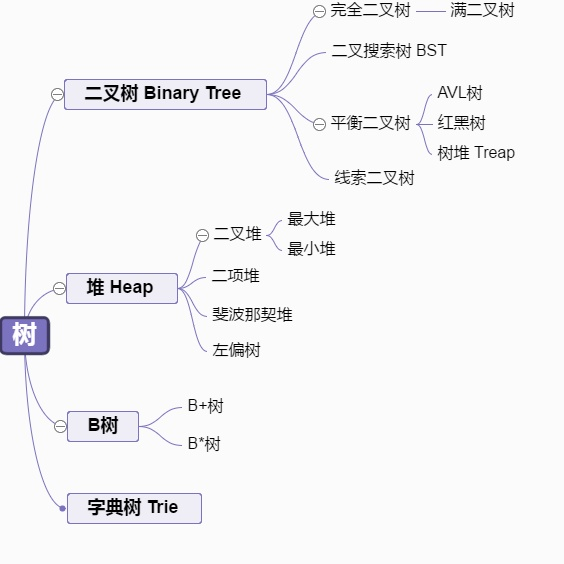
对一棵二叉树来说，二叉树的每个节点大于等于（或小于等于）它的子节点时，它被称为堆有序。

简单说，二叉堆是一组堆有序的二叉树，并在数组中按照层级存储。

二叉堆有如下特性可以帮助我们实现优先队列：

数组无需指针，可直接通过下标访问
k节点的父节点为下标int( k/2 )，两个子节点下标为2*k，2*k+1（**注意：**数组0位置不放元素，从1位置开始放）
一颗大小为N的二叉树高度为lgN（向下取整）

此文中我用最大堆作为例子

二叉堆的算法

了解二叉堆定义和特性后回到之前想要实现的操作：删除最大元素和插入元素

对于删除最大元素，我们想要实现的效果是：每次删除最大元素后，经过调整，堆的根节点仍然是最大元素。

对于插入元素，我们想要实现的效果是：每次插入元素后，经过调整，堆的根节点任然是最大元素。

两个操作在我们调整之前均使得堆的有序性被破坏，而我们需要将堆的状态重新恢复，就要进行调整，这个调整的过程就叫做堆的有序化（reheapifying）。

那么我们的思路就变成这样：

删除最大元素：删除根节点——>有序化——>堆状态恢复
插入元素：插入节点——>有序化——>堆状态恢复

由此，现在我们来认识有序化，在学会有序化后，删除最大元素与插入元素的操作也就不难了。

堆的有序化

有序化过程中会有两种情况：

某个节点优先级上升（比如在堆底插入一个优先级很高的元素），就需要由下至上恢复堆
某个节点优先级下降（比如根节点替换为一个优先级较低的元素），就需要由上至下恢复堆

由下至上恢复堆（上浮，swim）

某个节点的优先级提升，它打破了原来的堆秩序，我们需要将他**上浮（swim）**至适当的位置，如此便能恢复原来的堆秩序。

首先，此节点和父节点比较，若比父节点更大，则与此父节点交换；交换后，再与新的父节点比较，若比新的父节点大，则继续交换......直至遇到比其大的父节点或成为根节点。如图所示

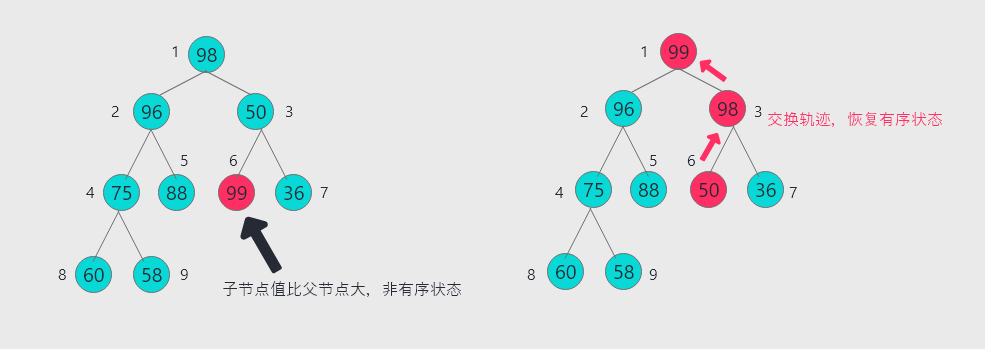
此部分的代码如下

  swim(k) {
    //上浮
    while (k > 1 && this.less(Math.floor(k / 2), k)) {
      this.exch(Math.floor(k / 2), k);
      k = Math.floor(k / 2);
    }
  }

由上至下恢复堆（下沉，sink）

某个节点的优先级下降了，它打破了原来的堆秩序，我们需要将他**下沉（sink）**至适当的位置，如此便能恢复原来的堆秩序。

在下沉的过程中，同时需要比较两个子节点的大小，选择较大者与原节点交换。

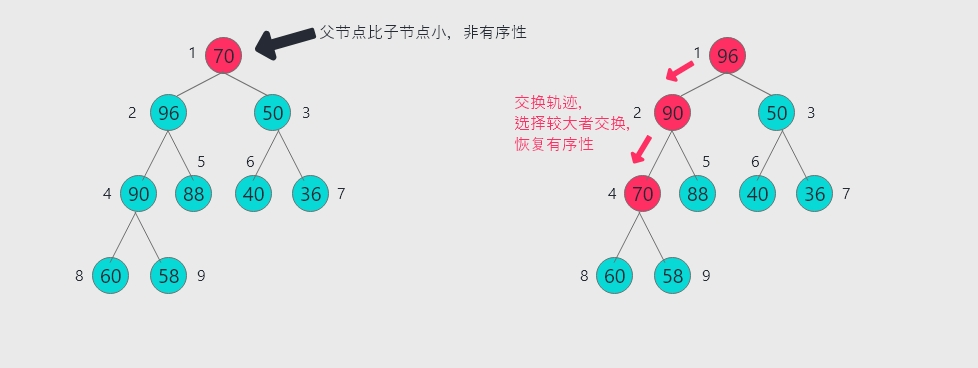
此部分代码如下

  sink(k) {
    //下沉
    while (2 * k <= this.pqIndex) { //this.pqIndex表示现指向的空位置或超出数组原容量的新位置
      let j = 2 * k;
      j < this.pqIndex && this.less(j, j + 1) ? j++ : null; //寻找两个子节点最大的
      if (!this.less(k, j)) {
        //若上面比下面都大，则下沉完成
        break;
      }
      this.exch(k, j);
      k = j;
    }
  }

插入元素与删除最大元素

在了解有序化及其上浮下沉操作后，我们把它应用在插入元素与删除最大元素之中。

对于插入元素，我们仅需把元素插入，并对其上浮即可

  insert(ele) {
    this.pq[this.pqIndex] = ele;
    this.swim(this.pqIndex); //对插入元素上浮
    this.pqIndex++;
  }

对于删除最大元素，将根节点（假设值为A）与最末位节点（假设值为B）交换，将A删除，然后对新的根节点（B）进行下沉

  delMax() {
    //删除并返回最大元素
    this.pqIndex--;
    const maxEle = this.pq[1]; //记录最大元素
    const lastEle = this.pq[this.pqIndex]; //末尾元素
    this.pq[1] = lastEle; //将末尾元素置于根节点
    this.pq[this.pqIndex] = null; //删除交换后的根节点
    this.sink(1);
    return maxEle;//返回已被删除的最大元素
  }

总结

如上基于二叉堆的优先队列，使得我们对于插入元素操作不需要超过（lgN + 1）次比较，删除最大元素操作不需要超过2lgN次比较。。在现代计算中，输入的N极大非常常见，相对于之前的重排序方案效率上可谓极大的提升。

同时，此基于二叉堆的优先队列排序可以进一步引申出堆排序。

参考资料

《算法（第4版）》

算法学习in js：基于二叉堆的优先队列

前言