论文研读 （硕）基于分层强化学习的多agent路径规划与编队方法研究

赤西沽
1,275 阅读6分钟

摘要

对于多agent的路径规划以及编队控制，提出了使用model- free 的强化学习方法。

为了避免强化学习“维度灾难”，提出分层强化学习方法。

三个key words：

  • semi MDP
  • 抽象机制
  • 经典算法：options, HAM, MAXQ

人工势场法： 构建环境的先验知识

CMAC小脑神经网络：用神经网络来加快收敛速度

CMAC神经网络具有小脑的机能，因而，被广泛应用于机器人的运动控制

背景

路径规划

路径规划：

  • 集中式规划--超级agent--适合三个数量较少的MAS

  • 分散式规划--每一个agent有传感器，有通信手段--适合我们的项目

  • 划掌握完全环境信息的全局路径规划

  • 通过传感器实时探测环境信息的局部路径规划： 人工势场法、强化学习算法、遗传算法、模糊逻辑、蚁群算法、免疫算法、神经网络 等

人工势场法

基本原理：：将agent 在未知环境中的运动认为是在一个虚拟化的抽象的人工势能场中的运动，设在目标点附近虚拟一个引力势场， 对agent 产生趋向它运动的引力，而障碍物附近有排斥的势能场，对agent 产生阻碍向其运动的排斥力。agent 的在环境中实际运动方向就是引力和排斥力的合力。

**优点：**计算量小、算法结构简单、实时性好

缺点：运动过程中易陷入局部最小值， agent 路径的目标不可达， 在局部 区域中在障碍物面前产生路径振荡（U型障碍无法逃出去）

编队控制

**主流方法: ** 跟随领航者法(leader follow)、虚拟结构法、基于行为的方法和基于图论法等

本文研究内容

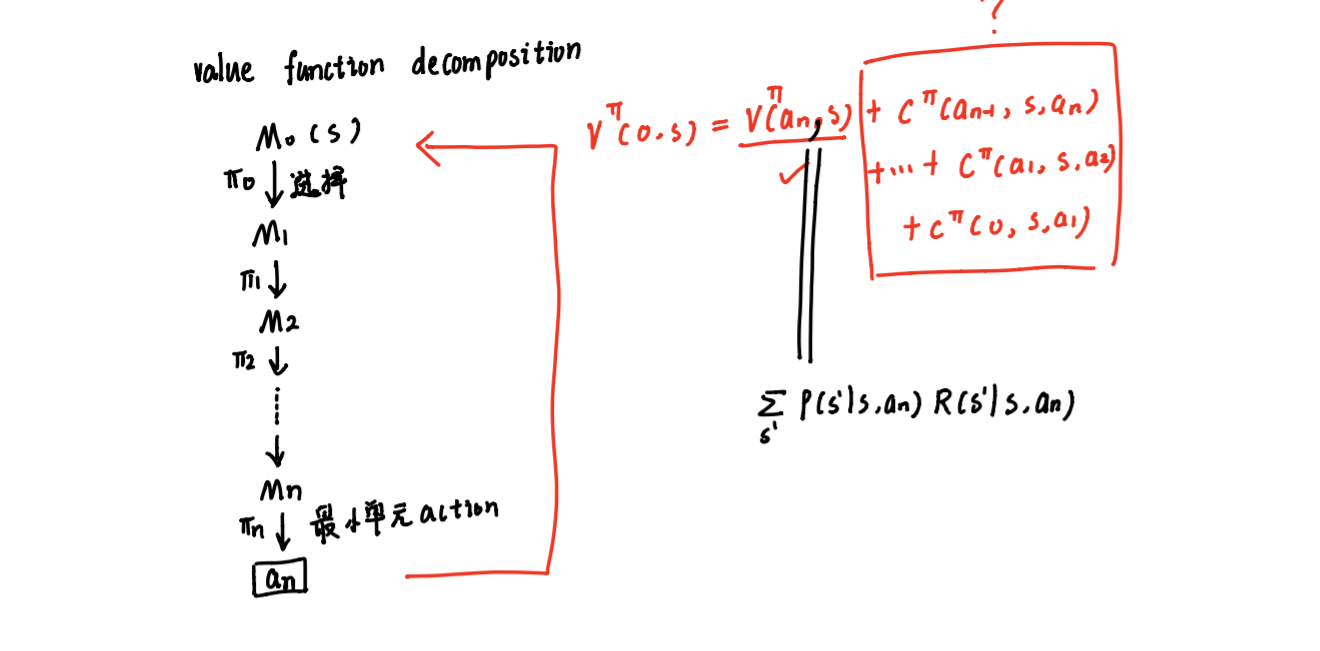
结合前一节描述的多agent 系统路径规划和编队的国内外研究现状，本文的提出了 两个基于分层强化学习的算法来解决MAS 路径规划和编队问题。一是基于人工势场及 分层强化学习的多agent 路径规划方法； 二是基于CMAC神经网络及分层强化学习多agent 编队方法。两种方法利用分层强化学习方法的无环境模型学习以及局部更新能力将策略更 新过程限制在规模较小的局部空间或维度较低的高层空间上，改进学习算法的性能； 在 路径规划问题中加入人工势场将多agent 的运行环境虚拟为一个人工势能场，根据先验 知识确定每点的势能值，它代表最优策略可获得的最大回报：在编队问题中应用神经网 络算法可以作为状态泛化方法和分层强化学习中的Q－学习方法相结合，解决连续、较 大状态空间下的强化学习问题，可以加快Q 值函数的更新速度、学习准确度更高。

分层强化学习理论基础

强化学习方法学习参数个数随状态、动作维数成指数级增长，即 “维数灾难”所困扰

克服维数灾难的方法主要有状态聚类法、有限策略空间搜索法、值函数近似法和分层强化学习四方法。

状态聚类法通过把多个相近状态聚为单一状态有效地缩减了状态空间，但缩减后的 状态空间不具备马尔可夫性质，导致强化学习系统的摆期很长或者不收敛；

有限策略空间搜索法根据可观测到的局部状态直接在有限的策略雪间中寻优， 但该方法经常陷入局 部最优，求解质量得不到保证；

值函数近似法使用一组特征基函数的线性组合来近似表示值函数，但是所需的特征只有在具备问题先验知识的前提下才可获取。

分层强化学习：

三个key words：

  • semi MDP
  • 抽象机制：对状态空间实现降维，将任务分解到抽象内部和抽象间的不同层次上分别实现， 从而每层上的学习任务仅需在低维空间中进行
  • 经典算法：options, HAM, MAXQ

半马尔可夫决策过程 SMDP

MDP过程：它的模型也是仅考虑在单个时间步中完成假设动作

SMDP模型中：可以处理需要多个时间步完成的动作

区别于MDP而言，SMDP的不同就在于两次make decision的timepoint之间的interval不是等间距且固定的。

算法区别：多了一个时间 \tau：是系统在状态S 执行动作α 后的随机等待时间

，以至于状态转移概率多了一个参数：P\left(s^{\prime}, \tau | s, a, R\right)

q-learning算法基本不变

V^{*}(s)=\max _{a \in A}\left[R(s, a)+\sum_{s, \tau} \gamma^{\tau} P\left(s^{\prime}, \tau | s, a\right) V^{*}\left(s^{\prime}\right)\right]
Q^{*}(s, a)=R(s, a)+\sum_{s, \tau} \gamma^{\tau} P(s, \tau | s q) \max _{a \in A} Q^{*}(s, a)
Q_{k+1}(s, a)=(1-\alpha) Q_{k}(s, a)+\alpha\left[r_{t}+\gamma r_{t+1}+\cdots+\gamma^{\tau-1} r_{t+\tau-1}+\gamma^{\tau} \max _{a \in A} Q_{k}\left(s^{\prime}, a^{\prime}\right)\right]

已证明SMDPQ- 学习在标准Q－学习算法的收敛条件下收敛。

分层强化学习基本算法

option

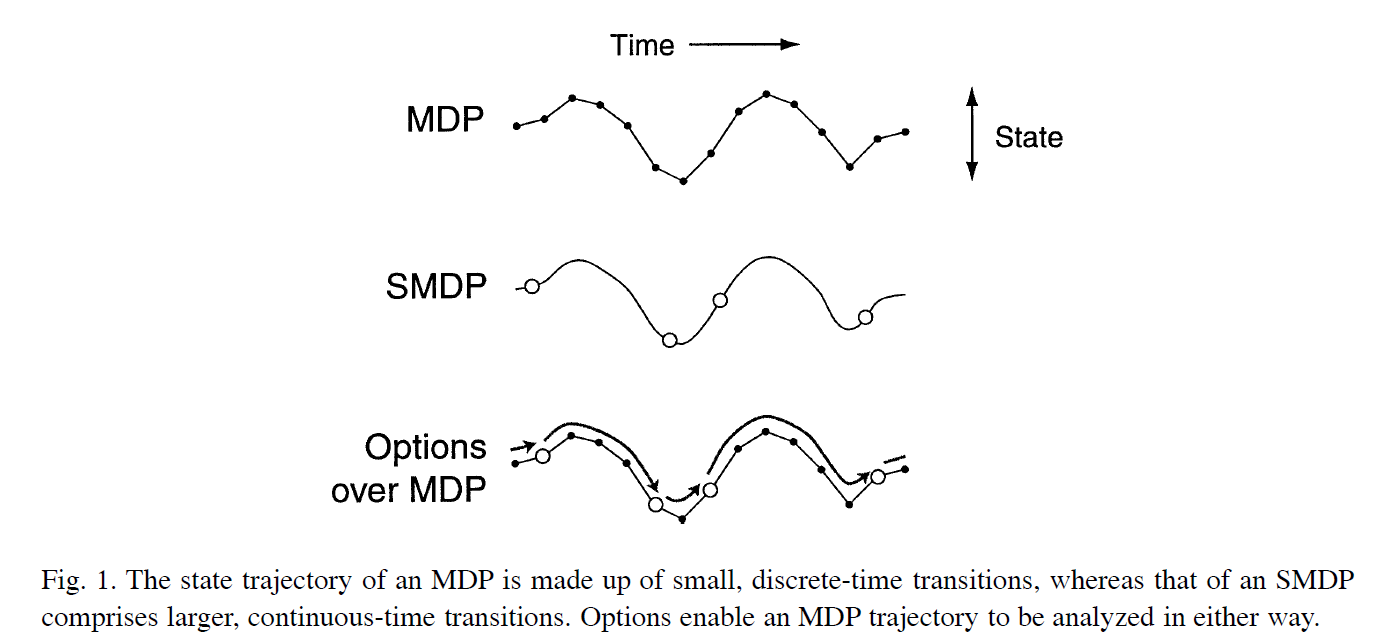
第三条轨迹是options over MDP，可以看做是我们把MDP抽象出一些间隔不均等的timepoints，得到了SMDP

（反过来看，options over MDP也可以看出我们把一个SMDP不均等的timepoints之间用Options补齐，得到了一个在均等间隔的timepoints上make decision的MDP）

通俗理解：

Options是primitive actions的generalization，是为了描述一种在时间上延展的一系列动作（temporally extended courses of action），比如吃饭需要一口一口吃一个菜一个菜夹，当然你也可以继续展开，也可以把吃饭看成一个动作。

option由三元组构成

\langle\mathcal{I}, \pi, \beta\rangle

I是Initiation的意思，是一个状态的集合（整个大MDP的state子集），代表这个option在哪些状态下是可选择的。比如说你只有在状态<饭做好了,洗过手了>等状态下的可以选择吃饭这个option。

π代表这个option的内部策略，即这个option被选择之后，真正观察到状态s时，mapping到怎样的a。比如上菜的时候，你是先吃碗里的，还是先夹锅里的。

β是termination condition，也就是什么时候终止这个option，是state到0,1之间概率的mapping。继续比如，要是菜很难吃，你是在吃5分钟掀桌子，还是吃10分钟的时候掀桌子...

option和option之间 的选择策略：

\mu: \mathcal{S} \times \mathcal{O} \rightarrow[0,1]

这个时候在一堆options里我选哪一个。其实和常规的policy类似，只是high-level而言，actions变成了options。

整个desicion的过程：

在s_t下，根据μ(s_t)选择option A，然后选择动作π_A(s_t)，转到下一个state s_t+1，继续选择动作π_A(s_t+1) ...直到option A凭termination condition终止，到达s_t+n，然后根据μ(s_t+n)再选择一个option ...如此进行。

HAM

MAX-Q

avatar
文章
阅读
粉丝