系统稳定性
在自动控制领域中,李雅普诺夫稳定性(英语:Lyapunov stability,或李亚普诺夫稳定性)可用来描述一个动力系统的稳定性。如果此动力系统任何初始条件在平衡态附近的轨迹均能维持在平衡态附近,那么可以称为在处李雅普诺夫稳定。 稳定性问题的字面意思很好理解了,那就是系统在受到扰动后,能否能有能力在平衡态继续工作。
稳定点就是系统状态不再发生变化的点
对于一个简化的倒立摆模型
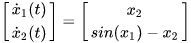
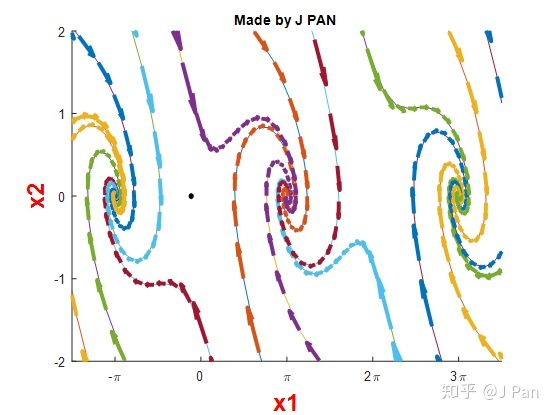
详见 zhuanlan.zhihu.com/p/58738073
李雅普诺夫第一法
非线性系统在平衡态附近线性化,然后讨论线性化系统的特征值分布来研究原非线性系统的稳定性问题。这种方法,称之为第一法,也叫间接法,比较麻烦,但是比较适用,这里我就不多讲了,论文主要用的是第二法。
李雅普诺夫第二法
第二法就比较天才了,来源于一个朴素的想法:稳定的系统能量总是不断被耗散的,李雅普诺夫通过定义一个标量函数 (通常能代表广义能量)来分析稳定性。这种方法的避免了直接求解方程,也没有进行近似线性化,所以也一般称之为直接法。如果 标量函数
满足:
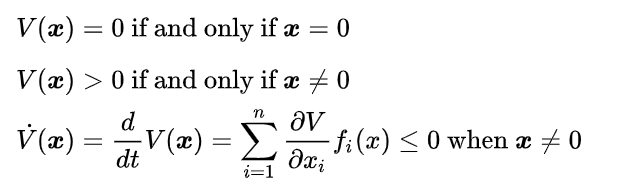
则称系统在李雅普诺夫意义下是稳定的
这个 在综述论文中就是我们的value function