什么是二次型最优控制

要达到最优控制，也就是我们要把cost function达到最小值

二次型最优控制的cost function是用这种类似的思想推出来的：

我们定义cost funcion如下：

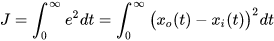
为实际状态，为期望状态

为简单起见，我们先假设期望状态为零，即

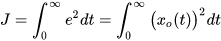
向量表示

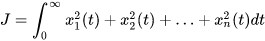
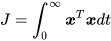
这就是一种简单的二次型函数，因为变量的最高次数是2。

扩展一下这个式子，将单位矩阵扩展为对角矩阵

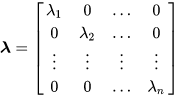
再扩展为一般矩阵

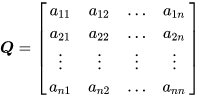
相当于是给每一个变量误差都取一个权重

但无论怎么扩展，展开的函数最高次数都是2次，因此我们把这种类型的函数统称为二次型函数。

对于一个完整的二次型最优控制的代价方程：

我们的目标是求损失J最小

线性二次型调节控制(LQR)是一个特殊的有限边界MDP模型，所以我们可以用强化学习的方法来解这个问题 LQR的目标就是找到一组控制量u0,u1,...使 x0,x1...足够小，即系统达到稳定状态； ->见稳定性分析文章 u0,u1,...足够小，即花费较小的控制代价。

(忽略一下)

泛函

简单的说， 泛函就是定义域是一个函数集，而值域是实数集或者实数集的一个子集，推广开来，

泛函就是从任意的向量空间到标量的映射。也就是说，它是从函数空间到数域的映射。

设{y}是给定的函数集，如果对于这个函数集中任一函数y(x) 恒有某个确定的数与之对应，记为П(y(x))，则П(y(x))是定义于集合{y(x)}上的一个泛函。

泛函定义域内的函数为可取函数或容许函数， y(x) 称为泛函П的变量函数。

泛函П(y(x))与可取函数y(x)有明确的对应关系。泛函的值是由一条可取曲线的整体性质决定的。

泛函也是一种“函数”，它的独立变量一般不是通常函数的“自变量”，而是通常函数本身。泛函是函数的函数。由于函数的值是由自变量的选取而确定的，而泛函的值是由自变量函数确定的，故也可以将其理解为函数的函数

泛函的自变量是函数，泛函的自变量称为宗量。 简言之，泛函就是函数的函数。