论文研读 Optimal and Autonomous Control Using Reinforcement Learning: A Survey

如何读综述：

首先从摘要读起，然后读结论。如果你能读懂摘要和结论，那么再开始读introduction

在读introduction的时候，在脑子里尽量形成一些框架式的结构，如综述所阐述问题的结构是什么样的、文章的组织结构是什么样的。

一篇好综述的introduction部分，其中所引用的文献往往是这个领域中具有标志性意义的文献，也就是通常所说的经典文献。

摘要和结论

这篇综述回顾了一些RL在optimal control problems的算法和应用。

从DT system和CT system两个角度来介绍

这里的optimal control problems指的是非线性系统的控制问题，以及特殊情况的LQ最优控制问题（linear quadratic二次型），包括：

optimal regulation problem = 最优调节问题

optimal $H_2$ 范数 and $H_\infty$ 范数 control problems

optimal tracking control problem=最优跟踪问题

还讲了

Nash problem一些博弈论的问题

graphical games problem(多智能体问题)

介绍了一些强化学习用在控制方面的新的方向：

off-policy RL for both CT and DT systems

DRL for both CT and DT systems

一、introduction

以前的optimal control的一些成熟的文献介绍 [1]-[6]

讲了两个重要的优化问题的原理：

庞特里亚金最大化原理（Pontryagin's maximum principle）
DP 原理

用以上两个原理的经典的方法解决optimal control问题是offline 的，并且是需要知道完整的dynamic system model的，所以他们很难应用在uncertainties and changes 的 dynamics中的。

$online$ : step-by-step update,例如TD;相反MC是episode by episode ,所以是offline的

强化学习（rl）便应运而生，在控制领域，通常叫他为ADP(approximate DP或者是adaptive Dp)

具体开始介绍本文主要用的RL方法：

policy evaluation

policy improvement

两者构成了PI框架(policy iteration)以及VI框架(value iteration)

PI框架在optimal control 问题上用的比较多，这篇文章主要也是用PI框架来解决问题。

两者区别：

PI：

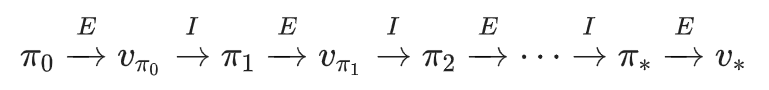
VI:

相比于PI算法，每次迭代中又都包含一个「策略估计（policy evaluation）」迭代，这种扫描整个状态集的方法确保精确性

其实我们可以考虑不做这么精准的「估计（evaluation）」，而是每一步（每次处理一个状态）都同步进行 evaluation 和 improvement，也不再以策略是否稳定为标准，而是看总的上界是否收敛。

具体更新过程如下图所示：

RL在控制领域的主要应用

optimal regulation (优化调度)
optimal tracking control (追踪轨迹，就是给定一条期望的轨迹，让agent自己学会如何以最优控制的形式通过这条轨迹)
多智能体协同

最后RL可以分成两类on-policy 和 off-policy

off-policy的好处:

data effcient
offpolicy algorithms take into account the effect of probing noise needed for exploration (考虑了探测所需的探测噪声的影响) ???? （我觉得是因为offpolicy是注重exploration的方法，所以考虑了探测所需的探测噪声的影响）

off-policy的结构图:

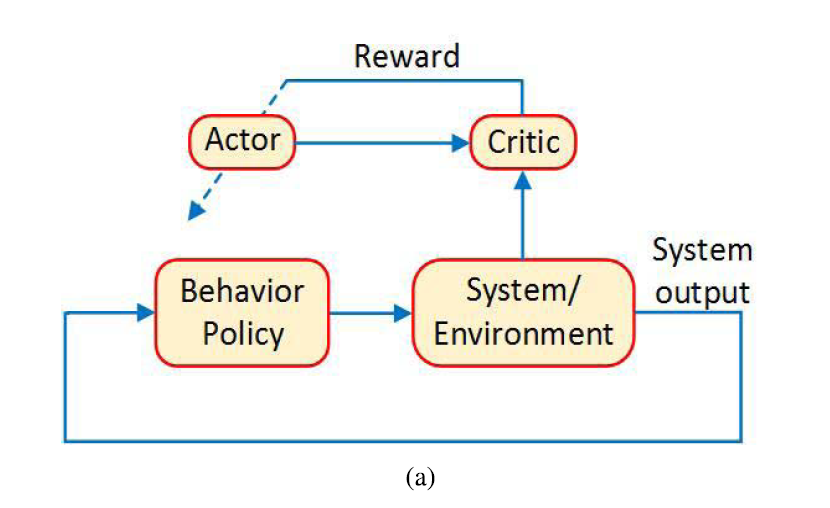
用behavior policy 选择action与环境进行交互

on-policy的结构图:

Actor的策略直接选择action与环境进行交互

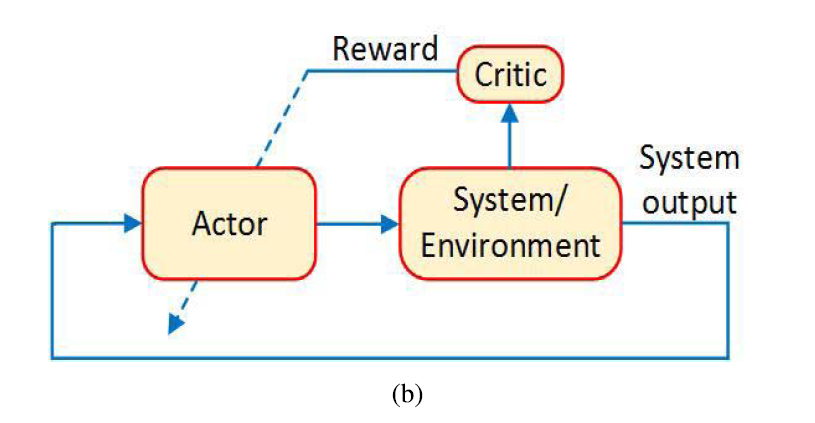
二、optimal control of DT systems and online solutions

we present the optimal control problems for discrete-time (DT) dynamical systems and their online solutions using RL algorithms. This section includes optimal regulation problem, tracking control problem, and H∞ problem for both linear and nonlinear DT systems.

我今天主要讲一下optimal regulation problem的一些内容。

首先介绍一下线性系统的一些概念，因为之前我们没有系统的学过：

[见线性系统纸质笔记]

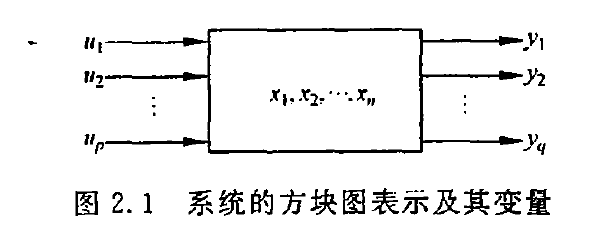
非线性时不变系统：


x(t+1)=f(x(t),u(t)) 
y(t+1)=g(x(t),u(t))

f和g向量中至少一个组成元的 x(t) 和 u(t) 为非线性关系

论文给出的非线性时不变系统：

\color{red}{x(k+1)=f(x(k))+g(x(k))u(k)}
\\
\color{red}{y(k)=l(x(k))}
\tag{1}

$x(k)=state$

$u(k) =input=policy$

$y(k)=output=环境的反馈$

目标：找到一个最优input/policy $u(k)^*$

$\color{red}{?}$ 假设前提：

f (0) = 0 and f (x(k)) + g(x(k))u(k) is locally Lipschitz(利普希茨连续条件)
and the system is stabilizable.

-> 可以保证上述具有有限初始条件的system有唯一解x(t)

A. optimal regulation problem

goal : design an optimal control input(最优policy) to stabilize the system in (1) while minimizing a predefined(预先定义的) cost functionl.

[二次型最优控制介绍]

什么是二次型最优控制

线性二次型最优控制也就是LQ问题，L指的是线性系统，Q指的是性能指标函数限定为二次型函数及其积分

举个简单例子，要达到最优控制，也就是我们要把cost function达到最小值

我们定义cost funcion如下：

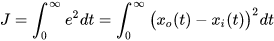
$x_{o}(t)$ 为实际状态， $x_{i}(t)$ 为期望状态

为简单起见，我们先假设期望状态 $x_{i}(t)$ 为零，即

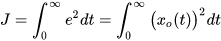
向量表示

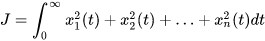
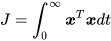
这就是一种简单的二次型函数，因为变量的最高次数是2。

（扩展一下这个式子，将单位矩阵扩展为对角矩阵

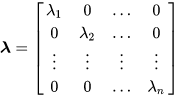
再扩展为一般矩阵

）

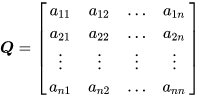
相当于是给每一个变量误差都取一个权重

但无论怎么扩展，展开的函数最高次数都是2次，因此我们把这种类型的函数统称为二次型函数。

对于一个完整的二次型最优控制的代价方程：

我们的目标是求损失J最小

线性二次型调节控制(LQR)是一个特殊的有限边界MDP模型，所以我们可以用强化学习的方法来解这个问题 LQR的目标就是找到一组控制量u0,u1,...使 x0,x1...足够小，即系统达到稳定状态； ->见稳定性分析文章 u0,u1,...足够小，即花费较小的控制代价。

energy-related cost functionl: $J=\sum_{i=0}^\infty U(x(i),u(i))\equiv\sum_{i=0}^\infty (Q(x)+u^T(i)Ru(o))$

$Q，R都是正定矩阵$

$V(x(k))=\sum_{i=0}^∞ U(x(i),u(i))$

$U(x(i),u(i))$ ==reward function (为负值的reward,能量损失)

$V(x(k))$ ==value function

贝尔曼方程:

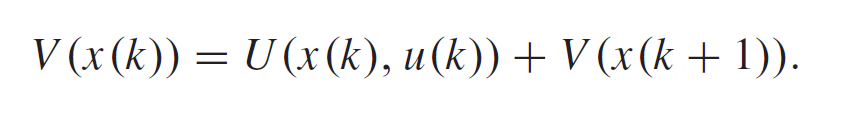
Hamiltonian（汉密尔顿）距离:

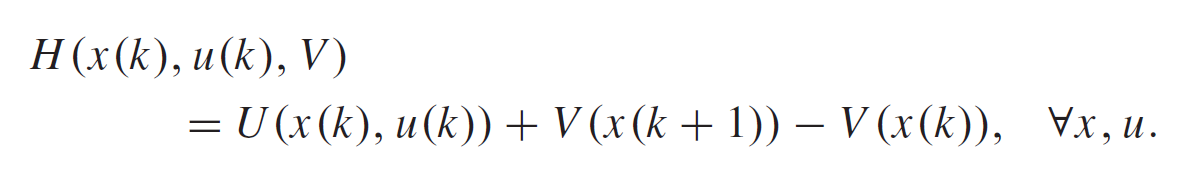
$H(x(k), u(k), V)==$ TD error

由Bellman optimality principle得到optimal value function (DT HJB equation,哈密顿-雅可比-贝尔曼方程（Hamilton-Jacobi-Bellman equation，简称HJB方程）):

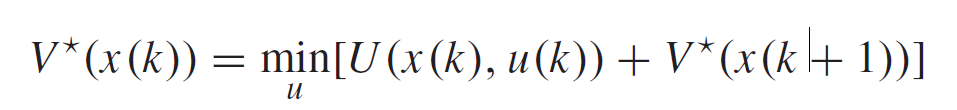
梯度下降法进行更新找到最优 $u(x(k))$

$\color{red}{这整个过程是动态规划的求解过程，需要知道完整的系统动力学知识。}$

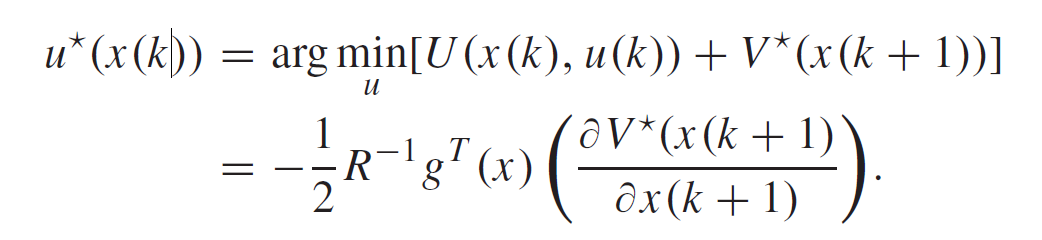
以上的推导不太完整，我在参考文献一篇文章中找到了比他详细一点的推导

论文研读 DT Nonlinear HJB Solution Using ADP: Convergence Proof

$V\left(x_{k}\right)=\sum_{n=k}^{\infty} Q\left(x_{n}\right)+u^{T}\left(x_{n}\right) R u\left(x_{n}\right)$

（根据某些条件）可以写成

$V\left(x_{k}\right)=x_{k}^{T} Q x_{k}+u_{k}^{T} R u_{k}+\sum_{n=k+1}^{\infty} x_{n}^{T} Q x_{n}+u_{n}^{T} R u_{n}$ $=x_{k}^{T} Q x_{k}+u_{k}^{T} R u_{k}+V\left(x_{k+1}\right)$

DT HJB equation：

$V^{*}\left(x_{k}\right)=\min _{u_{k}}\left(x_{k}^{T} Q x_{k}+u_{k}^{T} R | u_{k}+V^{*}\left(x_{k+1}\right)\right)$

we require the boundary condition V (x = 0) = 0 so that V (xk) serves as a Lyapunov function

因为满足Lyapunov第二法，这里简单介绍一下李雅普诺夫稳定性

系统稳定性

在自动控制领域中，李雅普诺夫稳定性（英语：Lyapunov stability，或李亚普诺夫稳定性）可用来描述一个动力系统的稳定性。如果此动力系统任何初始条件在平衡态附近的轨迹均能维持在平衡态附近，那么可以称为在处李雅普诺夫稳定。

稳定性问题的字面意思很好理解了，那就是系统在受到扰动后，能否能有能力在平衡态继续工作。

稳定点就是系统状态不再发生变化的点

李雅普诺夫第一法

非线性系统在平衡态附近线性化，然后讨论线性化系统的特征值分布来研究原非线性系统的稳定性问题。这种方法，称之为第一法，也叫间接法，比较麻烦，但是比较适用，这里我就不多讲了，论文主要用的是第二法。

李雅普诺夫第二法

第二法就比较天才了，来源于一个朴素的想法：稳定的系统能量总是不断被耗散的，李雅普诺夫通过定义一个标量函数 $V(\boldsymbol{x})$ （通常能代表广义能量）来分析稳定性。这种方法的避免了直接求解方程，也没有进行近似线性化，所以也一般称之为直接法。如果标量函数 $V(\boldsymbol{x})$ 满足：

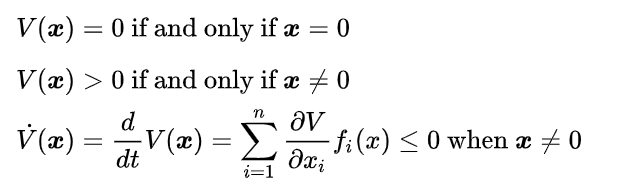
则称系统在李雅普诺夫意义下是稳定的

这个 $V(\boldsymbol{x})$ 在综述论文中就是我们的value function

~~$u^{*}$ 满足first-order necessary~~ ~~condition（优控制问题的一阶必要性条件），所以~~对等式右边求梯度

$\frac{\partial\left(x_{k}^{T} Q x_{k}+u_{k}^{T} R u_{k}\right)}{\partial u_{k}}+\frac{\partial x_{k+1}}{\partial u_{k}} \frac{\partial V^{*}\left(x_{k+1}\right)}{\partial x_{k+1}}=0$

然后 $u^{*}$ 沿着梯度方向更新

$u^{*}\left(x_{k}\right)=\frac{1}{2} R^{-1} g\left(x_{k}\right)^{T} \frac{\partial V^{*}\left(x_{k+1}\right)}{\partial x_{k+1}}$

B.special case

DT linear systems:

$x(k+1)=A x(k)+B u(k) \quad y(k)=C x(k)$

$V(x(k))=x^{T}(k) P x(k), \quad \forall x$

无限时间LQ问题的最优解,课本给出了结论，证明过程我还看不懂

$P A+A^{\top} P+Q-P B R^{-1} B^{\mathrm{T}} P=0\tag{2}$

结论6. 39 ［无限时间LQ问题最优解］给定无限时间时不变LQ调节问题，组成对应的矩阵黎卡提代数方程(2)，解阵P为n×n正定对称阵。则u* (t)为最优控制的充分必要条件是具有形式：

$u^{*}(t)=-K^{*} x^{*}(t), \quad K^{*}=R^{1} B^{\mathrm{T}} P$

论文对应的矩阵黎卡提代数方程和最优控制的解如下：

黎卡提方程是最简单的一类非线性方程。形如y'=P(x)y^2+Q(x)y+R(x)的方程称为黎卡提方程。

DT HJB becomes the DT algebraic Riccati equation (DARE)

$Q-P+A^{T} P A-A^{T} P B\left(R+B^{T} P B\right)^{-1} B^{T} P A=0$

$u^{\star}(k)=-\left(R+B^{T} P B\right)^{-1} B^{T} P A x(k), \quad \forall x$

C. Approximate Solution Using RL

HJB方程很难解，甚至是不可能用解析方法求解的，所以我们需要近似它的解。

之前提到的HJB方程和DARE要求system dynamics（系统动力学）的完整知识。

下面的PI算法用动态规划方法解出最优控制u

1) Offline PI Algorithm

offline解 DT-HJB方程，需要完整的system dynamics的知识

PI：在状态空间估计状态值函数，然后提升一次policy，不断循环这个过程直到收敛

在那篇论文中有一个大篇幅来介绍如何证明PI迭代的收敛性，可以去看看，虽然收敛性得到了保证，但是 ①these equations are difficult to solve for general nonlinear systems， ②而且需要知道systems danamic

所以我们得用函数近似的方法来解

2) Actor and Critic Approximators

现在来讲更有效的近似的方法来求解最优控制问题

使用vi迭代的online方法（PI是offline的）

critic NN 估计如下value值（如下是动态规划的式子）

$\begin{aligned} V_{i+1}\left(x_{k}\right) &=\min _{u}\left(x_{k}^{T} Q x_{k}+u^{T} R u+V_{i}\left(x_{k+1}\right)\right) \\ &=x_{k}^{T} Q x_{k}+u_{i}^{T}\left(x_{k}\right) R u_{i}\left(x_{k}\right)+V_{i}\left(f\left(x_{k}\right)+g\left(x_{k}\right) u_{i}\left(x_{k}\right)\right) \end{aligned}$

actor NN 估计如下的u值（如下是动态规划的式子）

$\begin{aligned} u_{i}\left(x_{k}\right) &=\arg \min _{u}\left(x_{k}^{T} Q x_{k}+u^{T} R u+V_{i}\left(x_{k+1}\right)\right) \\ &=\arg \min _{u}\left(x_{k}^{T} Q x_{k}+u^{T} R u+V_{i}\left(f\left(x_{k}\right)+g\left(x_{k}\right) u\right)\right) \\ &=\frac{1}{2} R^{-1} g\left(x_{k}\right)^{T} \frac{\partial V_{i}\left(x_{k+1}\right)}{\partial x_{k+1}} \end{aligned}$

即

$\hat{V}_{i}(x)=\sum_{j=1}^{L} w_{v i}^{j} \phi_{j}(x)=W_{V i}^{T} \phi(x)$

$\hat{u}_{i}(x)=\sum_{j=1}^{M} w_{u i}^{j} \sigma_{j}(x)=W_{u i}^{T} \sigma(x)$

$\phi_{j}(x), \sigma_{j}(x)$ 是 激活函数（activation functions）

之前说了V函数是李雅普诺夫函数，如果李雅普诺夫函数是对称的正定的，就可以要求critic神经网络的激活函数是对称的，即。φj (x) =φj (−x)。

然后把这两个用权重表示的式子代回到动态规划的HJB方程中，可以得到权重的更新式：

$\hat{W}_{c(j+1)}^{l+1}=\hat{W}_{c(j+1)}^{l}-\alpha_{1} \phi_{c}(x(k))\left(\left(\hat{W}_{c(j+1)}^{l}\right)^{T} \phi_{c}(x(k))\right.$ $\left.-U\left(x(k), \hat{u}_{j}(k)\right)\right)$

$\begin{aligned} \hat{W}_{a(j+1)}^{l+1}=& \hat{W}_{a(j+1)}^{l}-\alpha_{2} \sigma_{a}(x(k)) \\ & \times\left(2 R\left(W_{a(j+1)}^{l}\right)^{T} \times \sigma_{a}(x(k))\right.\\ &\left.\quad+g(x(k))^{T} \frac{\partial \phi(x(k+1))}{\partial x(k+1)} \hat{W}_{c(j+1)}\right)^{T} \end{aligned}$

然后就通过两个神经网络不断更新各自的权重，最后就可以很好的来近似状态值函数以及policy u了。