数据结构与算法(十二) 红黑树

Rui4u君
1,054 阅读6分钟

红黑树

在阅读红黑树之前要弄明白B树，做到想到红黑树，心中有B树。没有弄明白的可以看我上一个文章

数据结构与算法(十一) 红黑树

红黑树例子

红黑树也是一种自平衡二叉搜索树

以前也叫做平衡二叉B树

红黑树必须满足一下5个性质

  • 节点是有颜色的Red/Black
  • 根节点必须是Black
  • 叶子节点必须是Black
    • 红黑树的叶子节点会自动将度为0 或者度为1的节点的度自动补充为2，补充的节点称之为外部节点
      • 外部节点是空想出来的，代码中不会实现
  • red节点的子节点都是black色
  • 从任意一节点到叶子节点的所有路径包含的black节点数目相同
    • 这里说的叶子节点包含假想出来的叶子节点

一、判断下面是否为红黑树

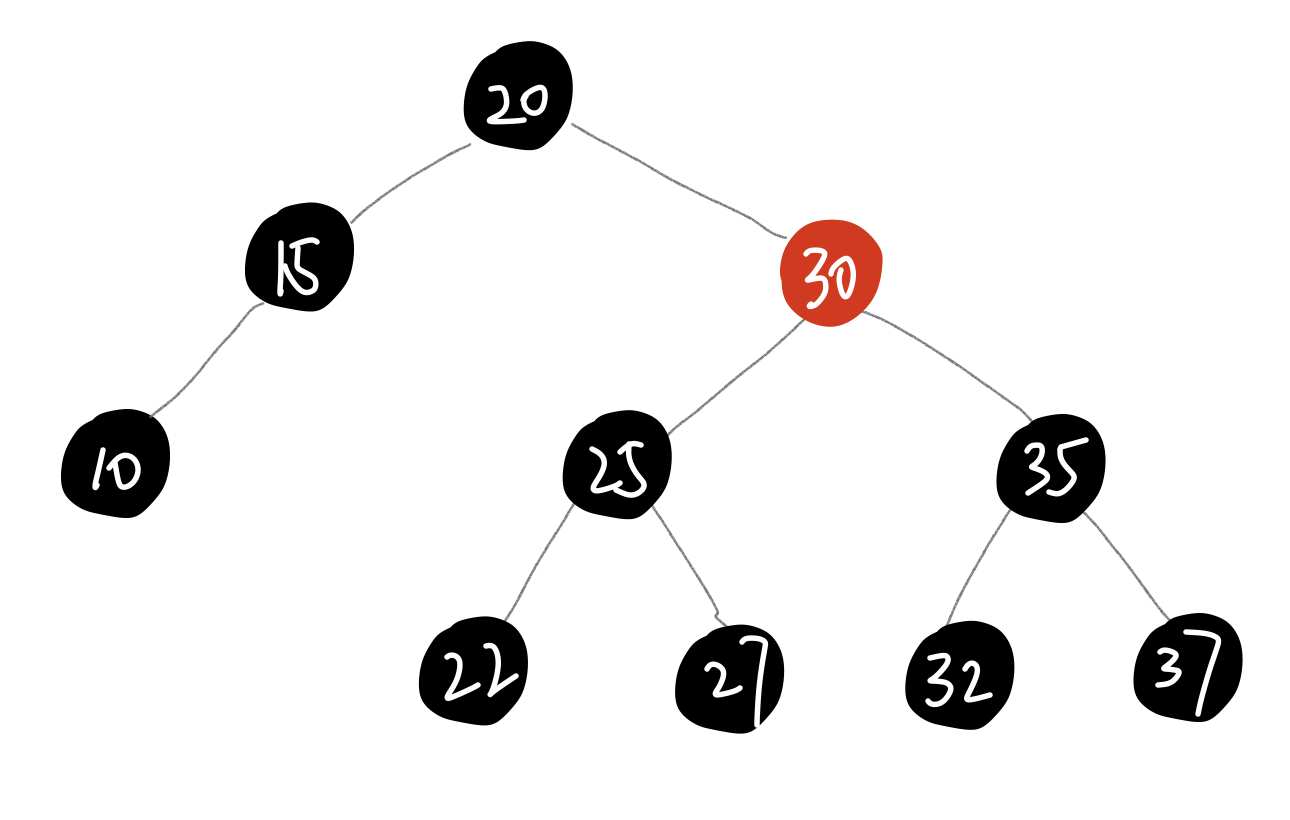
判断是否为红黑树

  • 不是

    满足

    • 节点是有颜色的Red/Black
    • 根节点必须是Black
    • 叶子节点必须是Black
      • 红黑树的叶子节点会自动将度为0 或者度为1的节点的度自动补充为2，补充的节点称之为外部节点
        • 外部节点是空想出来的，代码中不会实现
    • red节点的子节点都是black色

  • 不满足

    • 从任意一节点到叶子节点的所有路径包含的black节点数目相同

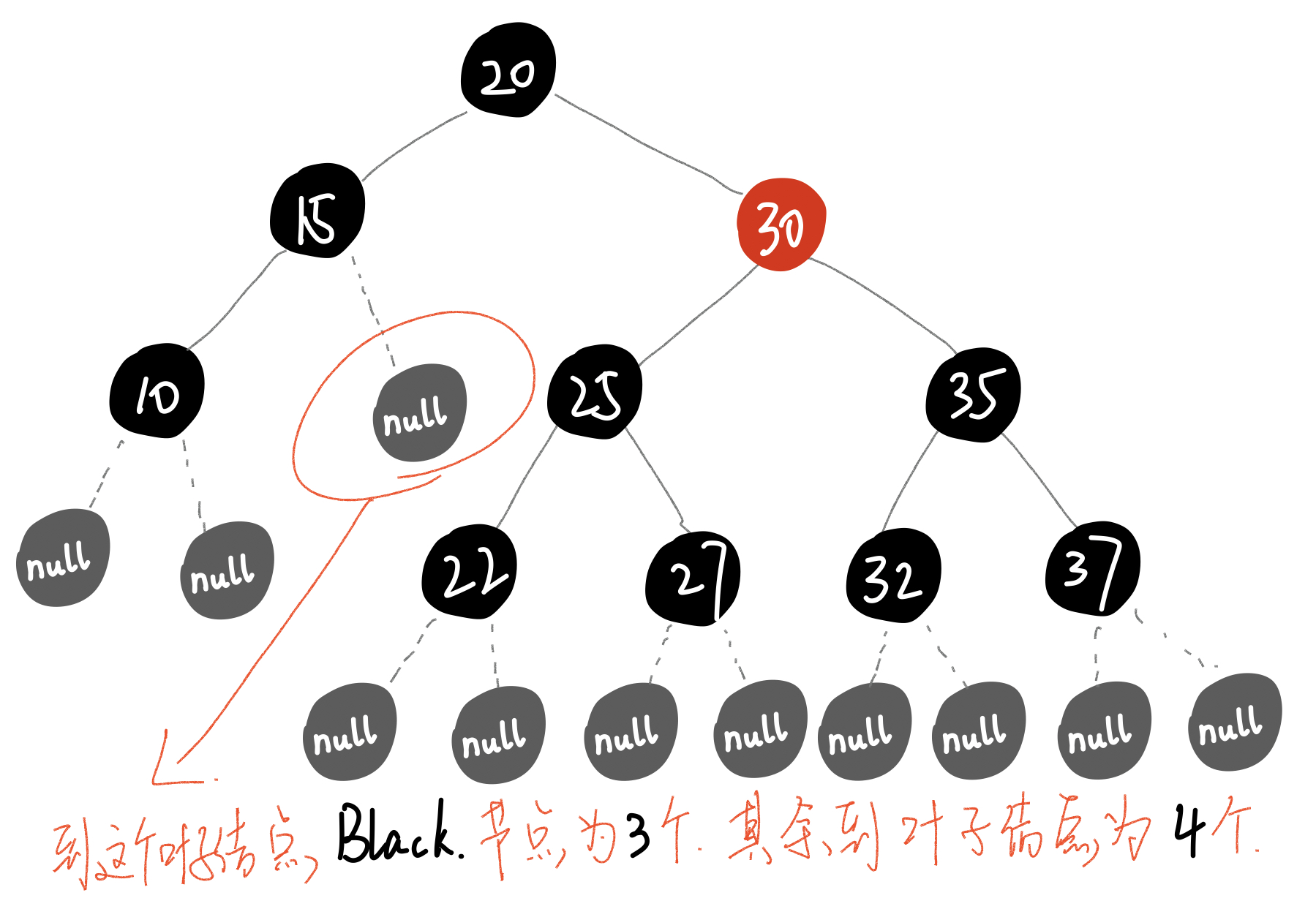
解释不是红黑树

二、红黑树的等价变换

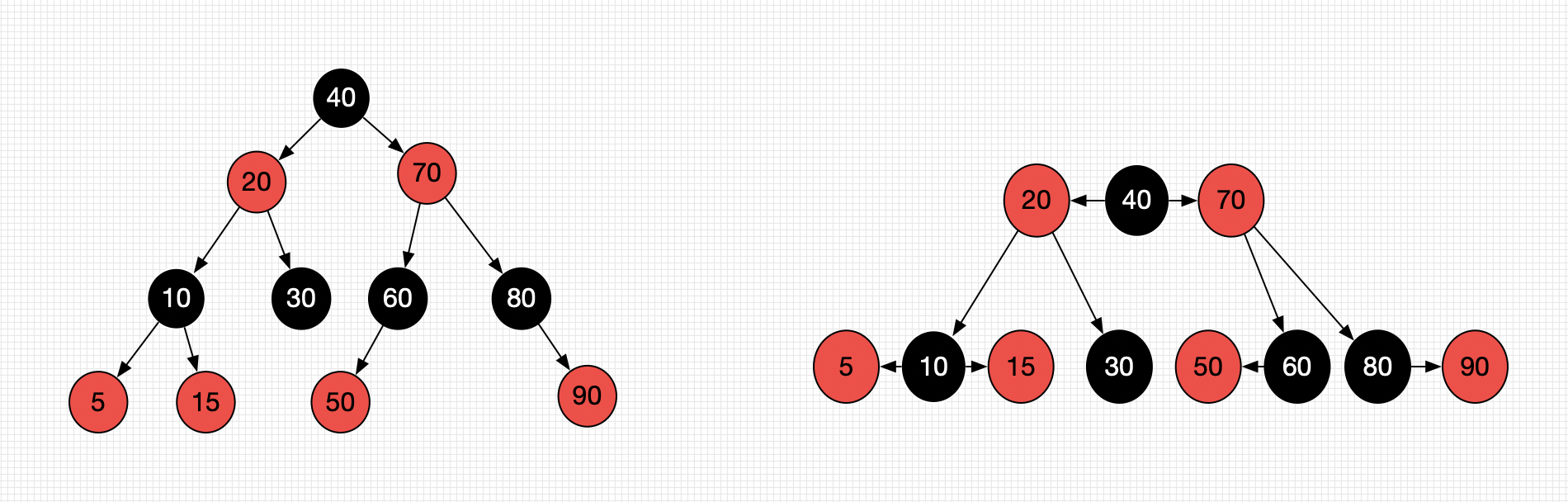
红黑树的等价变换

  • 红黑树和4阶B树具有等价性

    • Black节点与他的Red子节点融合在一起，就形成一个B树节点

  • 红黑树的Black节点个数与4阶B树的节点总数相等

三、红黑树的操作

1、添加

  • 想像成4阶B树
    • 添加操作都在叶子节点中。
    • 4阶B树所有节点的元素个数为 1 <= x <= 3。
  • 建议新添加的节点默认为Red （这样能更快的满足红黑树的性质）。
  • 根节点默认为Black。

所有的添加情况如下图所示

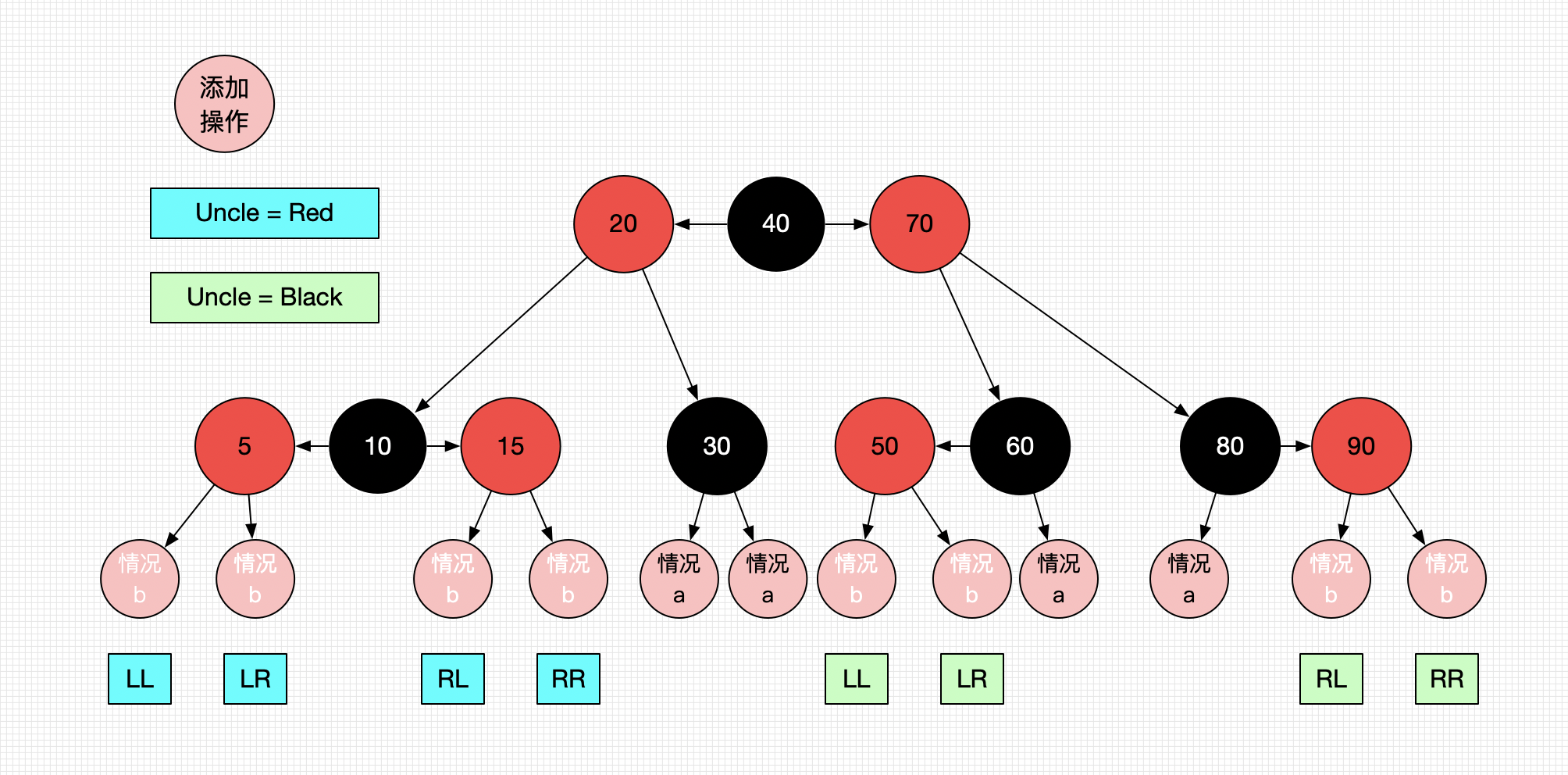
添加时所有的情况

添加情况处理：

a、当parent为black的情况，直接添加，无需特殊处理。（4种情况）
b、当parent为Red的情况。有以下几种情况（8种）
1、当uncle节点为Black时

  • RR/LL情况

    • 先对parent染成黑色，在对grand染红（染色的意义是在与让后面旋转后parent的节点为黑色，parent的子节点为黑色）
    • 当RR/LL情况的时候，需要对其进行左旋转/右旋转。（grand变成parent的子节点）。

  • LR\RL情况

    • 将自己染成Black，grand染成Red 。（染色的意义是进行后面的双旋转操作后自己成为parent节点，规定partent的节点为黑色，parent的子节点（原来的parent和grand）为Red。）。
    • 进行双旋转
      • LR:parent左旋转，grand右旋转。
      • RL:parent右旋转，grand左旋转。
2、当uncle节点为Red时

当uncle为Red的时候，红黑树对比4阶B树会发生上溢操作。

  • 将parent、uncle染成Black。（为了单独为一个节点做准备）。
  • 将grand向上合并
  • 将grand染成Red。当做是新节点进行处理。（递归，递归的代码只是染色，而旋转操作只做了1遍）
  • 情况如下图所示:

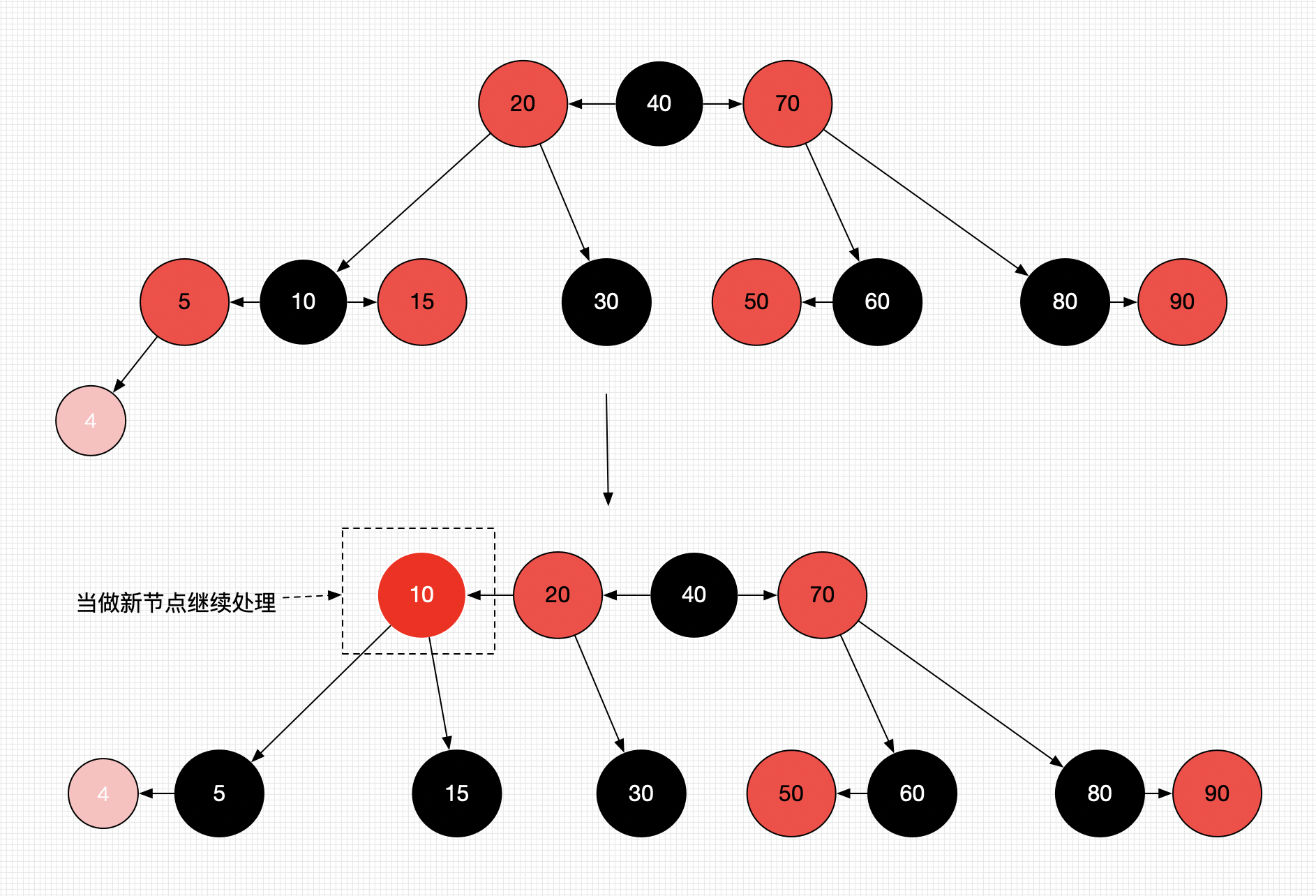
8中DoubleRed情况

2、删除

在B树中真正删除的元素都在叶子节点（若不是叶子节点，其前驱或者后继都为叶子节点，所以在替换后删除的仍然为叶子节点。 如果删除的是20，前驱15仍然是叶子节点）。

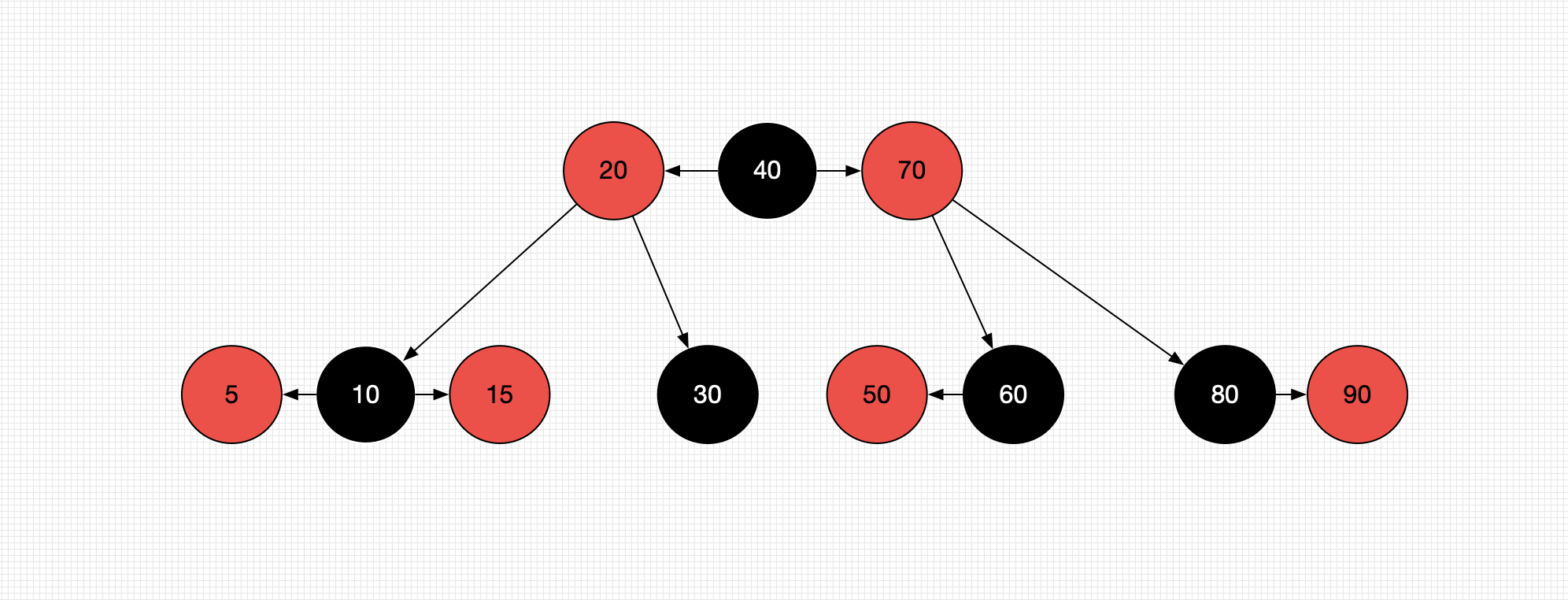
删除操作示例图

添加情况处理：

a、当删除的是Red节点的时候
  • 可以直接删除 无需其他操作
b、删除Black节点的时候

  • 当拥有2个Red子节点的black节点

    • 不可能直接删除、因为平衡二叉树要找到2个度节点的前驱或者后继、替换后删除的是前驱或者后继。（所以不用考虑这个情况）。

  • 当拥有1个Red子节点的black节点

    • 判断条件：用代替的子节点是Red
    • 将替代的的子节点染成Black
    • 情况如下图所示(删除60）

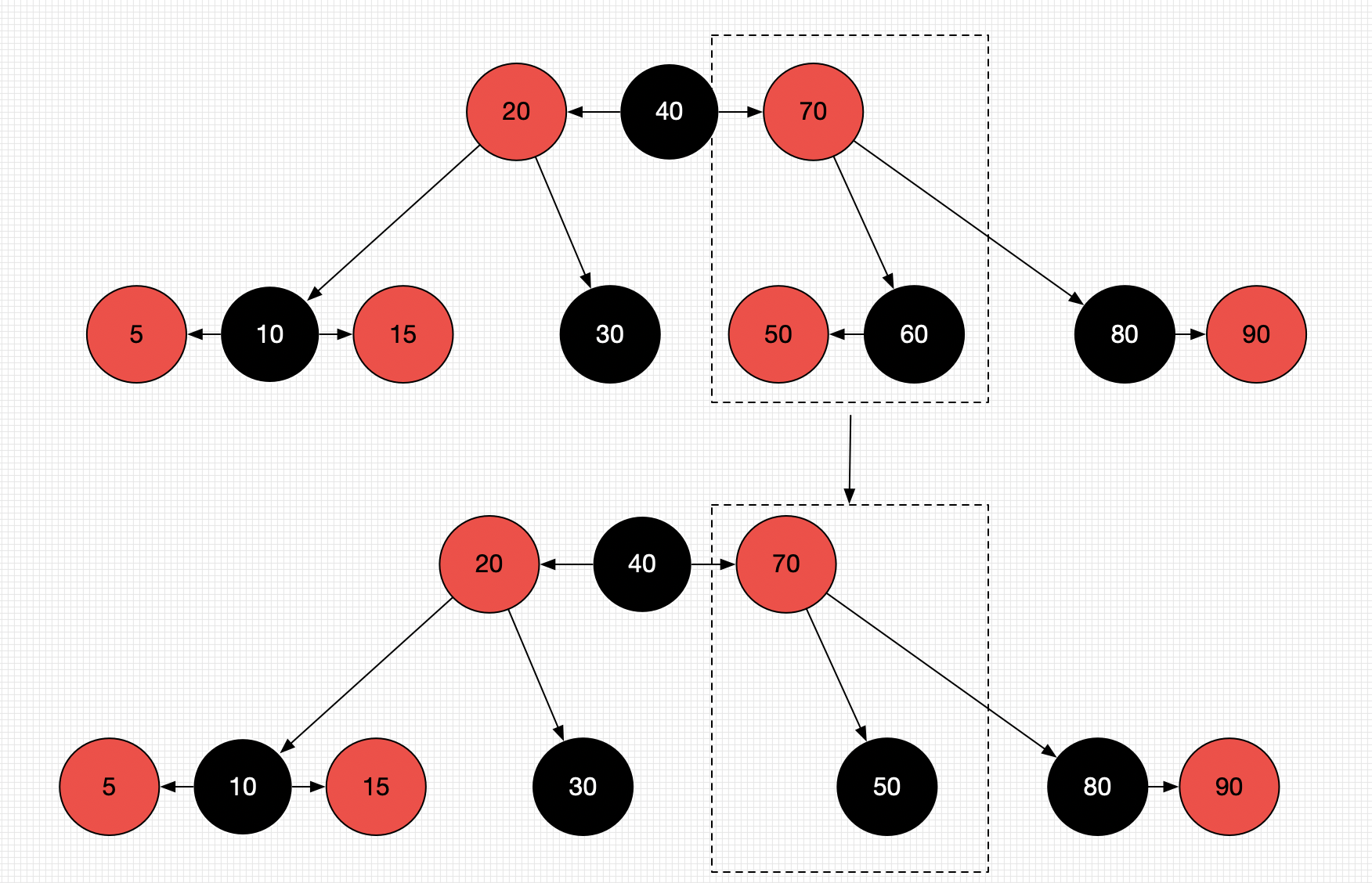
删除情况1

  • Black叶子节点

    • 如果Black叶子节点的兄弟节点为Black

      • 兄弟节点有红色节点
        • 叶子节点被删除后、可能导致B树下溢（删除33节点）
        • 进行旋转操作(LL/RR/RL/LR)，旋转之后中心节点继承parent的颜色。 （下图10继承20颜色）
        • 旋转之后左右节点染色为Black (10的字节点)。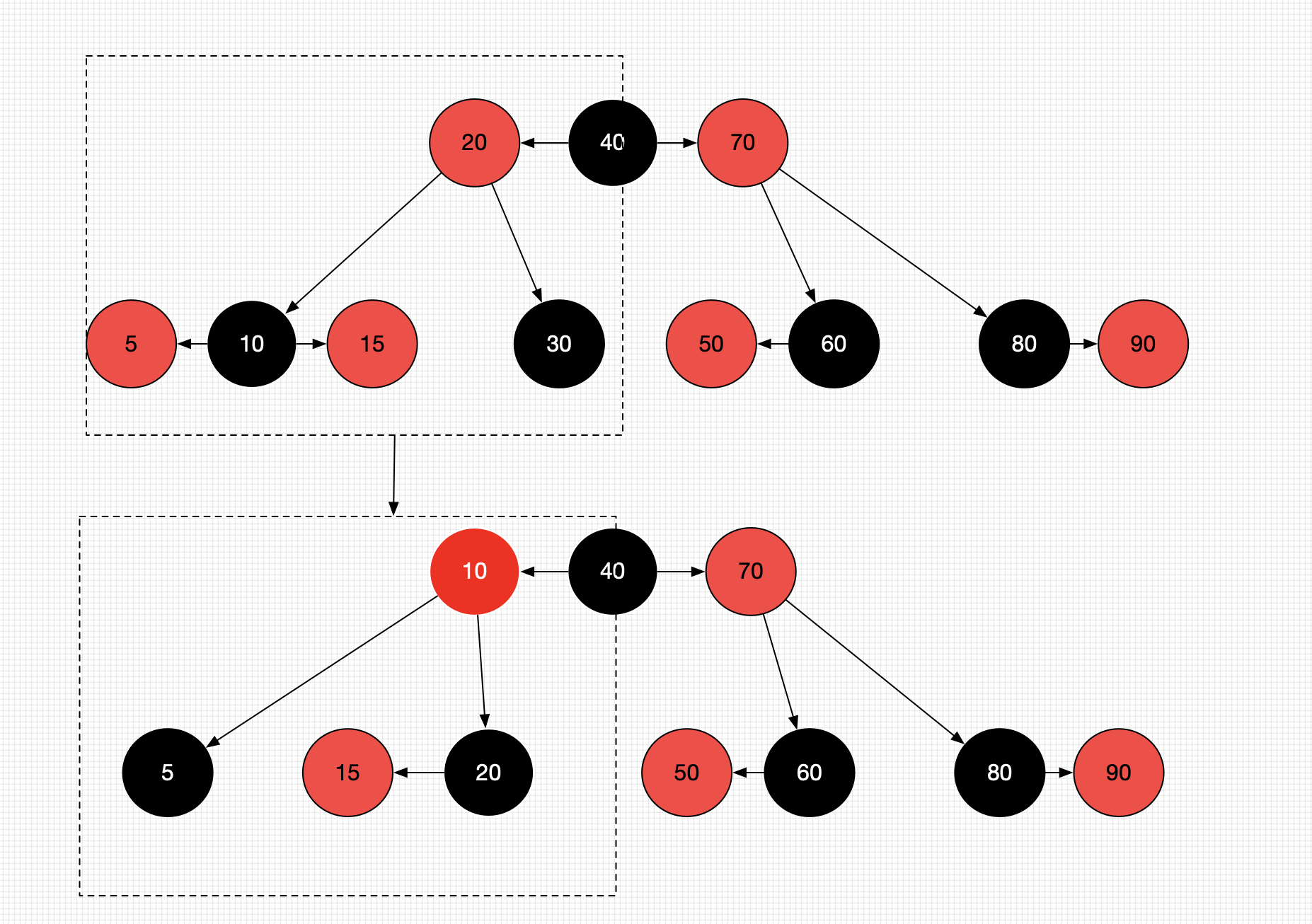
        • 删除操作下溢
      • 兄弟节点没有红色节点
        • 将兄弟节点染Red、parent节点染Black 既可。
          • 如果parent为Black, 会导致下溢，只需要把parent当做被删除的节点处理既可（递归）实验可得 递归次数小于三次。(下图中如果40的超级节点上只有40 没有20和70，那会发生下溢，只需要将40当做被删除的节点既可)。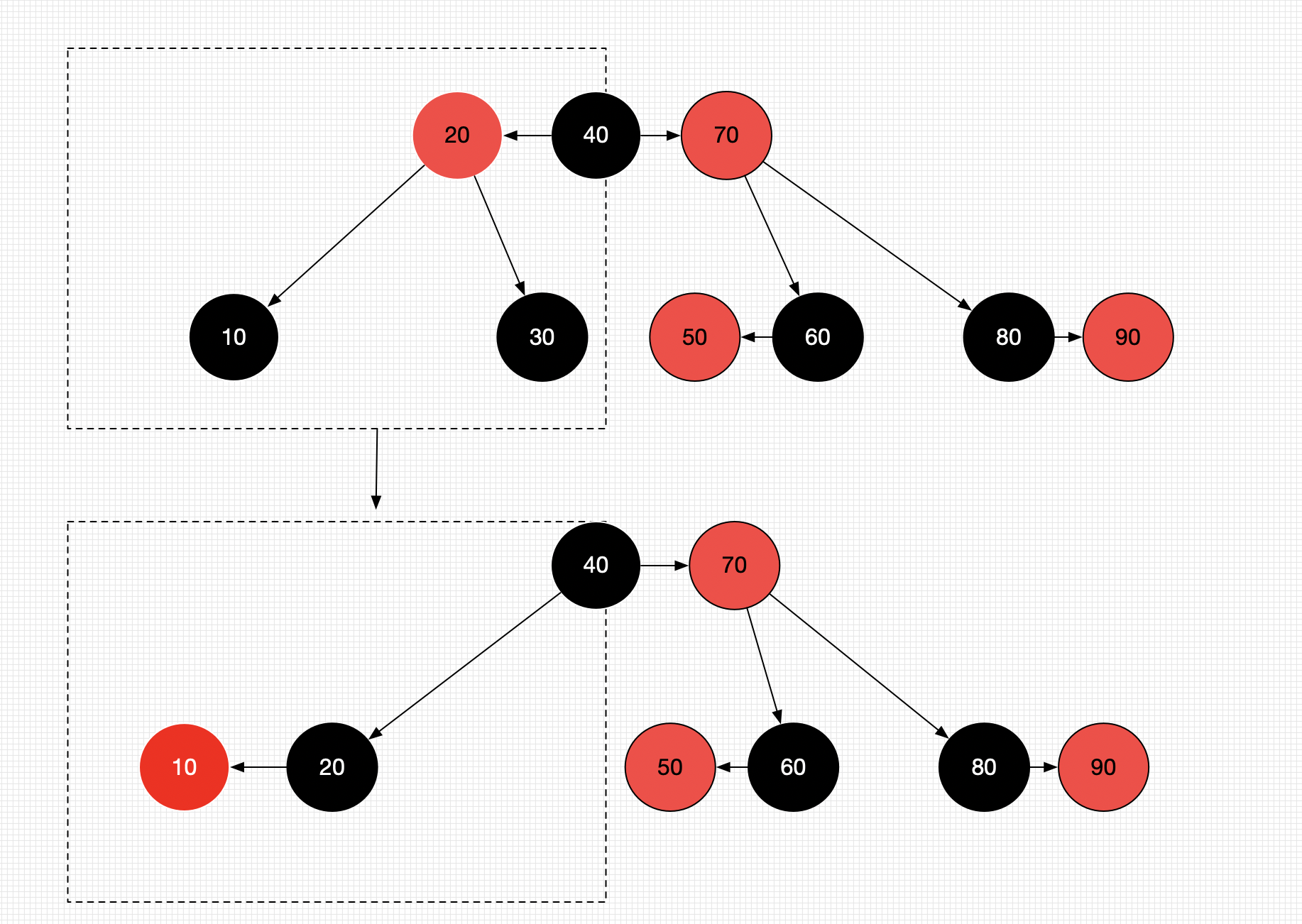
          • 删除情况2

    • 如果Black叶子节点的兄弟节点为Red

      • 原理： 此时兄弟节点是20 。 我们要将30变为45的兄弟节点。然后在进行兄弟节点为black操作

      • 将兄弟节点染成Black ,parent染成Red,再进行旋转。

      • 回到了兄弟节点为black的情况。

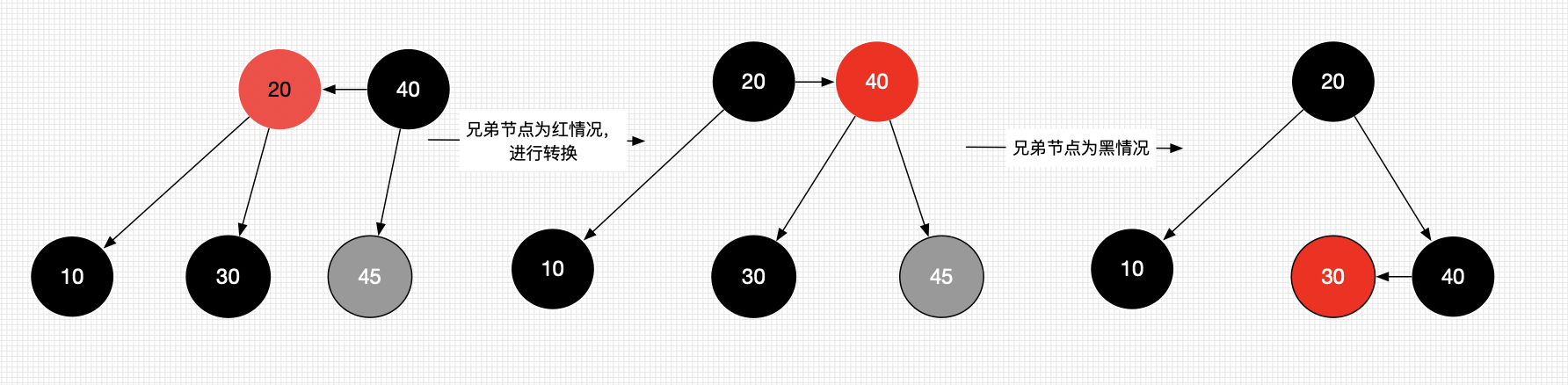
四、红黑树的平衡

红黑树是一种弱平衡。黑高度平衡，由于是黑高度平衡 和红黑树性质。所以最大路径小于最短路径的2倍

红黑树的最大高度是2 * log2^{n + 1}，依然是O(logn)级别。

五、时间复杂度

搜索：O(logn)

添加：O(logn)，O(1)次旋转操作

删除：O(logn)，O(1)次旋转操作

六、AVL树VS红黑树

  • AVL

    • 平衡标准比较严格：每个左右子树高度差1。

    • 最大高度是1.44 * log2^{(n + 2)} - 1.328(100W个节点，AVL最大高度28)。

    • 搜索、添加、删除都是O(logn)复杂度，其中添加需要O(1)次旋转调整、删除最多需要O(logn)次调整。

  • 红黑树

    • 平衡标准比较松：没有一条路径大于其他路径的二倍。

    • 最大高度是2 * log2^{(n + 1)}(100W个节点，红黑树最大高度40)。

    • 搜索、添加、删除都是O(logn)复杂度，其中添加删除都是O(1)次旋转调整。

  • 搜索的次数远大于插入和删除、选择AVL树；

  • 搜索、插入、删除的操作差不多，选择红黑树；

  • 相对于AVL，红黑树牺牲了部分平衡性能换取插入/删除时的少量旋转操作。整体性能优于AVL树

  • 红黑树的平均统计性能优于AVL树，实际应用更多选择红黑树。

喜欢的可以关注下我的公众号，会在第一时间更新

avatar
文章
阅读
粉丝