数据结构与算法(十一) B树

Rui4u君
823 阅读3分钟

B树

是一种平衡的多路搜索树，多用于文件系统、数据库的实现

  • 1个节点可以存储超过2个元素、可以拥有超过2个子节点
  • 拥有二叉搜索树的一些特质（小的子节点在左面 大的子节点在右面）
  • 平衡，每个节点的所有子树高度一致
  • 比较矮

m阶B树性质

一个节点最多拥有m个子节点

  • 假设一个节点存储元素个数为x
    • 根节点：1 \leq x \leq m-1
    • 非根节点：(ceiling(m/2) - 1) \leq x \leq = m-1
    • 如果有子节点 子节点个数为y = x + 1
  • 如果有子节点
    • 根节点上的子节点：2 \leq y \leq m
    • 非跟节点上的子节点：ceiling(m/2) \leq x \leq = m

celing为向上取整

  • 如果要是m = 3
    • 他的子节点个数为2 \leq y \leq 3，因此可称为（2，3）树、2-3树。
  • 如果要是m = 4
    • 他的子节点个数为2 \leq y \leq 4，因此可称为（2，4）树、2-3-4树。
  • 如果要是m = 5
    • 他的子节点个数为3 \leq y \leq 5，因此可称为（3，5）树、3-4-5树。

B树和二叉搜索树的关系

  • B树其实适合二叉搜索树是等价的
    • 只要把二叉搜索树和部分子节点与父节点结合就生成了b树
  • 多代节点合并，可以获得一个超级节点
    • 两代合并最多有4个子节点
  • m阶B树最多需要log{2^m}代合并

搜索

  • 1、现在节点内部从小到大搜索元素
  • 2、如果命中，搜索结束
  • 3、如果未命中，再去对应的子节点去搜索元素，重复步骤1

添加

元素必然是添加到叶子节点中

上溢

  • 假设3阶B树，当节点添加第三个数据的时候（最多添加两个） 叫上溢

假设B树的阶级为m， 上溢节点最中间的节点为k

  • 上溢的节点元素必然等于m
解决上溢
  • 将k位置的元素向上与父节点合并
  • 将[0,k - 1]和[k + 1,m - 1]位置的元素分裂成两个子节点
    • 这两个子节点的元素个数，必然都不会低于最低限制（ceiling(m/2) - 1）
  • 一次分裂完毕后，可能导致父节点上溢，重复上述方法
    • 最极端的情况是，一直上溢到根节点。
以4阶B树添加举例

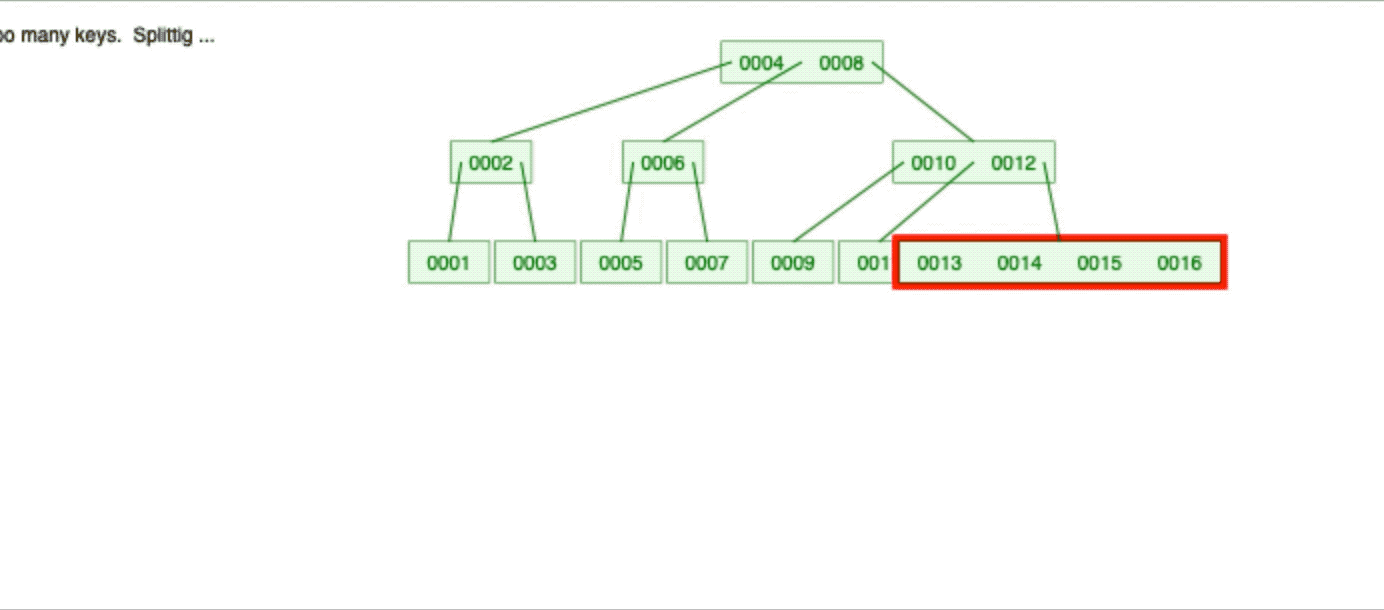
删除

叶子节点

​ 直接删除

非叶子节点

  • 找到前驱或者后继，覆盖删除所需要的元素的值。
  • 在把前驱或者后继删掉。
  • 非叶子节点的前驱或者后继必然在叶子节点中

下溢

  • 假设5阶B树，叶子节点最低个数为ceiling(m/2) - 1 = 2个 当删除后只剩下一个的时候 称为下溢
解决下溢：
  • 下溢的元素必然是ceiling(m/2) - 1 个
  • 如果下溢的节点的临近兄弟节点至少有(ceiling(m/2))个元素，可以向其借一个元素（最后一个元素）
    • 将父节点最后一个元素插入到下节点的最小位置
    • 将借来的元素插入到父节点最小位置
  • 如果下溢的节点的临近兄弟节点只有(ceiling(m/2)) - 1
    • 将父节点的中间元素挪下来与左右子节点进行合并
    • 合并后的节点元素等于ceil(m/2) + ceil(m/2) - 2; 不超过m - 1
      • 可能导致父节点下溢，下溢可能一直向上传播。（如果根节点下溢 就和子节点合并）
以4阶B树删除举例

​

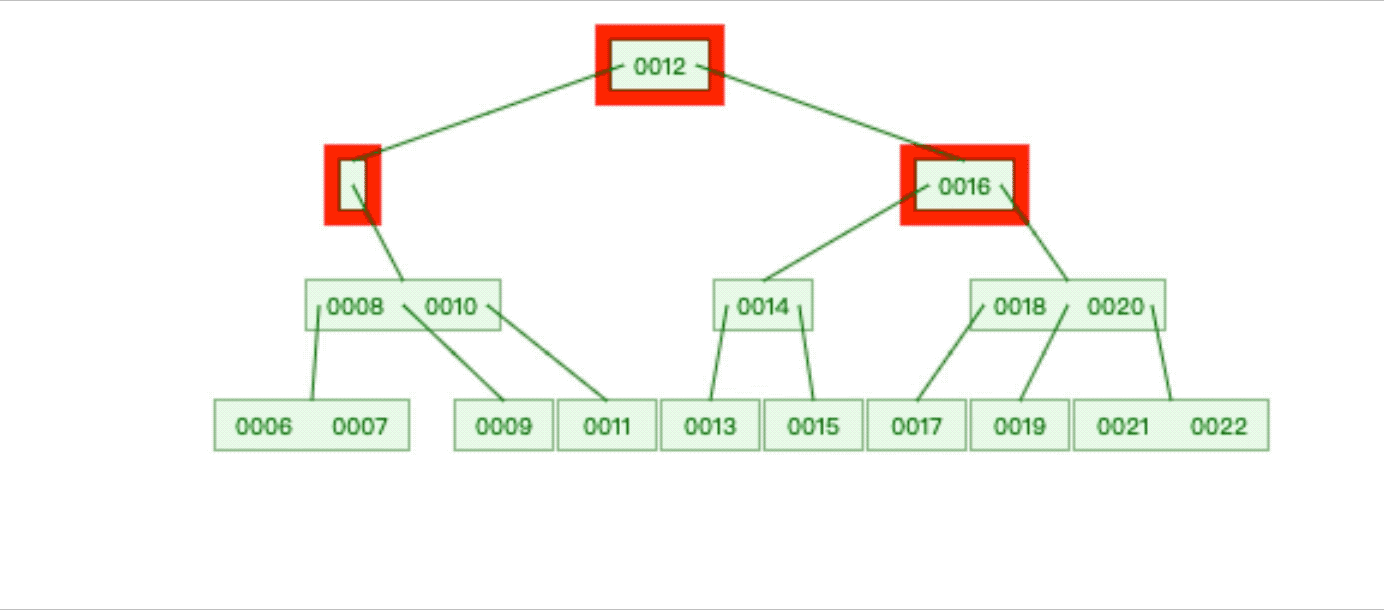
喜欢的可以关注下我的公众号，会在第一时间更新

avatar
文章
阅读
粉丝