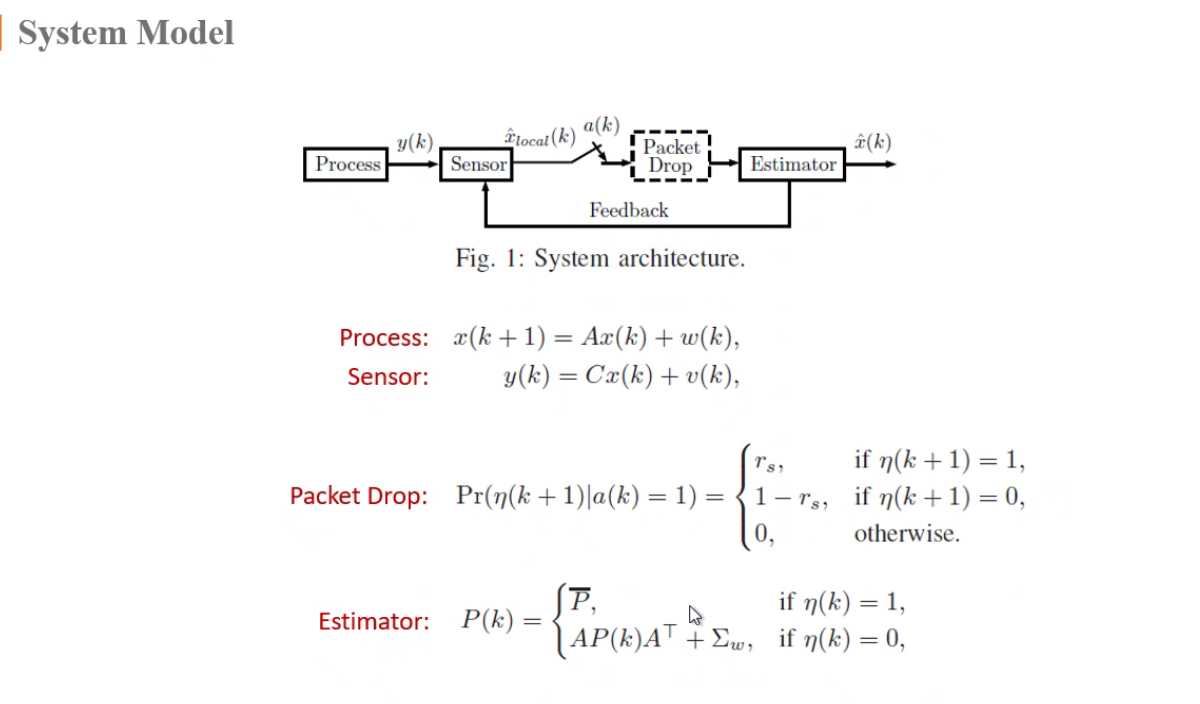
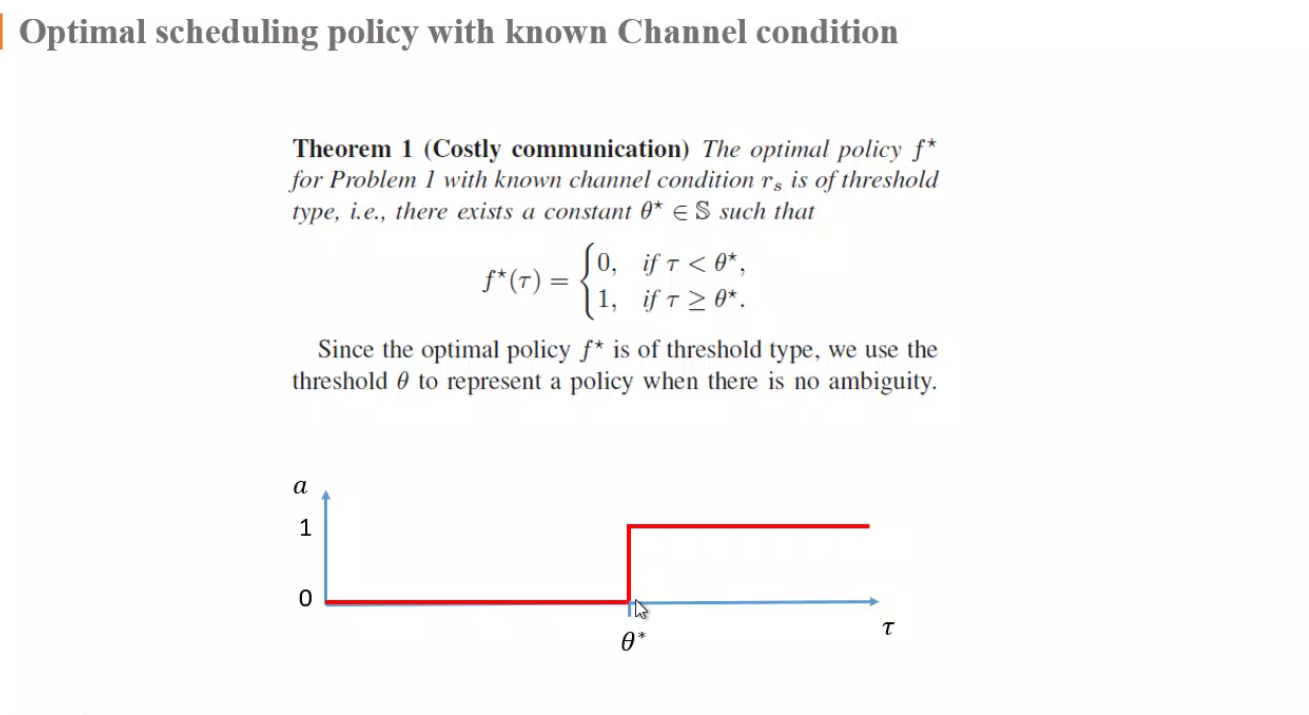
Learning Optimal Scheduling Policy for Remote State Estimation under Uncertain C

a(k)是策略

a=1发送，a=0不发送

$\tau$ 是状态

$\tau$ ：距离上一次接收到的时间

衡量指标

两个问题：

针对第一个问题，可以直接建立MDP模型

最下面的式子就是我们的目标函数(形式同问题一)

MDP解存在性引理，满足红框条件，就满足平稳策略=每一时刻的映射函数f是一样的

(3)是贝尔曼方程，j*是最小值，最优值

引理推出存在最优解，推出Q函数

解存在性引理由以下几个条件推导得出：

通过上述性质，就可以找到最优策略的结构

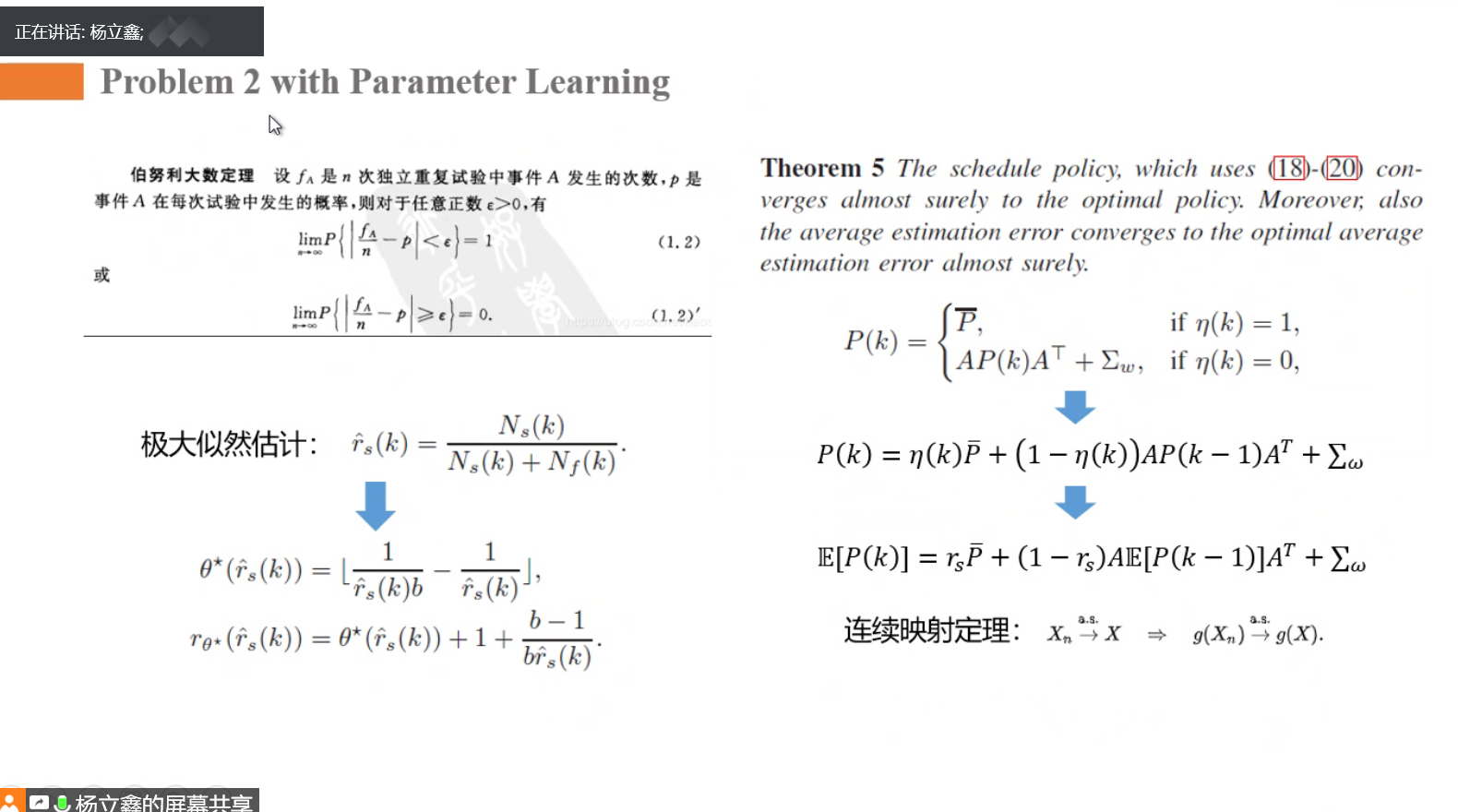
以下针对问题二：

讲代价函数分成两部分

☆ rs未知时，MDP的模型时未知的，用强化学习，如下：

两种方法：

随机逼近：Q-learning算法：

最优Q值是min

步长α=v_{k}依赖于被访问的次数

异步算法，每次只能访问一个动作对——》所以提出了改造方案：structural learning，通过之前证明的Q的次模性来改进，加快收敛速度

这里使用了梯度上升的方法

问题二

法一：

有约束条件的优化问题--用拉格朗日乘子法

λ用梯度上升的方法解，一直去迭代更新 $\lambda_{k+1}=\lambda_{k}+\beta(k)(a(n)-b)$

法二：