
画了N图后要关于实轴对称,形成封闭曲线

【结论】
对于最小相位系统: 从w=0往w=∞走路,视线内(-1,j0)在左手边则系统稳定,在右手边则系统不稳定
如:这个就稳定
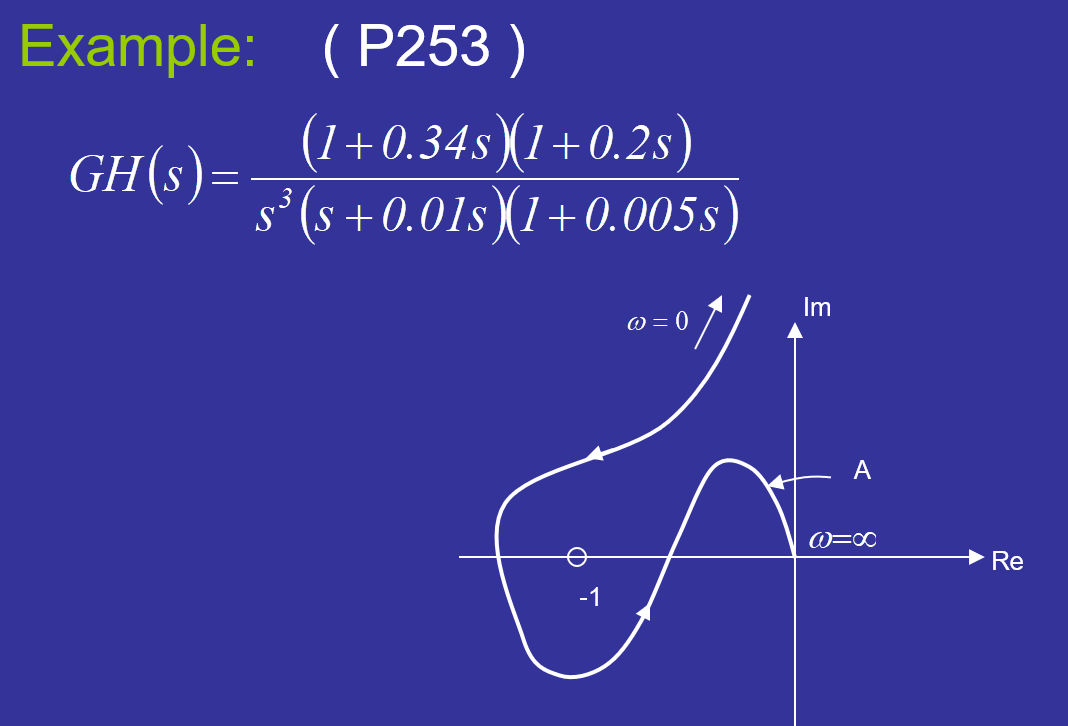
如果(-1,j0)外围了超多的线,判定转了多少圈:从(-1,j0)往外画一条射线(要交到所有线),看交点处是顺时针还是逆时针,则N=顺-逆
做题版:
STEP1: 绘制N图:

STEP2: 判断稳定性
①

经过(-1,j0)则临界稳定
或直接:N曲线不穿越(-1,j0)点,且绕着(-1,j0)点逆时针转P圈则系统稳定
special case:②对最小相位系统:系统稳定的充要条件是N曲线不包围(-1,j0)
如果控制系统开环传递函数的所有极点和零点均位于s左半平面上(包括虚轴),
则称该系统为最小相位系统。
因为最小相位系统极点都在左半平面,所以P=0,所以要想系统稳定即Z=0,则N必须=0即不包围(-1,j0)!
special case:
当系统的开环传函含有积分环节时,因为起点是从无穷远处过来,所以N曲线是非封闭曲线,故做辅助线半径为∞,角度为90*v的圆弧,再来判断N曲线包不包围(-1,j0)
王老师
柰氏图稳定判据
