高级 DP
高级 DP, 顾名思义,是比较复杂的 DP 问题,这种复杂主要体现在三个方面
- 状态有更多维度,二维、三维或者更多,甚至需要压缩
- dp 方程更加复杂
- Corner Cases 更多,容易漏
这就需要我们更多的练习,提高编程基本功、逻辑思维能力、数学能力,以练就看到问题就能准确又快速地定义且推导出正确的 DP 状态方程。话不多说,下面给出几道高级 DP 问题,大家可以体验一下这个难度,还有 DP 方程的推导。
经典例题
32.最长有效括号
思路:
- 暴力,栈,双重遍历子序列,看是否有效,
O(n^3) - 栈,一次遍历,贪心,找到一对括号才更新最大长度,
O(n^2) - 高级DP
- s[i] == ')' 且 s[i-1] == '(',形如".....()",
dp[i] = dp[i-2] + 2 - s[i] == ')' 且 s[i-1] == ')',形如".....))",此时如果s[i - dp[i-1] - 1] == '(',有
dp[i] = dp[i - dp[i-1] - 2] + dp[i-1] + 2
- s[i] == ')' 且 s[i-1] == '(',形如".....()",
高级DP
class Solution {
public int longestValidParentheses(String s) {
int[] dp = new int[s.length()];
int res = 0;
for (int i = 1; i < s.length(); ++i) {
if (s.charAt(i) == ')') {
if (s.charAt(i - 1) == '(') {
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
dp[i] = dp[i - 1] + (i - dp[i - 1] >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
818.赛车
思路:
- BFS,时间
O(target * log(target))空间O(target * log(target)) - DP,时间
O(target * (log(target))^2)空间O(target)- AAA...RAAA...R,车还没开到,currPos < target,正向加速 acc_cnt,反向加速 rev_acc_cnt,
dp[i] = min(dp[i], acc_cnt + 1 + rev_acc_cnt + 1 + dp[i - (currPos - revPos)] - AAAA, 只用加速刚好到 target
dp[i] = min(dp[i], acc_cnt) - AAA...RAAA... 车开过了,currPos > target,
dp[i] = min(dp[i], 1 + acc_cnt + dp[currPos - 1]
- AAA...RAAA...R,车还没开到,currPos < target,正向加速 acc_cnt,反向加速 rev_acc_cnt,
class Solution {
public int racecar(int target) {
int[] dp = new int[target + 1];
for (int i = 1; i <= target; ++i) {
dp[i] = Integer.MAX_VALUE;
int acc_cnt = 1, currPos = 1;
// AAA...RAAA...R
while (currPos < i) {
for (int rev_acc_cnt = 0, revPos = 0; revPos < currPos; revPos = (1 << ++rev_acc_cnt) - 1) {
dp[i] = Math.min(dp[i], acc_cnt + 1 + rev_acc_cnt + 1 + dp[i - (currPos - revPos)]);
}
currPos = (1 << ++acc_cnt) - 1;
}
// AAAA or AAA...RAAA...
dp[i] = Math.min(dp[i], acc_cnt + (currPos == i ? 0 : 1 + dp[currPos - i]));
}
return dp[target];
}
}
字符串算法
字符串问题,是最接近我们实际工作的一类问题,另一类问题是排序,因此在笔试面试中非常常见。这里对字符串问题做一个全面汇总,让大家以后遇到此类问题能心中不慌。首先,字符串问题可以分为以下几类:
- 字符串基础
- 字符串操作
- 异位词问题
- 回文串问题
- 最长子串、子序列问题
- 字符串匹配问题
其次,我会带着大家过一遍,每类问题我都会给出一些基本认识和经典例题。
字符串基础
在 Java、JS、Python 里,String 是 Immutable (不可变) 的,意思是无法修改字符串某个索引的字符,只能复制新的字符串,或者说,只能浅拷贝。但是否所有编程语言中的字符串都是不可变的呢?其实不是,像下面几种语言的 String 就是 mutable 的:
- Ruby
- PHP
- C++ 、 C(其实没有 String 类,用
char *表示) - Swift
387.字符串第一个唯一字符
JS
// 哈希
var firstUniqChar = function(s) {
let map = {}
for (const char of s) {
map[char] = ++map[char] || 0
}
for (let i = 0; i < s.length; ++i) {
if (map[s[i]] == 0) return i
}
return -1
};
// 骚操作
var firstUniqChar = function(s) {
for (const char of s) {
if (s.indexOf(char) == s.lastIndexOf(char))
return s.indexOf(char)
}
return -1
};
Java
class Solution {
public int firstUniqChar(String s) {
Map<Character, Integer> map = new HashMap<>();
for (char c : s.toCharArray()) {
map.put(c, map.getOrDefault(c, 0) + 1);
}
for (int i = 0; i < s.length(); ++i) {
if (map.get(s.charAt(i)) == 1)
return i;
}
return -1;
}
}
字符串操作
反转字符串相关的操作熟悉一下,也是基础。
557.反转字符串中的单词 III ✨
这道题是腾讯的面试题,大家感受一下。
class Solution {
public String reverseWords(String s) {
char[] a = s.toCharArray();
int i = 0, j = 0;
while (j < a.length) {
while (j < a.length && a[j] != ' ') j++;
reverse(a, i, j - 1);
i = j + 1;
j++;
}
return String.valueOf(a);
}
private void reverse(char[] a, int start, int end) {
while (start < end) {
char tmp = a[start];
a[start++] = a[end];
a[end--] = tmp;
}
}
}
异位词问题
高频题目,最好把各种解法都掌握。
438.找到字符串中的所有异位词
思路:
- 暴力,遍历 s,将 s 的子串与 t 比较是否互为异位词,时间复杂度
O(mn) - 滑动窗口,复杂度
O(m),也是最优解
暴力
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> res = new ArrayList<>();
int m = s.length(), n = p.length();
if (m < n) return res;
for (int i = n; i <= m; ++i) {
if (isAnagram(s.substring(i - n, i), p)) {
res.add(i - n);
}
}
return res;
}
private boolean isAnagram(String s, String p) {
int[] cnt = new int[26];
for (int i = 0; i < s.length(); ++i) {
cnt[s.charAt(i) - 'a']++;
cnt[p.charAt(i) - 'a']--;
}
for (int n : cnt) {
if (n != 0) return false;
}
return true;
}
}
滑动窗口
class Solution {
public List<Integer> findAnagrams(String s, String p) {
List<Integer> res = new ArrayList<>();
Map<Character, Integer> need = new HashMap<>();
Map<Character, Integer> window = new HashMap<>();
int left = 0, right = 0;
int validCnt = 0;
for (char c : p.toCharArray()) need.put(c, need.getOrDefault(c, 0) + 1); // 初始化要求
while (right < s.length()) {
char rChar = s.charAt(right++); // 窗口右滑
if (need.containsKey(rChar)) {
window.put(rChar, window.getOrDefault(rChar, 0) + 1);
if (window.get(rChar) <= need.get(rChar)) validCnt++; // <= 为了处理重复字符如"baa""aa"的cases
}
while (validCnt == p.length()) {
if (right - left == p.length()) res.add(left); // 满足某种条件时更新 res
char lChar = s.charAt(left++); // 窗口左滑
if (need.containsKey(lChar)) {
window.put(lChar, window.get(lChar) - 1);
if (window.get(lChar) < need.get(lChar)) validCnt--; // 窗口不满足要求
}
}
}
return res;
}
}
回文串问题
有点 tricky 的一类问题,重点是如何更好地利用回文串的性质。
680.验证回文字符串 II
思路:
- 暴力,删掉某个字符,看剩下的是否回文
O(n^2) - 贪心,如果首位字符不同,那么只用判断
(i+1, j)(i, j- 1)是否回文(删首或者尾)
class Solution {
public boolean validPalindrome(String s) {
char[] a = s.toCharArray();
for (int i = 0, j = a.length - 1; i < j; ++i, --j) {
if (a[i] != a[j]) {
return isPalindrome(a, i + 1, j) || isPalindrome(a, i, j - 1);
}
}
return true;
}
private boolean isPalindrome(char[] a, int i, int j) {
while (i < j) {
if (a[i++] != a[j--]) return false;
}
return true;
}
}
最长子串、子序列问题
高频,通用解法一般是 DP。
1143.最长公共子序列 LCS ✨
思路:
- 暴力
- DP
a. 分治
LCS[i] = max(最后一个字母相同,最后一个字母不相同)b. 状态定义f[i][j]c. DP方程if text1[-1] == text2[-1]: dp[i][j] = dp[i-1][j-1] + 1 else: dp[i][j] = max(dp[i-1][j], dp[i][j-1])
DP-Java
class Solution {
public int longestCommonSubsequence(String text1, String text2) {
int m = text1.length();
int n = text2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
5.最长回文子串
思路:
- 暴力
O(n^3) - DP 空间 + 时间复杂度
O(n^2) + O(n) - 从中间向外扩散
O(n^2) + O(1)
DP
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
boolean[][] dp = new boolean[n][n];
String res = "";
for (int i = n - 1; i >= 0; --i) {
for (int j = i; j < n; ++j) {
dp[i][j] = s.charAt(i) == s.charAt(j) && (j - i < 2 || dp[i + 1][j - 1]);
if (dp[i][j] && (j - i + 1) > res.length()) {
res = s.substring(i, j + 1);
}
}
}
return res;
}
}
中间向外扩散
class Solution {
private int lo, maxLen;
public String longestPalindrome(String s) {
if (s.length() < 2) return s;
for (int i = 0; i < s.length(); ++i) {
extendPalindrome(s, i, i); // odd
extendPalindrome(s, i, i + 1); // even
}
return s.substring(lo, lo + maxLen);
}
private void extendPalindrome(String s, int j, int k) {
while (j >= 0 && k < s.length() && s.charAt(j) == s.charAt(k)) {
j--;
k++;
}
if (k - j - 1 > maxLen) {
lo = j + 1;
maxLen = k - j - 1;
}
}
}
字符串匹配问题
此类问题一般是给你两个字符串,问你是否匹配、或增加删除修改某个字符后是否能匹配。通常来讲,解法都是动态规划。
72.编辑距离 ✨
思路:
- 双端 BFS
- DP,我们可以用
dp[i][j]来表示 word1 的前 i 个字符与 word2 的前 j 个字符的编辑距离,我们可以像下面这样画个表格来辅助理解
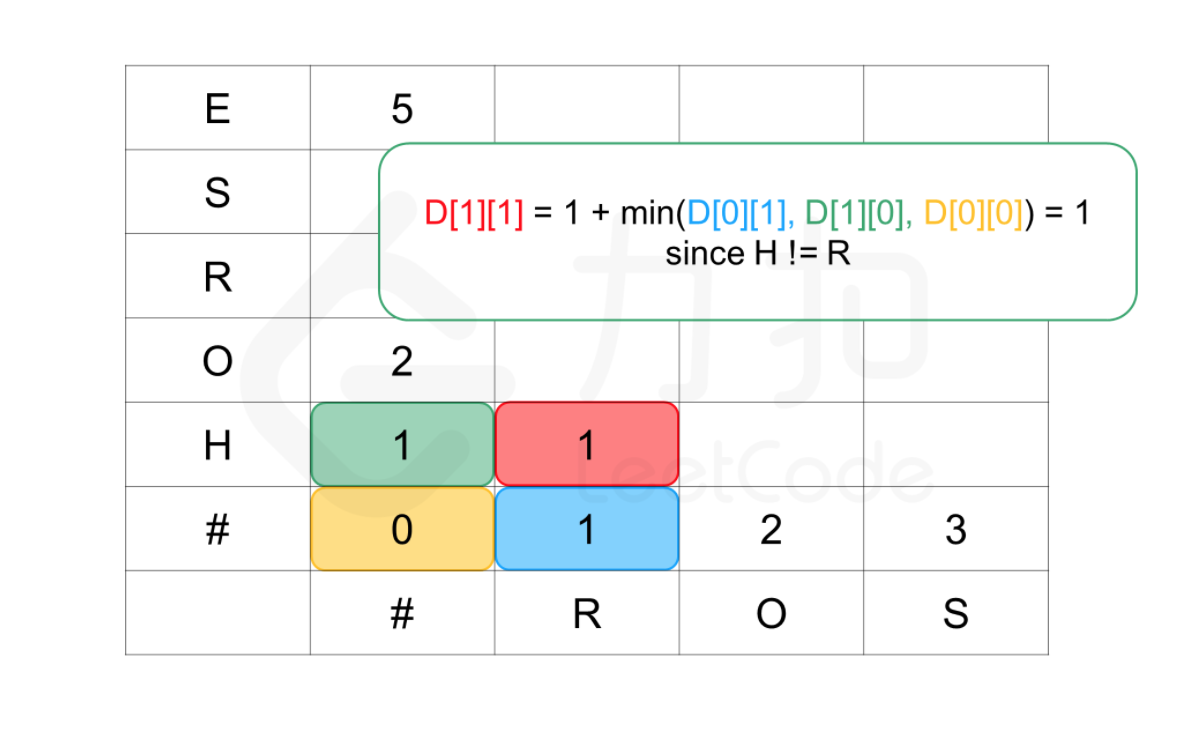
这里给出 DP 方程
if word[i] == word[j]:
dp[i][j] = dp[i - 1][j - 1]
else:
dp[i][j] = min(dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]) + 1
Java 题解
class Solution {
public int minDistance(String word1, String word2) {
int m = word1.length();
int n = word2.length();
int[][] dp = new int[m + 1][n + 1];
for (int i = 0; i <= m; ++i) dp[i][0] = i;
for (int j = 0; j <= n; ++j) dp[0][j] = j;
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (word1.charAt(i - 1) == word2.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1];
}else {
dp[i][j] = Math.min(Math.min(dp[i - 1][j], dp[i][j - 1]), dp[i - 1][j - 1]) + 1;
}
}
}
return dp[m][n];
}
}
10.正则表达式匹配
思路:
- 高级DP,
dp[i][j]: S 的前 i 个字符是否能被 P 的前 j 个字符匹配
class Solution {
public boolean isMatch(String s, String p) {
int m = s.length();
int n = p.length();
boolean[][] dp = new boolean[m + 1][n + 1];
dp[0][0] = true;
// s: '', p: '#*#*#*#*#*'
for (int j = 2; j <= n; j += 2) {
if (p.charAt(j - 1) == '*' && dp[0][j - 2]) {
dp[0][j] = true;
}
}
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
// s: '####a', p: '####.'
if (s.charAt(i - 1) == p.charAt(j - 1) || p.charAt(j - 1) == '.') {
dp[i][j] = dp[i - 1][j - 1];
// s: '#####a', p: '####a*'
} else if (p.charAt(j - 1) == '*') {
// s: '#####b', p: '####a*'
if (p.charAt(j - 2) != '.' && s.charAt(i - 1) != p.charAt(j - 2)) {
dp[i][j] = dp[i][j - 2]; // '*' as empty
} else {
// '*' as 0, 1, multiple
dp[i][j] = dp[i][j - 2] || dp[i - 1][j - 1] || dp[i - 1][j];
}
}
}
}
return dp[m][n];
}
}
对于此类问题大家可能拿到之后感觉难以下手,别慌,我自己总结了字符串匹配类问题的模板,分享给大家。
字符串匹配问题模板
public <T> StringDP(String A, String B) {
// 1. initializing
int m = A.length();
int n = B.length();
<T>[][] dp = new <T>[m + 1][n + 1];
dp[0][0] = INIT_VALUE;
for (int i = 1; j <= m; ++i) {
Initialize(dp[i][0]);
}
for (int j = 1; j <= n; ++j) {
Initialize(dp[0][j]);
}
// 2. Iterating
for (int i = 1; i <= m; ++i) {
for (int j = 1; j <= n; ++j) {
if (Condition_1) {
Update(dp[i][j]);
} else if (Condition_2) {
if (SubCondition_1) Update(dp[i][j]);
else Update(dp[i][j]);
}
...
}
}
// 3. Result
return dp[m][n];
}