九、on-policy prediction with approximation
“这种思想的主要任务就是求该函数的参数”,如何求?分为以下三个步骤:
(1)确定价值函数的拟合模型
(2)确定待优化的目标函数
(3)确定参数的更新算法
9.1.确定价值函数的拟合模型:
1.1 价值函数的参数方程表示 v(s,w)
1.2 确定训练样本 s → u的实际样本
1.3 拟合模型的选择
模型需要满足RL特有的两个条件:
① 强化学习任务需要实时在线学习,一边和环境交互一边学习。因此需要一个效率很高的模型,可以不断接收新增的训练样本进行快速学习。
② 强化学习任务需要处理”非稳态目标函数”问题。 ------有个迭代的变化过程
(GPI中pi一变qpi就会跟着变。bootstrapping中valve值也是也是一直在变化的)
9.2 确定待优化的目标函数:
2.1 为什么建立目标函数:目标函数=损失函数。确保模型越来越好。
区别于表格方法,①因为表格方法的值通过不断迭代最终是可以自动收敛的
②表格方法中各个状态的值更新过程没啥关系:A value更新后不影响B C的value。而函数近似方法:A value变化后,模型参数w就会变化,影响到所有状态更新。
我们的状态都有权重,一个状态准确一点,其他状态就会不准确一点,所以我们需要重点关注我们关心的状态,所以我们需要知道状态分布μ(s)
2.2 确定目标函数
VE(w)
miu 的数学含义:通常 miu 表示在目标策略 pi 下,花在状态s上的时间占总时间的比例
2.3 求解目标函数
全局最优解---线性容易,非线性(神经网络)难----局部最优解
3 确定参数w的更新算法(找到一个w* 使得 VE(w)全局或局部最优)

BGD批量梯度方法:每次迭代用所有的数据对参数进行更新(用期望)
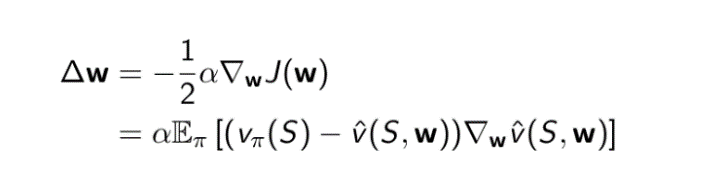
=α∑[..-..]/M
BUT无法实现,无法得到所有状态真实值(或Ut值),所以使用SGD随机梯度方法,选择一个样本一个真实值(或Ut值)来更新参数w:
随机梯度方法《----朝着ve(w)下降最快的方向更新W,必须small step 更新,不能沿着这个方向彻底完全更新《----随机梯度下降理论(SGD)
reason:①为了保证收敛到局部最优---必须满足随机逼近理论-----α随着时间减少-----》所以α不能太大,以至于一下子更新太多
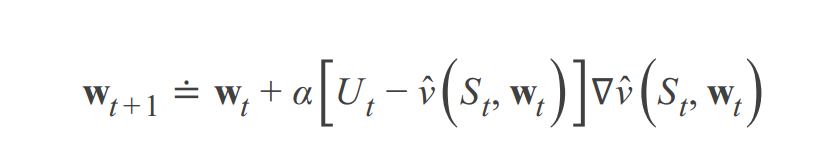
有可能训练样本得出的不是准确的vΠ(st)值,所以Ut是样本的估计值

第二个条件=α随着时间减少
半梯度法与普通的梯度下降形式一致,区别仅在于 target 的选取,即训练样本的 output 是否是 input 的无偏估计---- MC是梯度,TD(0)、TD(λ)、DP是半梯度
半梯度法虽然收敛性不如真正的梯度下降法,但他有如下优点:
1. 半梯度法在线性模型下仍能确保收敛。
2. 在可收敛的前提下,半梯度法收敛速度很快。
3. 半梯度法可用于连续型任务,无需等待一个完整的 episode 结束。 (DP,TD)
9.4 Linear Methods
用一组表示状态St的特征值向量X(St)来去得到我们的逼近值V(S,W)
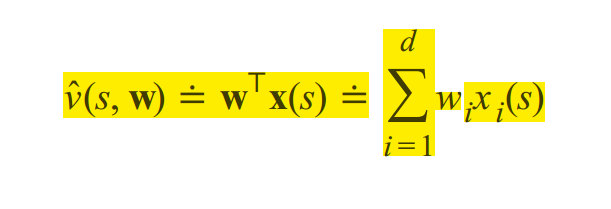
带入到J(w)损失函数中,求J(w)的梯度,更新W:
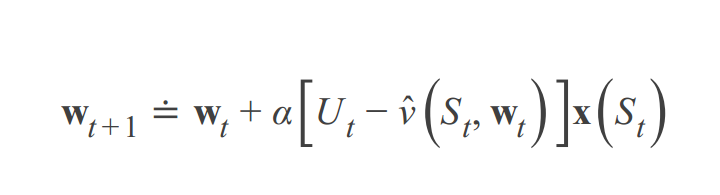
线性方法优点:对于大部分方法MC、TD,都可以收敛,而且实际运用也很有效
线性形式的限制:是它不能考虑特征之间的任何相互作用
9.5 对于线性方法如何构建特征函数
多项式、傅里叶、coarse coding 、Tile Coding、RBF
9.6 用神经网络构建非线性的函数近似
9.7最小二乘TD方法 LSTD
WHAT: TD半梯度更新公式,通过boostrapping会收敛到一个W*,使得VE最小,这个W*叫做TD不动点,然后现在我们不进行boostrapping,每一步直接另Wt+1=Wt+B中的B项为零,解出这个时间步下的TD不动点
WHY:①虽然LSTD 比普通的迭代法的计算量更大,但是他的优势在于对数据的利用效率更高。???
③ 此外,LSTD 无需设置步长参数α,取而代之地是只需设置一个较小的ε即可,省去了调参的环节。但是没有步长,意味着这个算法缺乏『遗忘性』 ?
9.8基于内存的函数近似
WHAT:不通过建立一个含参数的近似函数来计算值,而是把遇到的每个状态都记录下来!!那不就是等同于表格方法吗???
WHY:①可以避免维数灾难???
① 轨迹采样,可以关注需要的状态
9.10 Kernel-based Function Approximation 基于核(distance)的函数近似
核 = 权重 = 距离
函数逼近:
Gradient Q-learning不能适用再non-linear的函数逼近(神经网络)。
它没有充分利用sample(sample efficient)
所以我们引出最小二乘法,
实现方法和结果不同:最小二乘法是直接对🔺求导找出全局最小,是非迭代法。而梯度下降法是一种迭代法,先给定一个β,然后向🔺下降最快的方向调整β,在若干次迭代之后找到局部最小。梯度下降法的缺点是到最小点的时候收敛速度变慢,并且对初始点的选择极为敏感,其改进大多是在这两方面下功夫。
Summary:
在无限状态空间mdp问题上,表格RL方法不再适用,我们需要一种泛化的方法来解决这种问题。
泛化---》监督学习-à将获得的样本作为训练样本,其值为Ut。Ut可用MC、TD(入)、TD(0),来得出。
一种方法是参数化函数近似,包含一个权重参数W,通过线性估计(特征向量)或者非线性估计(network)估计出V`。然后和训练样本的估计值做MSVE得到VE,通过随机梯度下降,不断地使VE减小,更新W值,直到收敛,得到W*,即得到最优的近似函数。
注:线性估计中的特征向量可以用多项式、傅里叶基、粗编码、径向基函数 (效果越来越好)
VE可以使用LSTD法(最小二乘法)----具有data efficiency.