矢量 -- 图形の万恶之源意思为可缩放的矢量图形。但它的概念不止于此。它还有一个叫法：向量。说到这玩意，大家瞬间想

说到矢量，很多人第一反应是 SVG，
SVG 的全称是 Scalable Vector Graphics，

意思为可缩放的矢量图形。
Vector 确实是 SVG 中重要的一部分，
但它的概念不止于此。

向量

Vector -- 矢量
它还有一个叫法：向量。

说到这玩意，大家瞬间想起了被高数支配的恐惧。
没错，它可以说是线性代数中老大哥的存在。

wiki 上有关于线性代数的详细介绍：

很多相关资料会把线性代数和计算机图形学联系起来，
它们之间究竟有什么关系呢？

点

二维的原点 (0,0)
三维的原点 (0,0,0)

向量

把点与原点连接起来就形成向量，
向量代表一个有方向的长度，
对应标量。

元向量

元向量表示 X 或 Y 轴上一个单位的向量，
两个元向量任意组合可以表达二维面上的任何一个坐标，
~~每个向量也都可以拆分成多个元向量的分量。~~

线 & 面

把线和面放在同个 tab 是因为这两个东西的抽象意义是一致的。
它们表示一定条件下的元素合集，
在线性代数中我们称之为向量空间
wiki 上有关于向量空间的详细介绍：

矩阵

A=
\left[
\begin{matrix}
2 \\
2 \\
\end{matrix}
\right]

这个矩阵表示是什么意思呢？
它表示的是一个由两个元向量组成的向量，
它在 X 和 Y 分别有 (2, 2) 两个标量的分量。

矩阵相乘

2 维

这里有两个矩阵：

A=
\left[
\begin{matrix}
3 \\
2 \\
\end{matrix}
\right]

B=
\left[
\begin{matrix}
2 & 3 \\
2 & 4 \\
\end{matrix}
\right]

A * B 代表什么呢？
我们先画一个坐标系：

A 可以理解为 (2, 2) 标量的两个 [X Y] 元向量之和。
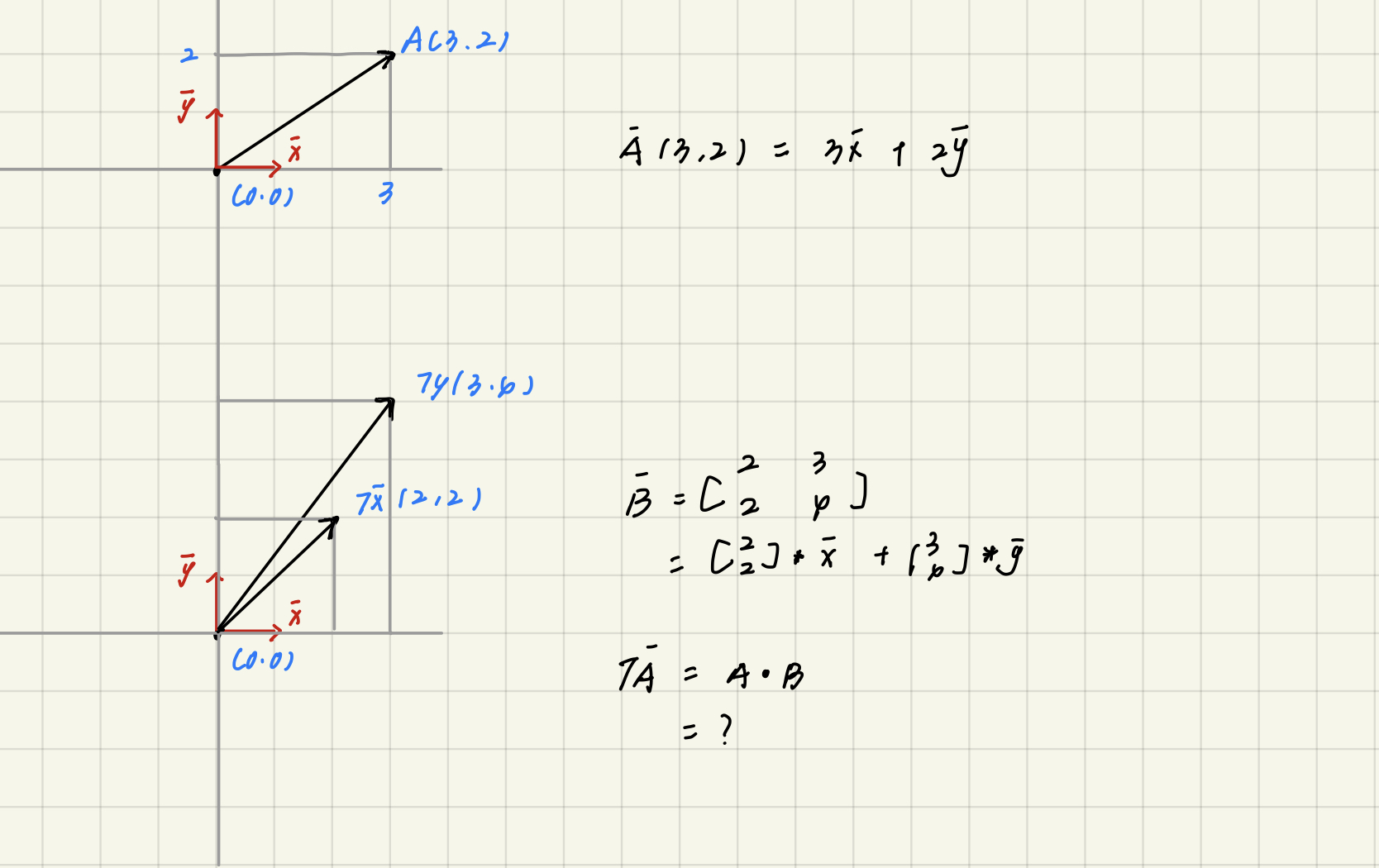
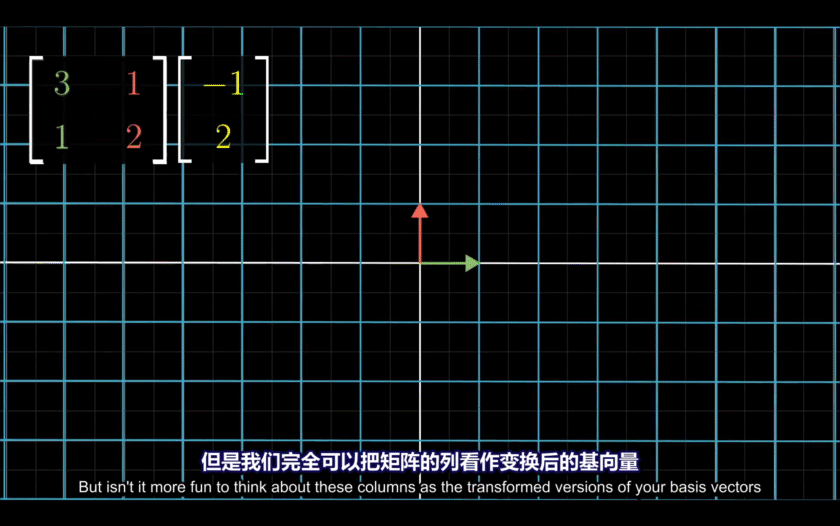
B 可以理解为两个分量分别作用于 X Y 两个元向量。

Tx = X*
\left[
\begin{matrix}
2 \\
2 \\
\end{matrix}
\right]

Ty = Y*
\left[
\begin{matrix}
3 \\
4 \\
\end{matrix}
\right]

A * B 可以理解为，
B 作用于坐标系的元向量产生一个新的坐标系，
A 在新的坐标系中的表现。

3 维

矩阵的大部分性质与维度无关，
之前我们基于二维世界理解的矩阵，
放在三维世界中同样适用。

举个旋转的栗子：

T =
\left[
\begin{matrix}
0 & 0 & 1 \\
0 & 1 & 0 \\
-1 & 0 & 0 \\
\end{matrix}
\right]

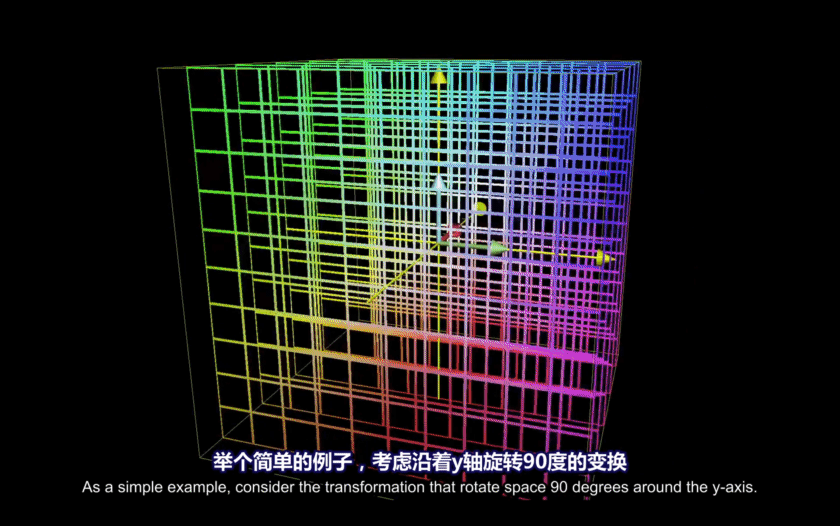
很眼熟有木有，
恭喜你理解了 Transform-3D 原理，
而这部分知识，在线性代数中称之为线性变换。

矢量图型

矢量在图形渲染中也大有用途。

元数据 & 帧数据

由于屏幕物理结构限制，
绝大部分现代计算机显示器都要将数据转换成栅格图像才能显示，

用于计算的数据叫元数据，
计算得出的栅格图像叫帧数据。

比起帧数据，矢量元数据使用更少的信息，
保存更多的参数用于目的帧渲染。

wiki 上有关于矢量图形的详细介绍：

点

线

Path

如果用文本编辑器打开 SVG 文件(XML),
你会发现 SVG 中有一段:

M153 334 
C153 334 151 334 151 334 
C151 339 153 344 156 344 
C164 344 171 339 171 334 
C171 322 164 314 156 314 
C142 314 131 322 131 334 
C131 350 142 364 156 364 
C175 364 191 350 191 334 
C191 311 175 294 156 294 
C131 294 111 311 111 334 
C111 361 131 384 156 384 
C186 384 211 361 211 334 
C211 300 186 274 156 274

Paint.stroke

Stroke

Paint.fill

Fill

TrimPath

面

矩形

圆形

椭圆

多边形

矢量动效

结合上面讲的 Transform 和矢量属性效果，
我们可以完成计算机中几乎所有的图形绘制。

以下通过几个常见动效，介绍动效的制作步骤：

React LOGO

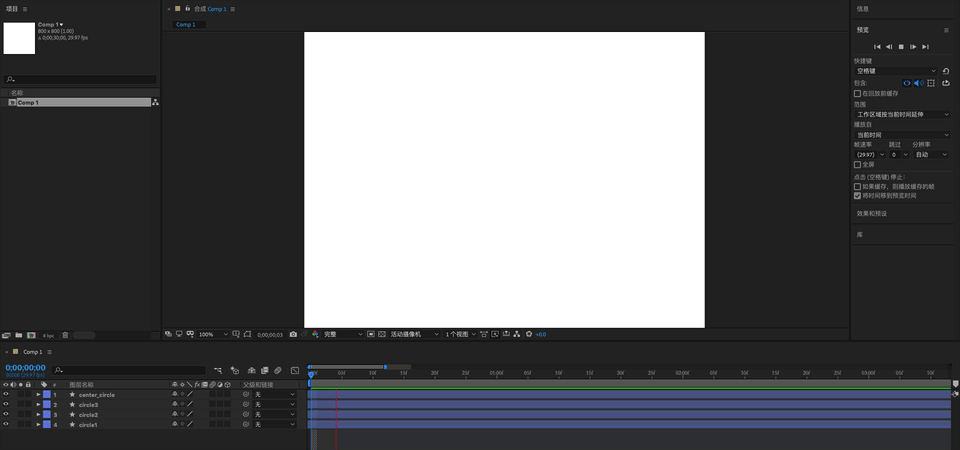
React LOGO 可以拆分成四个部分，
里面一个 Circle fill 的 Scale 动画
外面三个环绕 Circle stroke path 并添加 Trim & Width 动画

通过 SVGA Preview 我们可以清晰了解它的结构：

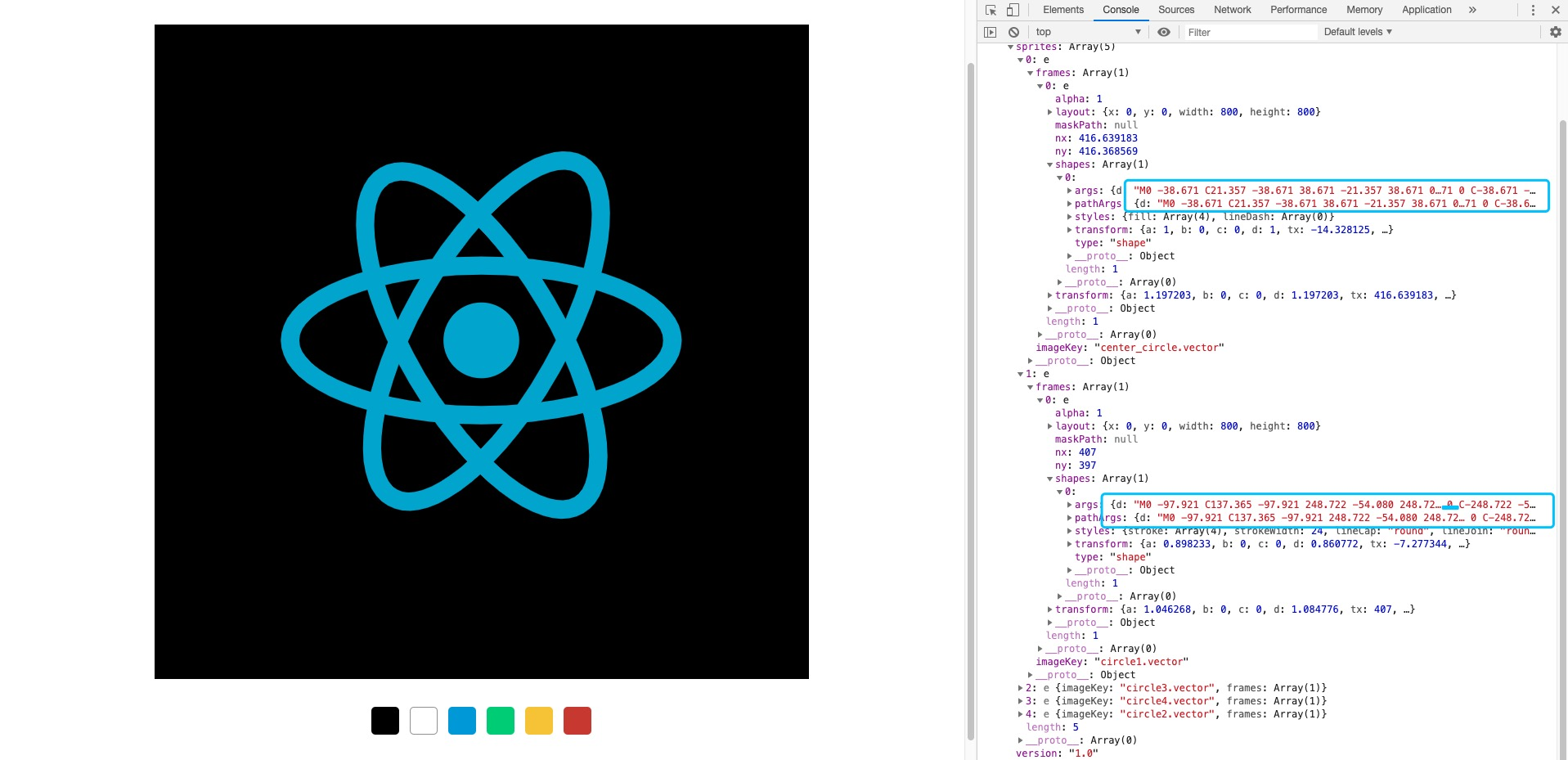
React LOGO 只使用矢量图形属性动画。

Star moving

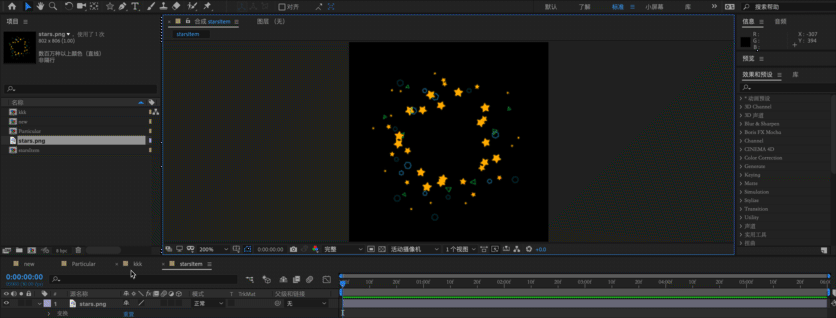
Star moving 可以拆分成两个部分：
使用矢量形状绘制大小颜色不一的星星形状
给星星逐个应用 Transform 动效向外位移。

矢量 -- 图形の万恶之源

向量

点

向量

元向量