注:标记书中页码对应《RL:An introduction》
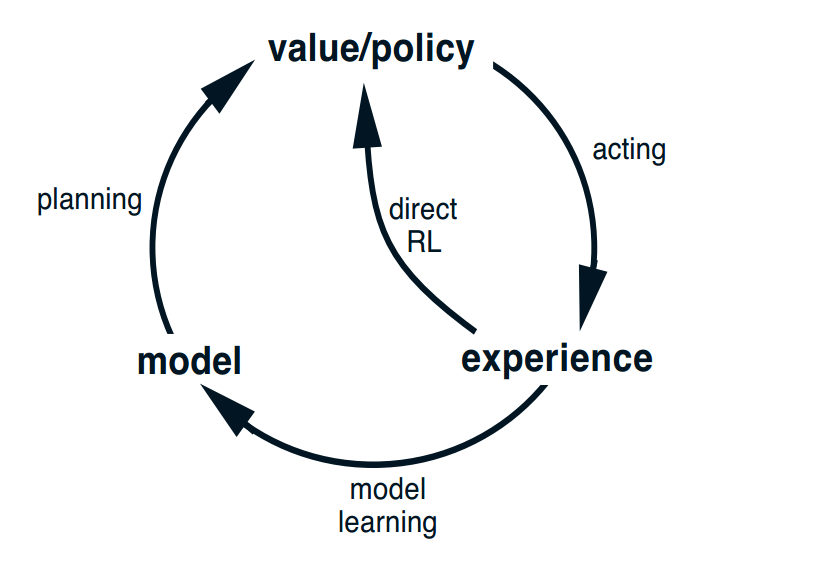
在这章中,我们将要介绍如何将“learning”与“planning”结合起来,利用二者的优点得到一个更好的算法。并且介绍一下许多关于planning的重要内容。
根据这个图,我们先来介绍一下什么是learning、planning、model和model learning。
首先我们根据初始化的值或者策略,和环境交互(就是这里的acting),然后通过direct RL方法去估计值函数和改进策略,这就是我们前面两章蒙特卡洛和时间差分算法的内容。
在强化学习中model指的是agent可以对预测环境如何的去反应它的操作,它分为分布模型和样本模型,。分布模型就是知道了所有结果的可能性及其概率,也就是我们之前说的它知道了状态转移概率P和获得的reward。而样本模型指的是只产生一种可能性,根据概率进行采样,就和蒙特卡洛方法一样,和环境进行交互获得一条可能的路径,也就是模拟的经验。分布模型比样本模型更强大,知道分布模型就可以用动态规划的方法直接解决问题,但是在现实的应用中,获取样本模型比分布模型容易得多。
Model learning就是从实际经验中学习和改进model。Planning过程包括了用model生成模拟经验,然后我们将强化学习的方法直接应用在模拟经验中,用以改进我们的value和policy。也就是说,我们的learning和planning的唯一区别就是他们的经验来源,一个是真实的经验,另一个是通过model生成的模拟的经验。

Dyna-Q算法就是一个整合了learning和planning的方法,这是他的伪代码。165页的图片也可以看出,Dyna-Q方法的效果远远好于单纯的learning方法。
接下来讲的几节都是基于对planning的改进,我就通过Dyna-Q这个框架介绍一下,然后最后详细讲这一章最重要的内容蒙特卡洛树搜索。
8.3节中。因为我们的model是通过真实经验学习到的,环境是随机的, 并且我们只观察到有限数量的样本,所以会存在model的偏差,model有可能不是正确的。当环境发生变化的时候,老的model可能无法快速的反应过来,即使修正model,所以我们提出Dyna-Q+的新算法:我们将planning中获得的reward r 修改为r + κ√τ,τ-是某个状态-动作对距离上次访问的时间,越久没访问他的reward就会相应提高,所以就提升了算法的exploration的效果,当环境突然变化了,也能通过探索迅速的修正,167页显示出了Dyna-Q+算法的效果。
8.4节优先扫描。Dyna-Q中模拟经验的初始状态对是随机选取的,这样没有重点的搜索将效率会很低,我们可以优先选取那些Q值变化很大的状态动作对作为模拟经验的开头,这样往下转移到的状态动作对往往都是变化很大的,因为和开头是相关的。这样效率就会提高,170页的图显示出了他的优越性。
8.5更新方式的选择。动态规划用的是期望更新,蒙特卡洛和时间差分用的是样本更新。期望更新需要模型,计算的结果没有采样误差,但是需要考虑下一刻的所有状态动作对,计算量很大,样本更新不需要模型,会有采样误差,但是计算量很小,所以针对状态很多的mdp问题,用样本更新的方法最好。
8.6轨迹采样。这节我们讨论在状态动作对空间中先对哪个状态动作对更新的问题。在动态规划中,我们是在整个状态空间中扫描,每一次扫描对所有的状态只更新一次,这对于状态空间很大的mdp问题来说计算量很大。所以我们在planning中考虑轨迹采样,就是通过策略采样产生模拟经验,对模拟经验上访问过的状态动作对的Q值更新。他的好处一个是计算量少了,第二个就是他导致状态空间中很多没有意义的,基本不会出现的状态动作对被忽视,但它会导致空间的相同旧部分一次又一次地更新。但是在计算资源,时间资源有限的情况下,轨迹采样的表现是非常好的。176页的对比图可以看出。使用了轨迹采样的动态规划称为实时的动态规划real time dynamic progranming。
接下来我把剩下几节的内容(8.8,8.9,8.10,8.11节)合在一起来介绍一个重要的方法---蒙特卡罗树搜索,他就是AlphaGo用到的最主要方法。
蒙特卡洛树搜索的主要目标是:给定一个游戏状态来选择最佳的下一步。和之前我们讲过的基于模型或者不基于模型的learning方法不一样,之前讲的方法都是通过模拟的经验或者现实的经验,直接逐渐改进策略和值函数然后可能把他们记录在表格上,然后去下围棋的时候,通过查表去选择动作,相当于是没有确切目标的盲目的搜索。而我们的MCTS是在决策时刻做planning,他的意思也就是说,我从当前我处于的状态,往前进行一定程度地搜索,做planning,然后估计一下当前状态的各个动作值,然后选择最好的那个动作,提高了搜索效率,将计算资源和时间全部集中在当前的这个状态,是可以真实运用到棋牌类游戏的方法。
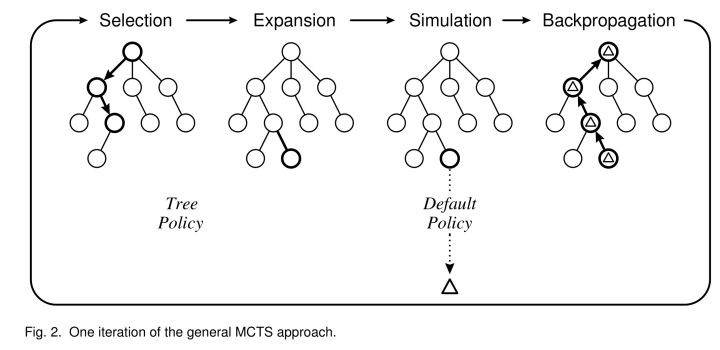
MCTS的算法分为四步。
第一步是Selection,就是在根节点下找到一个最好的值得探索的子节点,首先我们优先选择没有被探索过的子节点,
没有被探索过也就是说没有以它为起点产生过一次模拟经验,也就是说它没有被估值过,当一个根节点下面的所有子节点都是被探索过的,那么我们就称这个根节点 is fully expanded(被完全扩展了)。
如果一个根节点是被完全扩展了的,也就是它的子节点都被探索过。那么我们该如何选择呢?这时候我们就通过tree policy: ε -greedy或UCB(选择UCB值最大的子节点。)来对子节点进行selecion选择。
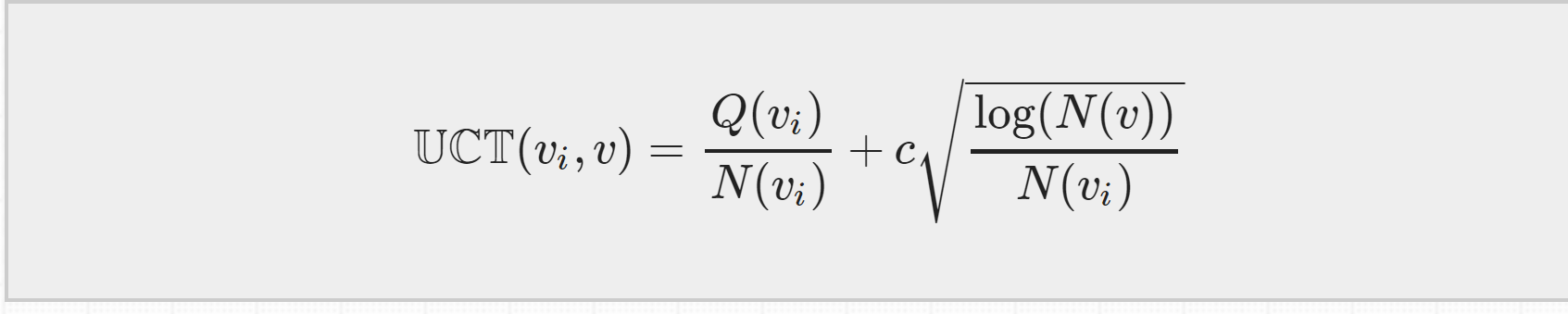
UCT = MCTS + UCB ,等下再来介绍他的公式,只要知道是根据它来选择子节点的就行了。
选择完一个子节点之后,第二步就是expansion。从前面选择到的那个子节点1往下随机走一步创建一个新的子节点2。
第三步就是 simulation,我们以子节点2为起点,使用rollout 算法产生许多条模拟经验,然后立刻像MC一样取各个模拟经验估值的平均来估计出子节点2的值。它和一般的MC不同之处在于,它产生模拟经验不是为了逐步改进策略和值函数,它只关注作为起点的节点,估计出节点的值并使用之后,它会立即丢弃掉这些估计值,所以,rollout算法只是为了更快速地估计出初始节点的值,可以节省更多时间,然后rollout policy默认设置为随机均匀地选择动作。
我们估计出子节点2的值之后,第四步backup,从子节点2开始,一路往回更新子节点1和根节点的值。我们这里的值指的是在回溯过程中,各个节点的累计回报Q值和各个节点被访问的次数N
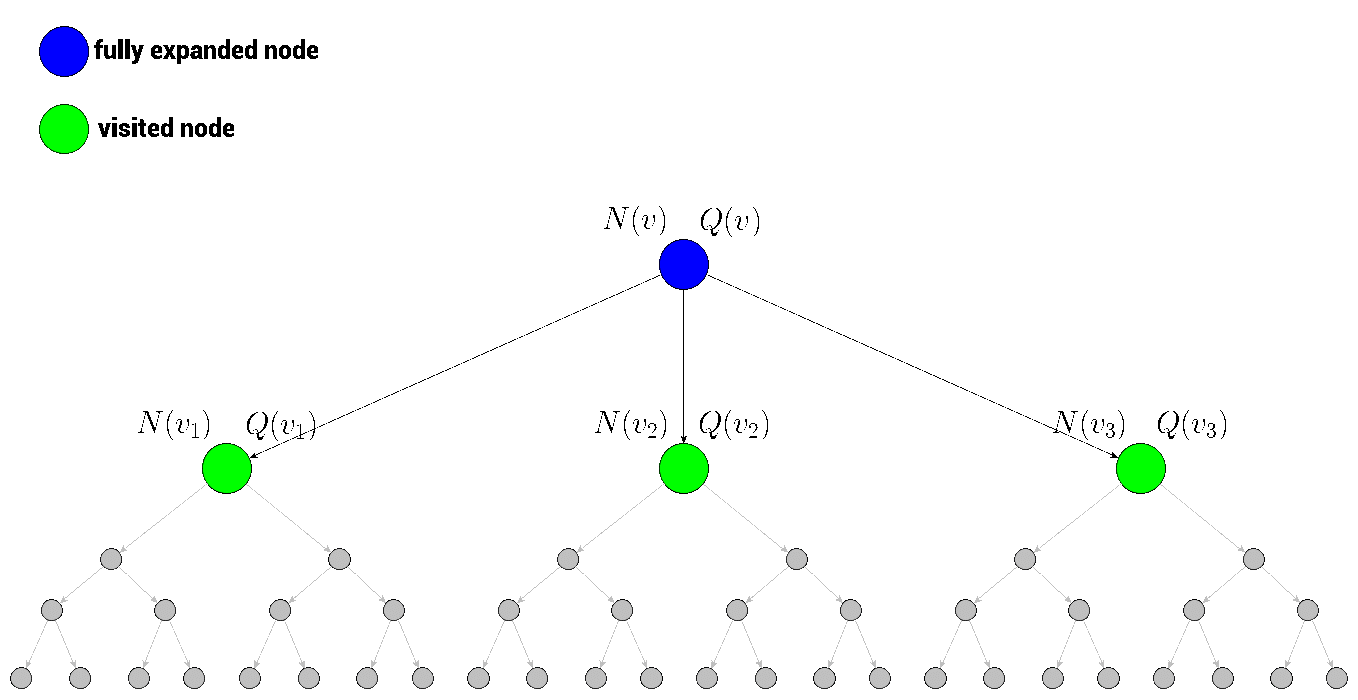
这四步过程会一直持续的迭代,直到达到计算资源、时间资源的极限,迭代就会停止,然后我们就从根节点出发在现实中选择一个最优动作。而选择最优动作的依据就是根据第一步selection中提到的UCB 公式,因为是在MCTS中使用它,我们也把他成为UCT公式
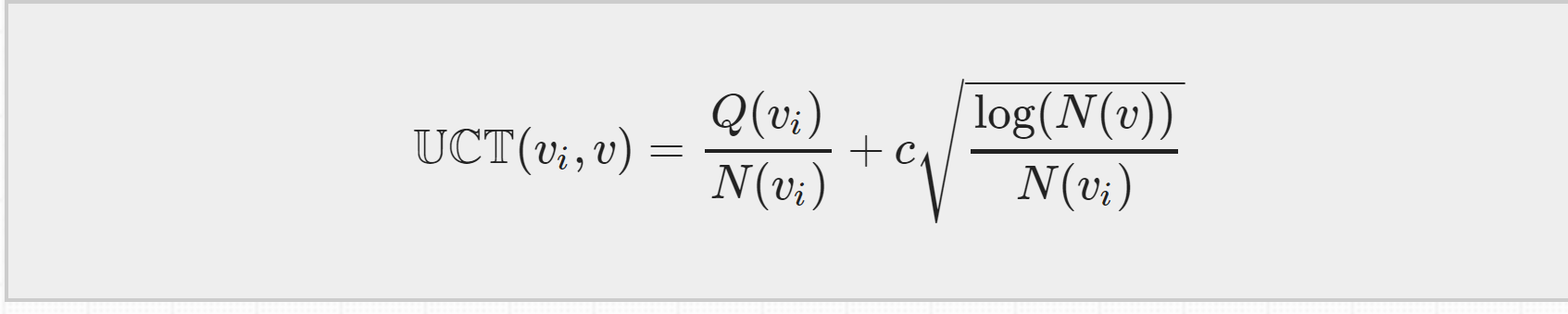
UCT公式分为两个部分:第一部分是exploitation component,各个叶节点的总的汇报Q除以它被访问的次数N,表示的是平均reward,平均reward越大,第一部分的值就越大。
第二部分是exploration component,如果某个叶节点的访问次数越少,第二部分的值就会越大。
所以这个公式平衡了探索和开发,不会陷入局部最优的情况。
所以当我们结束迭代的时候,哪一个叶节点的UCT值最大,我们在现实中就选择这个最优动作。**
MCTS整个的基本思路就是这样,我们首先从根节点(也就是我们现实中处于的状态)根据tree policy选择一个值得探索的叶节点1,然后从叶节点1往下扩展一步,来到了叶节点2,然后以叶节点2为起点,开始用rollout policy产生模拟经验,得到Q和N的信息,然后一路backup回去更新各个母节点的UCT值,不断地重复这一过程直到计算资源和时间耗尽,我们就选择UCT值最大的那个动作,移动到一个叶节点,整个叶节点就又变成了一个根节点,重复上面的过程展开成一棵树,进行动作的选择。
--------------------------------------------------------------------------------------------------