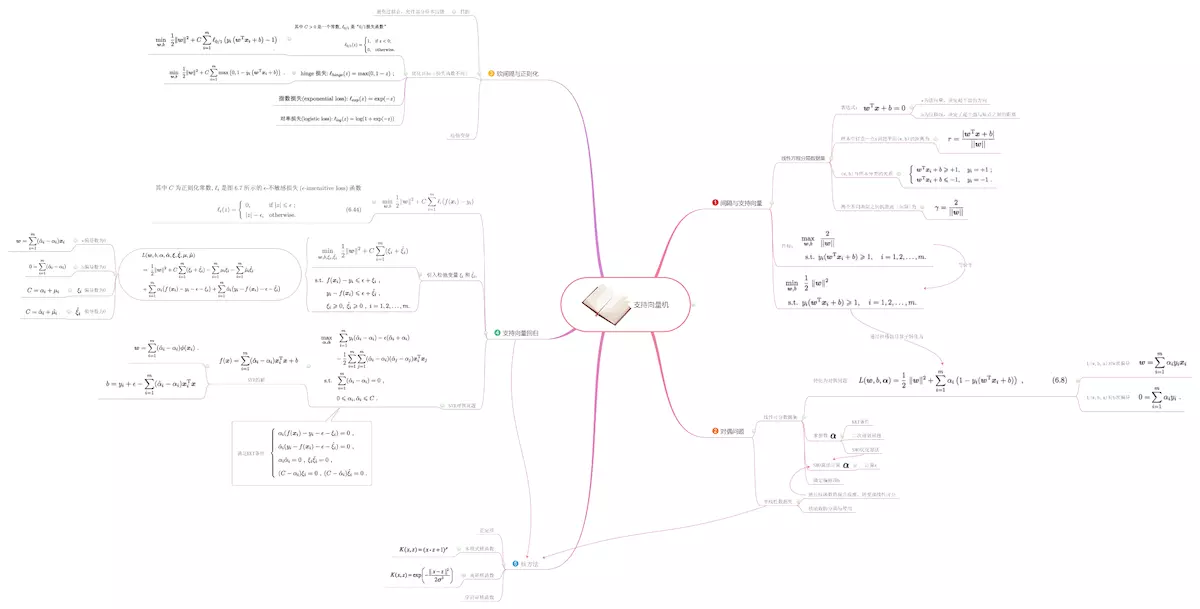
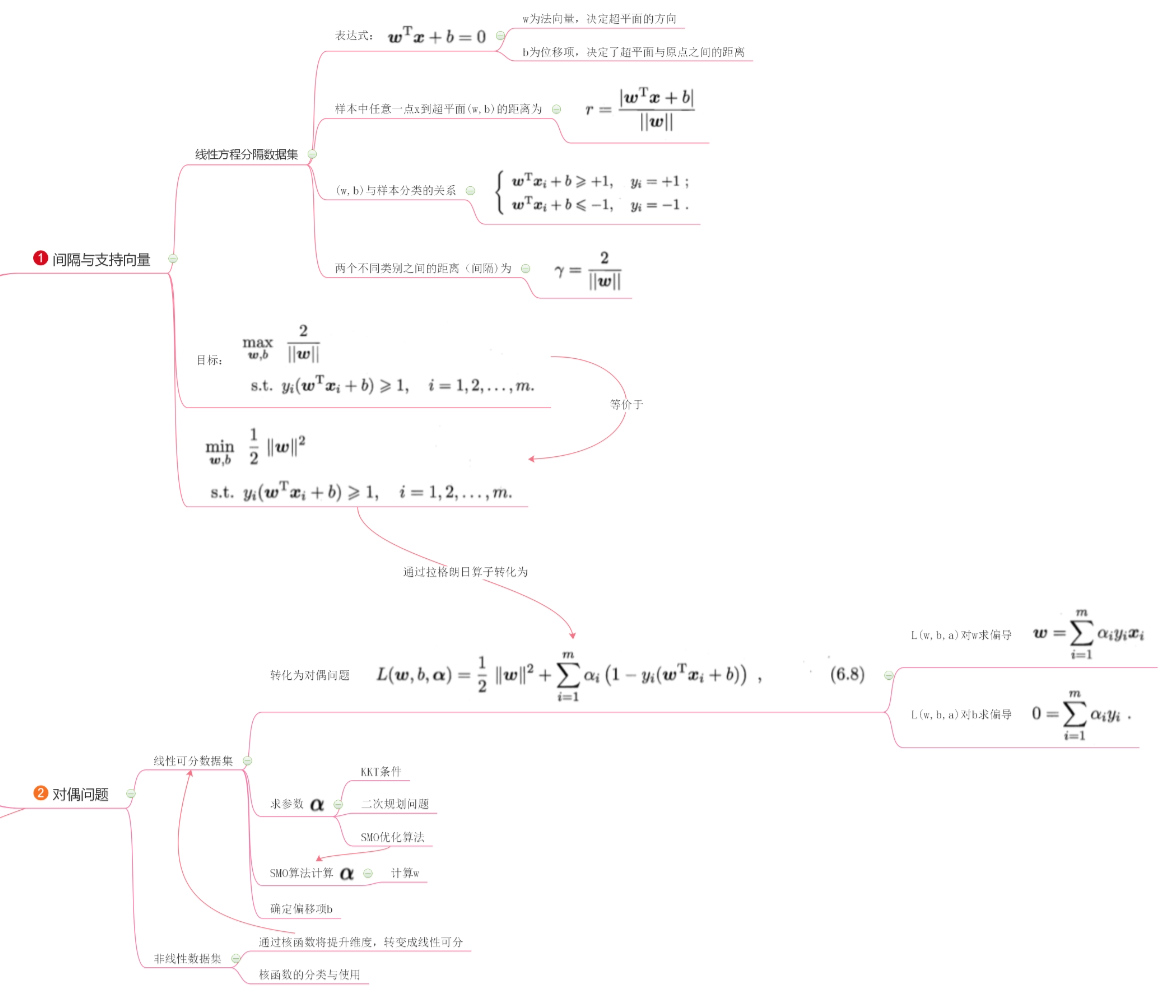
1. 间隔与支持向量

1.1 几个概念

支持向量机与感知机类似，都是在样本空间中找到划分超平面，将不同类别的样本分开。在样本空间中，划分超平面可以使用线性方程进行描述：

\begin{align}
0=\boldsymbol{w}^T \boldsymbol{x}+b\tag{1.1}
\end{align}

其中， $\boldsymbol{w}=[w_1, w_2, ..., w_m]$ 为法向量，决定了超平面的方向， $b$ 为位移项，决定了超平面距离原点的位置。

一般来说， $| \boldsymbol{w}^T \boldsymbol{x_i}+b|$ 决定了点 $x_i$ 到超平面的距离； $\boldsymbol{w}^T \boldsymbol{x_i}+b$ 与 $y_i$ 的符号是否一致决定了分类是否正确。

另外，做以下定义：函数间隔、几何间隔、间隔、支持向量。

1.1.1函数间隔 $\hat \gamma$

对于给定的训练数据集 $T=[(\boldsymbol{x_1}, y_1), (\boldsymbol{x_2}, y_2), ..., (\boldsymbol{x_N}, y_N)]$ 和超平面 $(\boldsymbol{w}, b)$ ，定义超平面 $(\boldsymbol{w}, b)$ 关于样本点 $(\boldsymbol{x_i}, y_i)$ 的函数间隔为

\begin{align}
\hat \gamma_i = y_i(\boldsymbol{w}^T \boldsymbol{x_i}+b)\tag{1.2-1}
\end{align}

令：

\begin{align}
\hat \gamma =\min_{i=1,2,...,N} \gamma_i \tag{1.2-2}
\end{align}

1.1.2 几何间隔 $\gamma$

当我们成比例的改变 $w$ 和 $b$ 时，函数间隔也会发生等比例的变化，因此，对分离超平面的法向量 $w$ 规范化，令其模长为1，使得间隔确定，此时称为几何间隔。

1.1.3 支持向量

间隔 $\gamma$ 越大，说明不同类分的越开，因此可以把目标理解为：

\max _{w, b} \gamma=\frac{\hat \gamma}{||\boldsymbol{w}||}\\
s.t. \ y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b) \geq \hat \gamma
\tag{1.3}

而在公式(1.5)中， $\hat \gamma$ 为何值并不影响最后的求解，因为 $\hat \gamma$ 与 $\boldsymbol{w},b$ 成比例变化。因此，取 $\hat \gamma=1$ 。那么，若存在 $\boldsymbol{x_k}, k=1,2,...,l; l<N$ ，距离超平面最近，有 $y_k(\boldsymbol{w}^T \boldsymbol{x_k}+b)=1$ ，那么这 $k$ 个训练样本点被称为支持向量。其中两个异类支持向量到超平面的距离之和为： $2\gamma=\frac{2}{||\boldsymbol{w}||}$

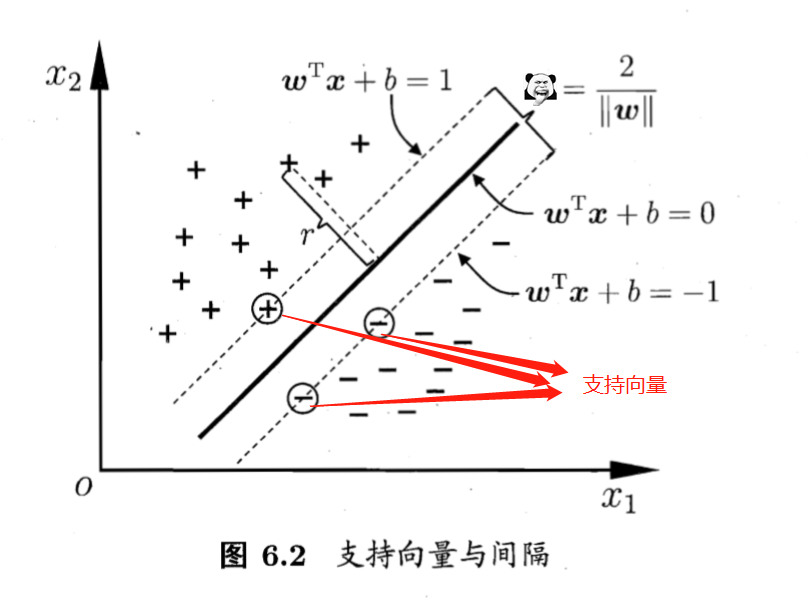
1.2 小结

其实这一部分与感知机没啥区别，就是定义了几个概念：函数间隔，几何间隔，支持向量。
观察图6.2可知，决定参数 $\boldsymbol{w},b$ 的其实就只有支持向量这 $l$ 个点，其他的点你皮任你皮，对我模型结果毫无影响。

2. 问题优化

2.1 确定目标

公式(1.5)就可以理解为：即要求（2只是一个系数，不用过分在意）

\begin{align}
\max _{w, b} \frac{2}{||\boldsymbol{w}||} \Leftrightarrow \min _{w, b} \frac{1}{2} ||\boldsymbol{w}||^2 \\
s.t. \ y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b) \geq 1
\tag{2.1}
\end{align}

引入拉格朗日乘子，构造拉格朗日函数，借助对偶问题(啥是对偶问题？)，有：

\begin{align}
L(w,b,\alpha) = \frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^{N}\alpha_i (1-y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b))
\tag{2.2}
\end{align}

分别计算 $L(\boldsymbol{w},b,\alpha)$ 对 $w$ 和 $b$ 求导，并令其为 $0$ ：

\left\{\begin{matrix}
\boldsymbol{w} =& \sum_{i=1}^{N}\alpha_i y_i \boldsymbol{x_i} \\
0=& \sum_{i=1}^{N}\alpha_i y_i
\end{matrix}\right.
\tag{2.3}

将(2.3)代入(2.2)，则有：

\begin{align}
\max _{\alpha} L(w,b,\alpha) &= \frac{1}{2} \sum_{i=1}^{N}\alpha_i y_i \boldsymbol{x_i}\sum_{j=1}^{N}\alpha_j y_j \boldsymbol{x_j} + \sum_{i=1}^{N}\alpha_i (1-y_i(\sum_{j=1}^{N}\alpha_j y_j \boldsymbol{x_j^T}·\boldsymbol{x_i}+b)) \\
&=\frac{1}{2} \sum_{i=1}^{N}\alpha_i y_i \boldsymbol{x_i}\sum_{j=1}^{N}\alpha_j y_j \boldsymbol{x_j} - \sum_{i=1}^{N}\alpha_i y_i \boldsymbol{x_i}\sum_{j=1}^{N}\alpha_j y_j \boldsymbol{x_j} + \sum_{i=1}^{N}\alpha_i y_ib+\sum_{i=1}^{N}\alpha_i \\
&=\sum_{i=1}^{N}\alpha_i - \frac{1}{2} \sum_{i=1}^{N}\alpha_i y_i \boldsymbol{x_i}\sum_{j=1}^{N}\alpha_j y_j \boldsymbol{x_j}\\
&=\sum_{i=1}^{N}\alpha_i - \frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j \boldsymbol{x_i^T}\boldsymbol{x_j}
\tag{2.4} \\
s.t \sum_{i=1}^{N} \alpha_i y_i=0, \\
\alpha_i \geq 0
\end{align}

根据(啥是对偶问题?)可知，公式(2.4)的KKT条件为：

\left\{\begin{matrix}
\alpha_i \geq 0 \\
1-y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b) \leq 0 \\
\alpha_i (1-y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)) = 0, i=1,2,...,N
\end{matrix}\right.
\tag{2.4.1}

2.2 换个角度

求公式(2.4)的最大等价于求公式(2.5)的最小：

\begin{align}
\min_{\alpha} L(w,b,\alpha) &=\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j \boldsymbol{x_i^T}\boldsymbol{x_j} - \sum_{i=1}^{N}\alpha_i
\tag{2.5} \\
s.t \sum_{i=1}^{N} \alpha_i y_i=0, \\
\alpha_i \geq 0
\end{align}

接下来，如果解出每一个 $\alpha$ 就可以算出 $\boldsymbol{w}$ 。具体怎么求，稍后再说。

又因为前面提过：若存在 $\boldsymbol{x_k}, k=1,2,...,l; l<N$ ，距离超平面最近，有 $y_k(\boldsymbol{w}^T \boldsymbol{x_k}+b)=1$ ，那么这 $k$ 个训练样本点被称为支持向量。其中两个异类支持向量到超平面的距离之和为： $2\gamma=\frac{2}{||\boldsymbol{\boldsymbol{w}}||}$

所以，在已知了每一个 $\alpha$ 之后，可以计算出 $\boldsymbol{w}, b$ 分别为：

\left\{\begin{matrix}
\boldsymbol{w} =& \sum_{i=1}^{N}\alpha_i y_i \boldsymbol{x_i} \\
b =& y_k-\boldsymbol{w}^T\boldsymbol{x_k}
\end{matrix}\right.
\tag{2.6}

其中 $\boldsymbol{x_k}$ 为支持向量样本中的任意一个值。为了保持鲁棒性， $b$ 使用所有支持向量计算其均值，因此：

\left\{\begin{matrix}
\boldsymbol{w} =& \sum_{i=1}^{N}\alpha_i y_i \boldsymbol{x_i} \\
b =& \frac{1}{l}\sum_{k=1}^{l} (y_k-\boldsymbol{w}^T\boldsymbol{x_k})
\end{matrix}\right.
\tag{2.7}

其中， $N$ 样本空间的大小， $l$ 为所有支持向量组成的样本空间大小， $\boldsymbol{w}$ 是一个 $1*d$ 维的向量。

留疑！！！

问题1：到目前为止，计算出的 $\boldsymbol{w}$ 和 $b$ 都没有体现： "决定参数 $\boldsymbol{w},b$ 的其实就只有支持向量这 $l$ 个点，其他的点你皮任你皮，对我模型结果毫无影响。" 的合理性，不知道最后算法计算后的 $\alpha$ 结果是不是能体现。。。

问题2：西瓜书中的 $b$ 的计算，个人感觉西瓜书125页公式(6.17)是有点奇怪的。书中的 $\boldsymbol{w}$ 是在整个样本空间上计算得出的（这个没问题），但是 $b$ 却通过支持向量计算得出的 $\boldsymbol{w}$ 代入公式(2.6)计算得出。

解答：

问题1：记 $\boldsymbol{\alpha}=(\alpha_1, \alpha_2, ..., \alpha_N)$ 为最后的计算结果，在这个计算结果中，一定有一个值（记为 $\alpha_{k'}$ ）满足 $\alpha_{k'}>0$ ，而且有其所对应的 $(\boldsymbol{x_{k'}}, y_{k'})$ 正好满足 $y_{k'}(\boldsymbol{w}^T \boldsymbol{x_{k'}}+b)=1$ 。

为什么一定有一个 $\alpha_{k'}>0$ ? 反证法：假设 $\boldsymbol{\alpha}=\boldsymbol{0}$ ，那么根据公式(2.6)，有 $\boldsymbol{w}=\boldsymbol{0}$ ，在拉格朗日乘子、KKT条件与对偶问题中提到过，如果拉格朗日乘子为0，说明所有的点都在限制条件所构成函数边界的内部，也就不存在什么支持向量了。所以，一定有一个 $\alpha_{k'}>0$ 。

为什么 $y_{k'}(\boldsymbol{w}^T \boldsymbol{x_{k'}}+b)=1$ ？ KKT的互补条件(公式2.4.1)： $\alpha_i(1-y_i(\boldsymbol{w}^T \boldsymbol{x_i}+b))=0$ ，那么，在 $\alpha_{k'}>0$ 的情况下，要满足条件，只能有 $y_{k'}(\boldsymbol{w}^T \boldsymbol{x_{k'}}+b)=1$ 。这不就是支持向量吗！！！

问题2：《统计学习方法》里面是整个样本空间，不是支持向量构成的样本空间，而且西瓜书里没交代 $m$ 是什么鬼，所以单方面宣布是笔误好了qwq。

3. 线性支持向量机和软间隔最大化

3.1 线性支持向量机

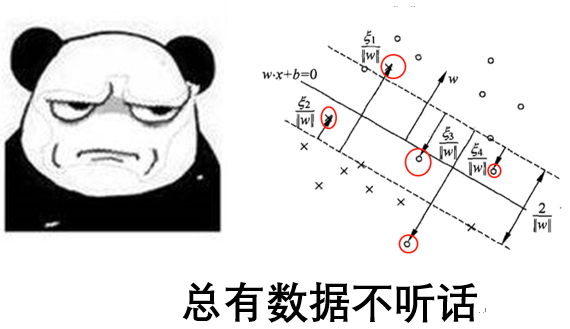
训练集中总有数据（记为 $(\boldsymbol{x_u}, y_u)$ ）不能满足 $y_u(\boldsymbol{w}^T \boldsymbol{x_u}+b) \geq 1$ 这个条件（红圈中的点），删又不能删，只好帮他一把，修改一下底线，引入松弛变量 $\xi \geq 0$ 。这种修改底线的做法，叫做软间隔，原先叫做硬间隔。

这样，就有了：线性支持向量机（我要吐槽一句，不知道谁取的名字，误导性炒鸡强，人家本意原来是：数据集为线性不可分时的线性支持向量机。。。）

为了使软间隔最大化，限制条件变为：

\begin{align}
\ y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b) \geq 1-\xi_i
\tag{3.1}
\end{align}

目标函数变为，

\begin{align}
&\min _{w, b} \frac{1}{2} ||\boldsymbol{w}||^2 + C\sum_{i=1}^{N}\xi_i\\
s.t. &\ y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b) \geq 1-\xi_i, i=1,2,...,N \\
&\xi_i \geq 0, i=1,2,...,N
\tag{3.2}
\end{align}

其中，这里， $C>0$ 称为惩罚参数，一般由应用问题决定， $C$ 值大时对误分类的惩罚增大， $C$ 值小时对误分类的惩罚减小。最小化目标函数(1.2)包含两层含义：

$\frac{1}{2}||\boldsymbol{w}||$ 尽量小，即间隔尽量大。
使误分类点的个数尽量小，C是调和二者的系数。

3.2 确定目标

引入拉格朗日乘子，构造朗格朗日函数：

\begin{align}
L(\boldsymbol{w}, b, \xi, \alpha, \mu) = \frac{1}{2}||\boldsymbol{w}||^2 + C\sum_{i=1}^{N}\xi_i - \sum_{i=1}^{N} \alpha_i (y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)-1+\xi_i) - \sum_{i=1}^{N} \mu_i \xi_i\tag{3.3}
\end{align}

公式(3.3)分别对 $\boldsymbol{w}, b, \xi$ 求导：

\left\{\begin{matrix}
\triangledown_{\boldsymbol{w}}L(\boldsymbol{w}, b, \xi, \alpha, \mu) =& \boldsymbol{w} - \sum_{i=1}^{N} \alpha_i y_i \boldsymbol{x_i} \\
\triangledown_{b}L(\boldsymbol{w}, b, \xi, \alpha, \mu) =& \sum_{i=1}^{N}\alpha_i y_i \\
\triangledown_{\xi_i}L(\boldsymbol{w}, b, \xi, \alpha, \mu) =& C-\alpha_i-\mu_i \\
\end{matrix}\right.
\tag{3.4}

令(3.4)中三式均为0，代入公式(3.3)中有：

\begin{align}
\min_{\alpha} L(w,b,\alpha) &=\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j \boldsymbol{x_i^T}\boldsymbol{x_j} - \sum_{i=1}^{N}\alpha_i
\tag{3.5} \\
s.t. &\sum_{i=1}^{N} \alpha_i y_i=0, \\
& C-\alpha_i-\mu_i=0, \\
&\alpha_i \geq 0, \\
&\mu_i \geq 0, i=1,2,...,N
\end{align}

因为我们的重点是求 $\alpha$ ，所以对 $\alpha$ 的限制条件越多越好，所以公式(3.5)又可以写成

\begin{align}
\min_{\alpha} L(w,b,\alpha) &=\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j \boldsymbol{x_i^T}\boldsymbol{x_j} - \sum_{i=1}^{N}\alpha_i
\tag{3.6}\\
s.t. &\sum_{i=1}^{N} \alpha_i y_i=0, \\
& C \geq \alpha_i \geq 0, i=1,2,...,N
\end{align}

3.3 线性支持向量机的支持向量

在下图中，分离超平面由实线表示，间隔边界由虚线表示，正例点由“。”表示，负例点由“×”表示。

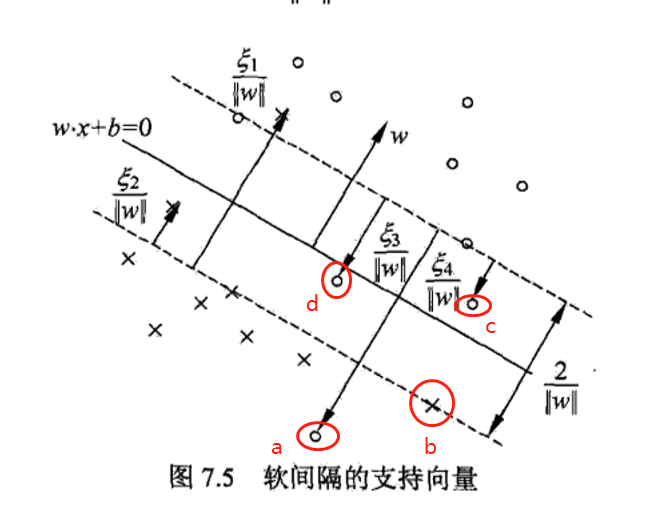
留疑！！！ abcd这些点与 $\alpha_i$ 之间的对应状态是怎样的？

解答先看看公式(2.2)和公式(3.3)：

\begin{align}
L(w,b,\alpha) =& \frac{1}{2}||\boldsymbol{w}||^2 + \sum_{i=1}^{N}\alpha_i (1-y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)) \\
=& \frac{1}{2}||\boldsymbol{w}||^2 - \sum_{i=1}^{N}\alpha_iy_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b) + \sum_{i=1}^{N}\alpha_i
\tag{2.2}
\end{align}

\begin{align}
L(\boldsymbol{w}, b, \xi, \alpha, \mu)
=& \frac{1}{2}||\boldsymbol{w}||^2 + C\sum_{i=1}^{N}\xi_i - \sum_{i=1}^{N} \alpha_i (y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)-1+\xi_i) - \sum_{i=1}^{N} \mu_i \xi_i \\
=&\frac{1}{2}||\boldsymbol{w}||^2-\sum_{i=1}^{N} \alpha_i y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)+\sum_{i=1}^{N} \alpha_i+(C-\alpha_i-\mu_i)\sum_{i=1}^{N}\xi_i
\tag{3.3}
\end{align}

其KKT条件为：

\left\{\begin{matrix}
\alpha_i \geq 0, \mu_i \geq 0 \\
y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)-1+\xi_i \geq 0\\
\alpha_i(y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)-1+\xi_i) = 0 \\
\xi_i \geq 0,\mu_i \xi_i=0
\end{matrix}\right.

根据(啥是对偶问题?)可知：

若 $\alpha=0$ 则点不会对 $(\boldsymbol{w}^T·\boldsymbol{x_i}+b)$ 有影响，故而是大部分远离支持向量且正确分类的点，有 $y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b) > 1-\xi_i$ 。

若 $\alpha>0$ ，则说明必有 $y_i(\boldsymbol{w}^T·\boldsymbol{x_i}+b)=1-\xi_i$ 。

若 $C>\alpha>0$ ，因为 $C=\alpha_i+\mu_i$ ，所以 $\mu_i>0$ ，则 $\xi_i=0$ ，此时为支持向量，如b点。

若 $C=\alpha$ ，因为 $C=\alpha_i+\mu_i$ ，所以 $\mu_i=0$ ，则有：

若 $1\geq \xi_i>0$ ，此时落在最大间隔内部，如c点。

若 $\xi_i>1$ ，此时误分类，如a,d点。

4. 核技巧

4.1 核技巧之劳动改造

上面的数据集都有一个要求：那就是数据集线性可分，再不济也要基本可分（即大部分的点要线性可分），但是，如果数据集超出了容忍的底线怎么办？比如过像这样，下图这类数据集就GG了。

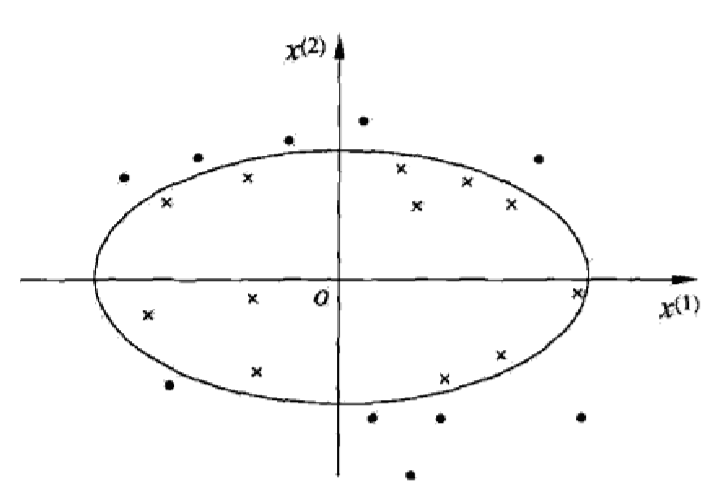
对于这种不听话的数据集，我们需要对其进行改造：具体咋改造呢？请参见核技巧。改造之后的数据集如何使用呢？观察到在公式(3.6)中，

只涉及输入实例与实例之间的内积。因此，可以用使用核函数 $K(x_i,x_j)=(\phi(x_i),\phi(x_j))$ 代替，此时，公式(3.6)变为

\begin{align}
\min_{\alpha} L(w,b,\alpha) &=\frac{1}{2} \sum_{i=1}^{N}\sum_{j=1}^{N}\alpha_i \alpha_j y_i y_j K(\boldsymbol{x_i}, \boldsymbol{x_j}) - \sum_{i=1}^{N}\alpha_i
\tag{4.1} \\
s.t. &\sum_{i=1}^{N} \alpha_i y_i=0, \\
& C \geq \alpha_i \geq 0, i=1,2,...,N
\end{align}

这样，经过映射函数将原来的输入空间变换到一个新的特征空间，将输入空间中的内积 $(\boldsymbol{x_i^T}·\boldsymbol{x_j})$ ，变换为特征空间中的内积 $K(\boldsymbol{x_i}, \boldsymbol{x_j})$ ，在新的特征空间里从训练样本中学习线性支持向量机。当映射函数是非线性函数时，学习到的含有核函数的支持向量机是非线性分类模型。

4.2 核技巧之重返社会

5. 问题求解

观察公式(2.5)和公式(4.1)，可知，该问题是一个二次规划问题^[1]，使用Sequential Minimal Optimization(SMO)算法求解。

5.1 SMO基本思路

先固定除了 $\alpha_{u_1}$ 之外的所有参数值，求 $\alpha_{u_1}$ 上的极值，由于有 $\sum_{i=1}^{N} \alpha_i y_i=0$ 的约束条件，因此，另一个参数值 $\alpha_{u_2}$ 也可以用 $\alpha_{u_1}$ 表示，因此，SMO方法一次可以优化两个参数 $\alpha_{u_1}$ 和 $\alpha_{u_2}$ ，并固定其他参数。

###5.2 基本流程：

选取一对待更新的变量 $\alpha_{u_1}$ 和 $\alpha_{u_2}$ 。
固定 $\alpha_{u_1}$ 和 $\alpha_{u_2}$ 之外的所有变量，求解公式(3.7)。

书上的简单例题。

6. 小结

线性支持向量机的算法总结流程图如下：

7. 参考文献

《统计学习方法》《西瓜书》

注脚——凸二次规划问题：
仿射函数即由 1 阶多项式构成的函数，一般形式为 $f(x)=\boldsymbol{A^Tx+b}$ ，这里， $\boldsymbol{A}$ 是一个 $m×k$ 矩阵， $\boldsymbol{x}$ 是一个 $k$ 维向量， $\boldsymbol{b}$ 是一个 $m$ 维向量，实际上反映了一种从 $k$ 维到 $m$ 维的空间映射关系。 ↩︎