数据结构之线性表--链式存储结构--单链表

sako
2,967 阅读5分钟

定义

线性表的链式存储结构，是用一组任意的存储单元来存储线性表的数据元素，这些单元可以分散在内存中的任意位置，即不要求逻辑上相邻的两个元素在物理上也相邻;而是通过“链”建立起数据元素之间的逻辑关系。

  • 由于在物理上不一定相邻，因此每个数据元素，除了存储本身的信息之外，还需要存储指示其直接后继的信息;
  • 存储数据元素信息的域称为数据域；
  • 存储直接后继位置的域称为指针域，其中的信息称为指针或链；
  • 数据域和指针域组合起来，称为结点；
  • n个结点链接成一个链表，即为线性表(a1, a2, a3, …, an)的链式存储结构；
  • 一般情况下，链表中每个结点可以包含若干个数据域和若干个指针域。如果每个结点中只包含一个指针域，则称其为单链表；
  • 链表中的第一个结点（或者头节点）的存储位置叫做头指针，最后一个结点指针为空(NULL)；
  • 为了便于实现各种操作，可以在单链表的第一个结点之前增设一个结点，称为头结点。

单链表用go语言描述如下：

type data interface{}

type Node struct {
	Data data // 数据域
	Next *Node // 指针域
}

type LinkList struct {
	Head *Node
	len int
}

// 初始化一个链表
func New() *LinkList {
	l := &LinkList{Head: &Node{}}
	l.len = 0
	return l
}

主要操作

查找

查找分为按值查找，和按序号查找，不过在算法的思想上基本是一致的：

1、从表头开始找，判断当前节点是否满足查找条件;

2、如果不满足，则将指针后移一位，指向下一个结点，继续判断条件;

3、找到满足查找条件的结点，则退出循环，返回该结点，如果没找到，则返回null

//  按序号查找
func (l *LinkList) FindKth(k int) *Node {
	if k < 1 || k > l.len {
		return nil
	}
	current := l.Head
	for i := 1; i <= k; i++ {
		current = current.Next
	}
	return current
}

// 按值查找
func (l *LinkList) Find(value data) *Node {
	for current := l.Head; current != nil; current = current.Next {
		if current.Data == value {
			return current
		}
	}
	return nil
}
  • 两个算法的时间复杂度为O(n)
  • 循环中都使用到了“工作指针后移”，这也是很多算法的常用技术

插入

在第i-1(1<=i<=n+1)个结点之后插入一个值为X的新结点，算法思想：

1、构建一个新的结点s；

2、找到第i-1个结点p；

3、修改指针，插入新的结点。

其中第3步，我们用图表示：

上图的操作可以得出下面两行代码

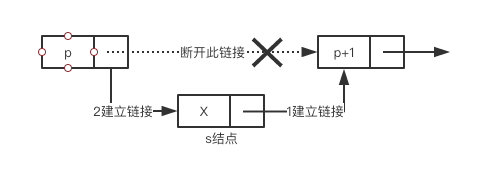
s.Next = p.Next // 1处建立链接
p.Next = s // 2处建立链接

如果将这两行代码的顺序交换一下会怎么样？

先执行p.Next = s，这个时候就p.Next指向了s结点，然后执行s.Next = p.Next，但是p.Next已经是s结点了，因此也就变成了s.Next = s。这个时候插入就会失败。所以这两句是无论如何不能弄反的。

func (l *LinkList) Insert(value data, i int) bool {
	preNode := l.FindKth(i - 1)
	if preNode == nil {
		return false
	}
	node := &Node{Data: value}
	node.Next = preNode.Next
	preNode.Next = node
	l.len++
	return true
}
  • 算法的时间复杂度取决了i位置，因此为O(n)

删除

删除链表的第i(1<=i<=n)个位置的结点，算法思想：

1、找到第i-1个结点，为p;

2、用s保存p.Next的结点，即第i个结点;

3、将p.Next指向s.Next，断开结点的链接;

4、用e保存s的值，释放s结点，返回e。

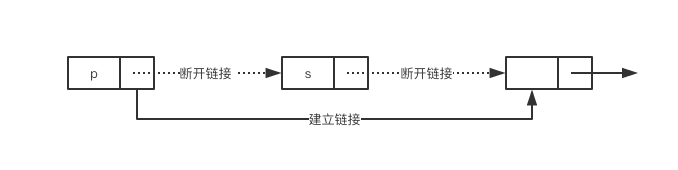
func (l *LinkList) Delete(i int) (data, bool) {
	preNode := l.FindKth(i - 1)
	if preNode == nil {
		return nil, false
	}
	deleteNode := preNode.Next
	preNode.Next = deleteNode.Next
	value := deleteNode.Data
	deleteNode = nil
	l.len--
	return value, true
}
  • 算法的时间复杂度取决了i位置，因此为O(n)

整表创建

我们可以使用头插法，或者尾插法的方式，创建链表。

头插法

即在创建链表时，每个元素都按顺序的插在表头。

1、给链表添加一个在表头插入一个元素的方法，称为InsertHead;

2、依次使用InsertHead将元素加入链表中。

func (l *LinkList) InsertHead(value data) {
	node := &Node{Data: value}
	node.Next = l.Head.Next
	l.Head.Next = node
	l.len++
}

// 头插法创建
l := LinkList.New()
for i := 1; i <= 5; i++ {
    // 将1到5依次插入表头
    l.InsertHead(i)
}

查看链表的结构：

可以看的出来，使用头插法创建的链表，存储的顺序是反向的。

尾插法

即在创建链表时，每个元素都按顺序的插在表尾。

1、给链表添加一个在表头插入一个元素的方法，InsertTail;

2、依次使用InsertTail将元素加入链表中。

func (l *LinkList) InsertTail(value data) {
	node := &Node{Data: value}
	current := l.Head
	for current.Next != nil {
		current = current.Next
	}
	current.Next = node
	l.len++
}

// 尾插法创建
l := LinkList.New()
for i := 1; i <= 5; i++ {
    // 将1到5依次插入表尾
	l.InsertTail(i)
}

链表结构：

总结

我们从时间和空间上对比一下线性表的链式存储与顺序存储:

时间

查找：

  • 顺序存储结构O(1)
  • 单链表O(n)

插入和删除：

  • 顺序存储结构需要平均移动表长一半的元素，时间为O(n)
  • 单链表在计算出某位置的指针后，插入和删除时间仅为O(1)
  • 比如，在第i个位置，连续插入10个元素，对于顺序存储，每次插入都要移动后面的元素，所以每次都是O(n)
  • 而单链表，只有在第一次的时候要找到i位置，即O(n)，之后的插入都是O(1)

空间

  • 顺序存储结构需要预先分配空间，如果分配大了，会造成空间浪费，如果分配小了，可能产生溢出
  • 单链表不需要预先分配空间，只要还用空间就可以进行分配，元素个数也不受限制

结语

  • 如果线性表需要频繁查找，很少进行插入和删除，则适合用顺序存储；
  • 如果需要频繁的插入和删除，则适合用单链表；
  • 如果事先知道线性表的长度，则适合使用顺序存储，反之，可以使用单链表；
  • 没有银弹——总之，两者各有优缺点，我们应当根据实际情况，选择合适的存储结构。

Thanks!

avatar
文章
阅读
粉丝