决策树是一种树形结构,其中每个内部节点表示一个属性上的测试,每个分支代表一个测试输出,每个叶节点代表一种类别。
划分选择
决策树学习最关键的在于如何选择最优划分属性。一般而言,随着划分过程不断进行,我们希望决策树的分支节点所包含的样本尽可能属于同一类别,即结点的“纯度”越来越高
信息增益
假定当前样本集合 D 中第 k 类样本所占的比例为 ,则 D 的信息熵定义为
假定离散属性 a 有 V 个可能的取值 ,若使用 a 来对样本集 D 进行划分,则会产生 V 个分支结点,其中第 v 个分支结点包含了 D 中所有在属性 a 上取值为
的样本,记为
.信息增益定义为
一般而言,信息增益越大,则意味着使用属性 a 来进行划分所获得的“纯度提升”越大
ID3决策树学习算法就是以信息增益为准则来选择划分属性的。
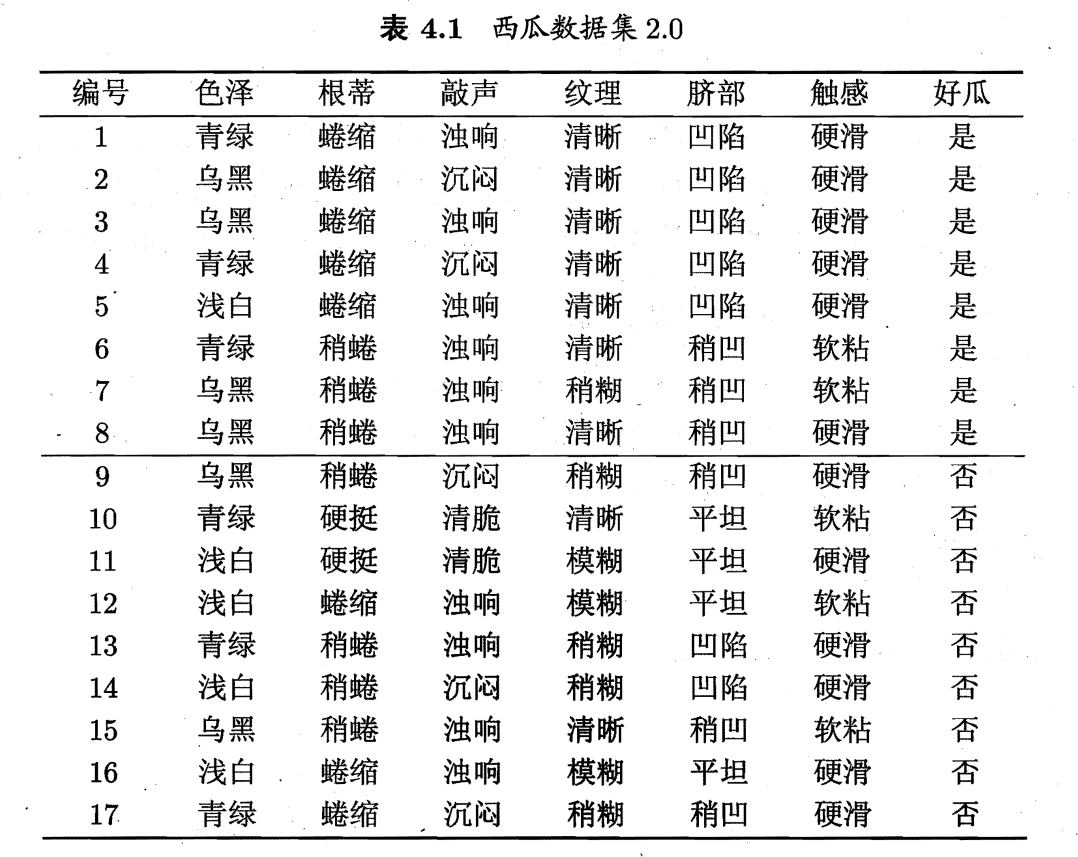
如上表,显然,,其中,正例占
,反例占
,可计算根节点的信息熵为
以属性“色泽”为例,它有 3 个可能的取值:{青绿,乌黑,浅白}。使用该属性对 D 进行划分,则可得到 3 个子集,分别记为:
子集包含编号为 {1, 4, 6, 10, 13, 17}的 6 个样例,其中正例占
,反例占
;
包含编号为 {2, 3, 7, 8, 9, 15} 的 6 个样例,其中正、反例分别占
;
包含编号为 {5, 11, 12, 14, 16} 的 5 个样例,其中正、反例分别占
.计算出用“色泽”划分之后所获得的 3 个分支结点的信息熵为
于是,得到属性“色泽”的信息增益为
类似的,计算出其他属性的信息增益:
属性“纹理”的信息增益最大,于是他被选为划分属性.
增益率
增益率定义为
其中
C4.5决策树算法使用增益率来选择最优划分属性
基尼指数
数据集 D 的纯度可用基尼值来度量:
Gini(D) 越小,数据集 D 的纯度越高
属性 a 的基尼指数定义为
在候选属性集合 A 中,选择使得划分后基尼指数最小的属性作为最优划分属性
CART 决策树采用“基尼指数”来选择划分属性
剪枝处理
剪枝是决策树学习算法对付“过拟合”的手段。决策树剪枝策略有“预剪枝”和“后剪枝”
预剪枝是指在决策树生成过程中,对每个结点在划分前先进行估计,若当前结点的划分不能带来决策树泛化性能提升,则停止划分并将当前结点标记为叶节点;后剪枝则是先从训练集生成一颗完整的决策树,然后自底向上地对非叶节点进行考察,若将该结点对应的子树替换为叶节点能带来决策树泛化性能的提升,则将该子树替换为叶节点
预剪枝
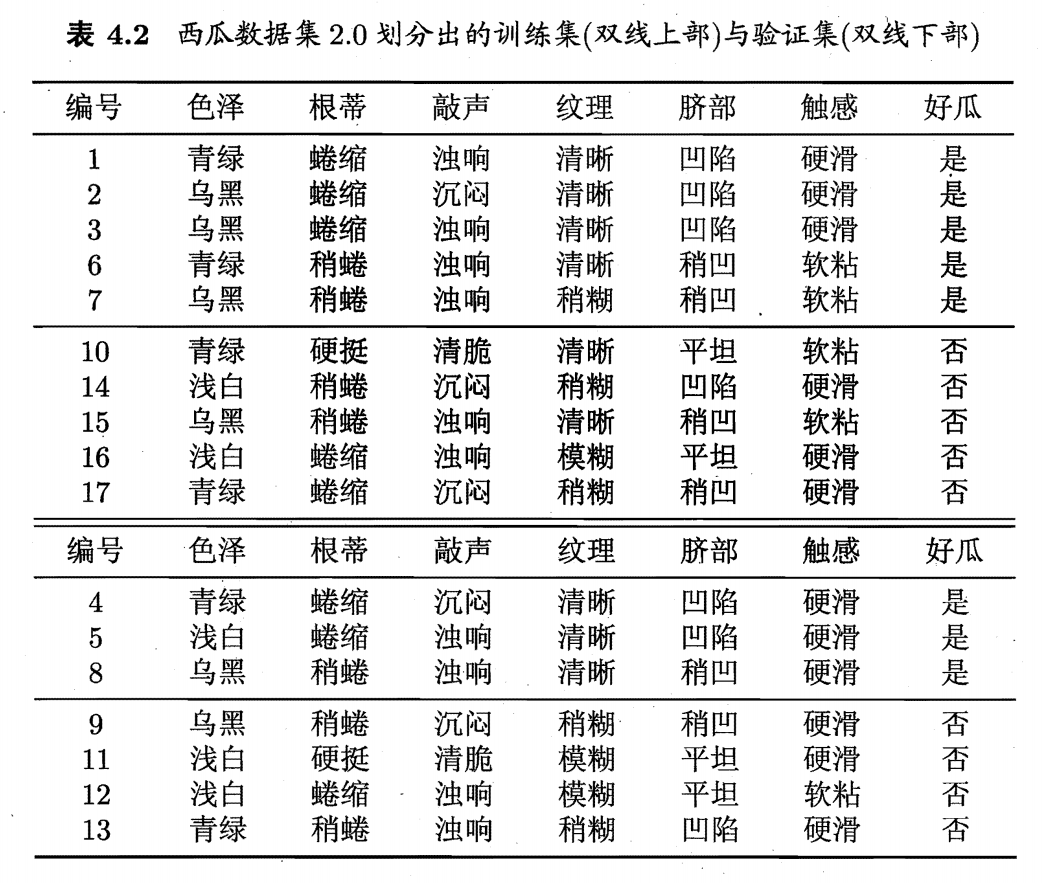
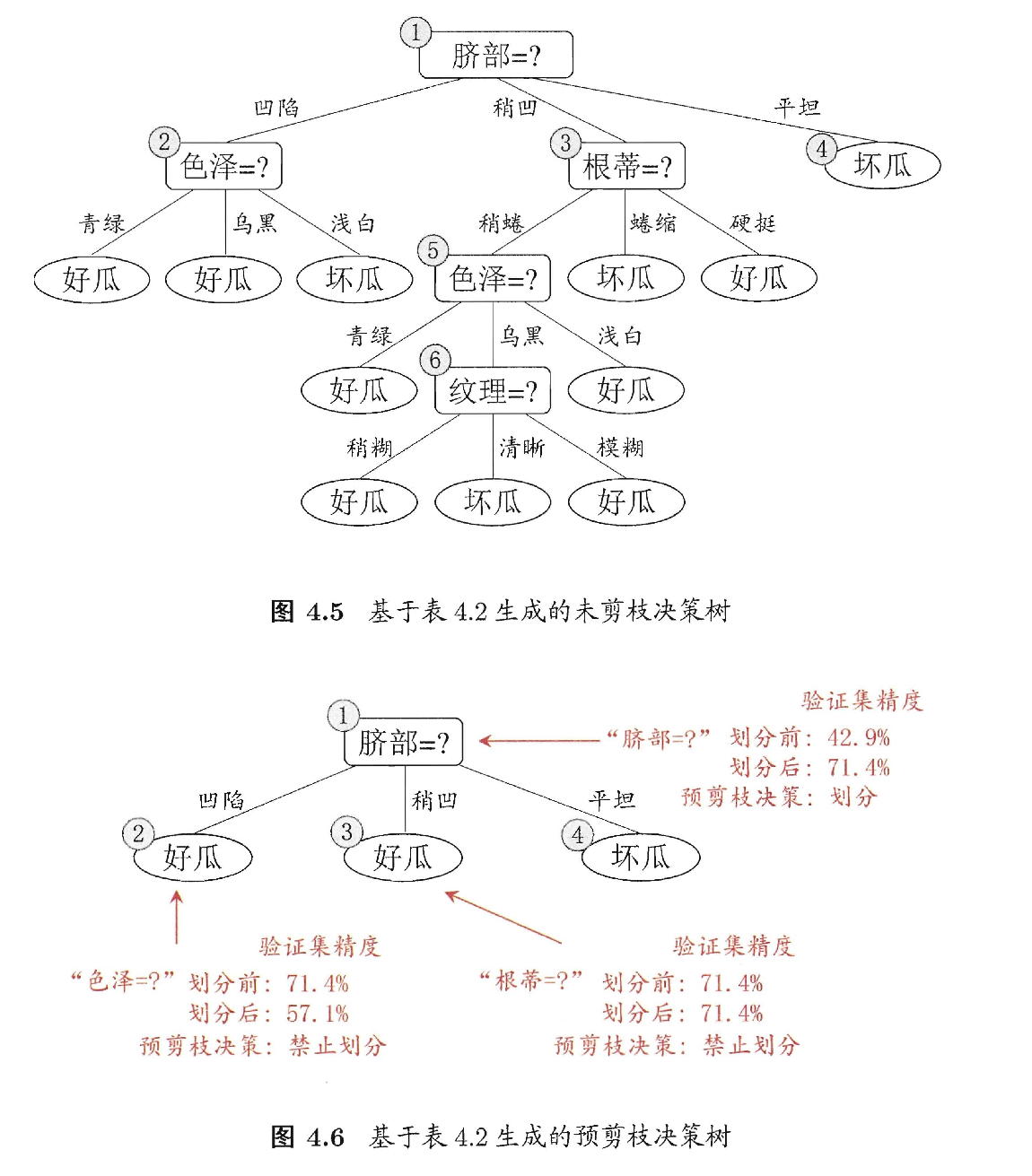
选取属性“脐部”来对训练集进行划分,并产生 3 个分支。假设我们将这个叶节点标记为“好瓜”。用表 4.2 的验证集对这个单结点决策树进行评估,则编号 {4, 5, 8}的样例被分类正确,另外 4 个样例分类错误。验证集精度为
在用属性“脐部”划分之后,图中结点2、3、4分别包含编号 {1, 2, 3, 4}、 {6, 7, 15, 17}、 {10, 16} 的训练样例,分别标记为叶节点“好瓜”、“好瓜”、“坏瓜”。此时,验证集中编号为 {4, 5, 8, 11, 12} 的样例被分类正确,验证集精度为 .于是,“脐部”进行划分得以确定。
后剪枝

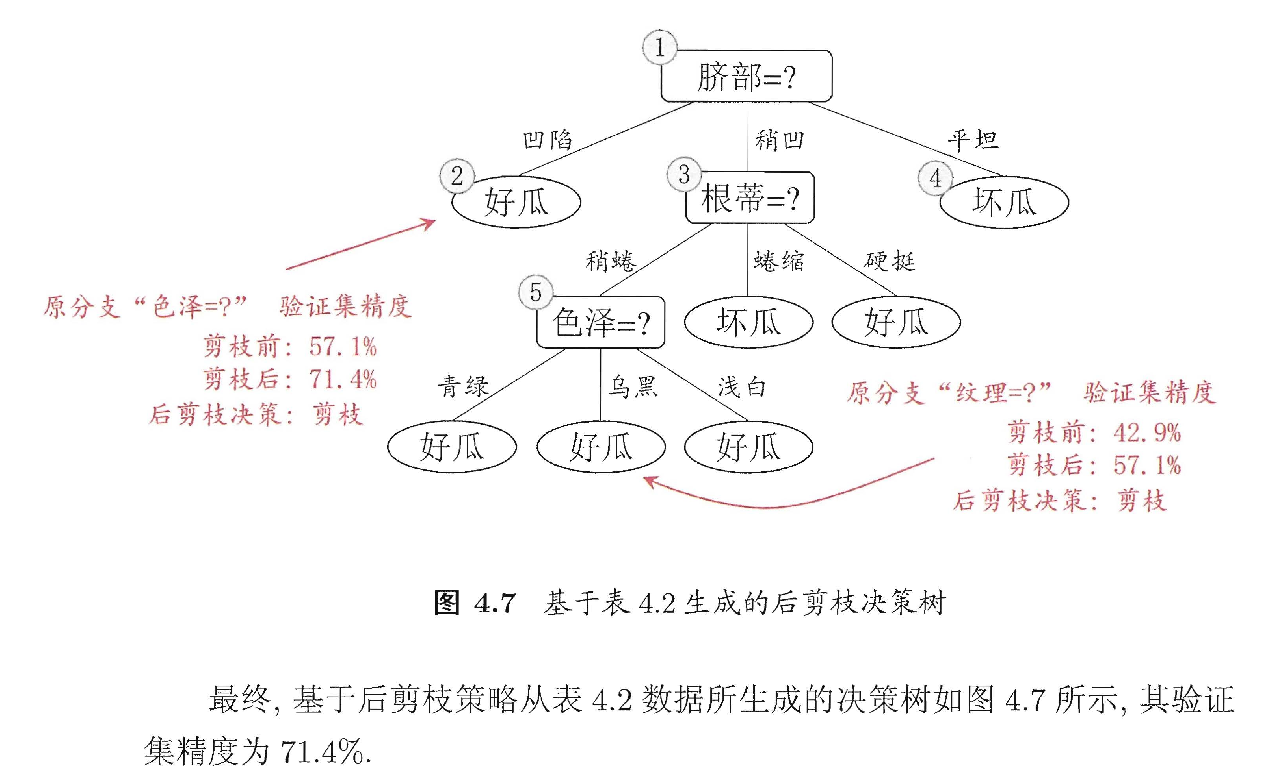
后剪枝决策树通常比预剪枝决策树保留了更多的分支。一般情形,后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树。但后剪枝过程是在生成完全决策树之后进行的,并且要自底向上地对树中所有非叶节点进行逐一考察,因此其训练时间开销要比未剪枝决策树和预剪枝决策树都要大得多