一个有趣的指标定理最近复习复变函数, 发现了一个漂亮的指标定理. 它属于Bernard Malgrange(此人是Lau

最近复习复变函数, 发现了一个漂亮的指标定理. 它属于Bernard Malgrange(此人是Laurent Schwartz的学生). 因为什么都不懂, 不知道这个定理有什么背景, 最多能做到把它解释成"平面区域的Riemann-Roch定理", 所以也就是描述一下罢了, 诸位看官图一乐吧.

参考文献:

GTM 125, p. 624 (我最早查到这个定理的地方)

Malgrange, B., Sur les points singuliers des équations différentielles, Séminaire Équations aux dérivées partielles (Polytechnique) (1971-1972): 1-13. (原始文献)

定理可以表述如下.

设 $\Omega\subset\mathbb{C}$ 是多连通区域, 具有有限的连通数(即第一Betti数) $b _1$ . 考虑全纯函数空间的微分算子 $L:\mathcal{O}(\Omega)\rightarrow\mathcal{O}(\Omega)$ , 定义为

$L=a_n(z)\frac{d^n}{dz^n}+...+a_1(z)\frac{d}{dz}+a_0(z),$

这里诸系数都是 $\Omega$ 上的全纯函数, $a_n$ 在 $\Omega$ 中的零点数目(计算重数) $N$ 为有限. 则 $L$ 是有指标的算子, 且有下列指标公式:

$\mathrm{Ind}(L)=n(1-b_1)-N.$

在这里, 指标的定义与通常一样:

$\mathrm{Ind}(L)=\mathrm{dim}(\mathrm{ker}L)-\dim(\mathrm{coker}L).$

注意 $\mathrm{ker}L$ 指的是定义在整个区域 $\Omega$ 上的 $L$ 的零空间, 因此它的维数 $\leq n$ .

这个定理的证明要分几步.

第一步: 局部的指标定理. 设 $w\in\Omega$ 是 $a_n$ 的一个零点, 取 $r$ 足够小使得 $B(w,r)$ 中没有 $a_n$ 的其它零点. 命 $E_k(w,r)=\mathcal{O}(B(w,r))\cap{C}^k(\bar{B}(w,r))$ , 则熟知它是Banach空间. 易见

$a_{n-1}(z)\frac{d^{n-1}}{dz^{n-1}}+...+a_0(z):E_{n}(w,r)\rightarrow E_0(w,r)$

是紧算子, 从而若计算指标, 只需要计算首项的指标就够了. 据此容易算出

$\mathrm{Ind}(L:E_n(w,r)\rightarrow E_0(w,r))=n-v(a_n,w)$ .

这里 $v(f,w)$ 是全纯函数 $f$ 在 $w$ 点的valuation(零点的阶). 由此再加上一些初等的复变函数知识, 容易过渡到局部的指标定理

$\mathrm{Ind}[L:\mathcal{O}(B(w,r))]=n-v(a_n,w)$ .

第二步: 首项 $a_n$ 没有零点的情形. 设 $\Delta$ 是有限连通区域, 第一个Betti数是 $\beta$ . 在 $\Delta$ 上考虑微分算子 $L:\mathcal{O}(\Delta)\rightarrow\mathcal{O}(\Delta)$ , 定义为

$L=a_n(z)\frac{d^n}{dz^n}+...+a_1(z)\frac{d}{dz}+a_0(z),$

其中 $a_n$ 在 $\Delta$ 上不取零值. 要证明 $\mathrm{Ind}(L)=n(1-\beta).$

根据拓扑知识, 可以造出 $\beta$ 条彼此不相交的Jordan弧 $J_1,...,J_\beta$ , 使得(1)它们的端点都在 $\partial\Delta$ 上(2) $\Delta\setminus J$ 是单连通的区域, 其中 $J=J_1\cup...\cup J_\beta$ . 又可以作出彼此不交的单连通区域 $U_1,...,U_\beta\subset\Delta$ , 使得 $J_k\subset U_k$ 且 $U_k\setminus J_k$ 有两个分支(如图).

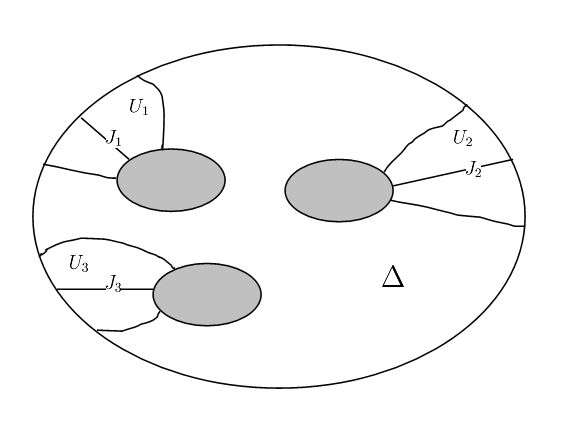
这个时候就需要开始借助一点层论工具了. 容易定义 $\Delta$ 上 $L$ 的零空间层, 它在一点的的stalk是 $L$ 在这一点处的零空间. 于是这是一个复向量空间的层, 每一点的stalk都可以看成全纯函数芽空间的子空间, 具有复维数 $n$ . 记这个层为 $\mathcal{N}$ . 由于微分算子 $L$ 的首项系数没有零点, 根据常微分方程解的局部存在定理, 显然有层的短正合列

$0\rightarrow\mathcal{N}\rightarrow\mathcal{O}\xrightarrow{L}\mathcal{O}\rightarrow0.$

由此导出上同调的长正合列

$0\rightarrow\Gamma(\Delta,\mathcal{N})\rightarrow\Gamma(\Delta,\mathcal{O})\xrightarrow{L}\Gamma(\Delta,\mathcal{O})\rightarrow...$ .

又有下面写出的两个层的短正合列:

$0\rightarrow\mathcal{N}_J\rightarrow\mathcal{N}\rightarrow\mathcal{N}_{\Delta\setminus J}\rightarrow0.$
$0\rightarrow\mathcal{O}_J\rightarrow\mathcal{O}\rightarrow\mathcal{O}_{\Delta\setminus J}\rightarrow0.$

由此导出两个上同调的长正合列

$0\rightarrow\Gamma(J,\mathcal{N})\rightarrow\Gamma(\Delta,\mathcal{N})\rightarrow\Gamma({\Delta\setminus J},\mathcal{N})\rightarrow H^1_J(\Delta,\mathcal{N})\rightarrow...$
$0\rightarrow\Gamma(J,\mathcal{O})\rightarrow\Gamma(\Delta,\mathcal{O})\rightarrow\Gamma({\Delta\setminus J},\mathcal{O})\rightarrow H^1_J(\Delta,\mathcal{O})\rightarrow...$

把这些长正合列拼成一个行列都正合的二维交换图, 然后用一下snake lemma, 并且注意到切除定理给出 $H^1_J(\Delta,\mathcal{N})\cong\bigoplus_{k=1}^\beta H^1_J(U_k,\mathcal{N})$ , 而每一个 $H^1_J(U_k,\mathcal{N})$ 的维数是 $n$ ; 最终得到了指标公式

$\mathrm{Ind}(L)=n(1-\beta).$

第三步: 最终情形. 记 $a_n$ 的零点集为 $Z=\{w_1,...,w_m\}$ , 命第二步中的 $\Delta=\Omega\setminus Z$ . 显然有 $\beta=m+b_1$ . 注意到

$\mathrm{Ind}(L,\mathcal{O}(\Omega))=\mathrm{Ind}(L,\mathcal{O}(\Delta))-\mathrm{Ind}(L,\mathcal{O}(\Delta)/\mathcal{O}(\Omega))$ .

只需要计算 $\mathrm{Ind}(L,\mathcal{O}(\Delta)/\mathcal{O}(\Omega))$ . 现在取 $r$ 充分小, 使得圆盘 $B(w_j,r)$ 彼此不交. 立刻可以看出

$\mathcal{O}(\Delta)/\mathcal{O}(\Omega)\cong\bigoplus_{j=1}^m \mathcal{O}(B'(w_j,r))/\mathcal{O}(B(w_j,r))$ , 其中 $B'(w_j,r)$ 表示去心邻域.

于是算得

$\begin{aligned} \mathrm{Ind}(L,\mathcal{O}(\Omega))&=\mathrm{Ind}(L,\mathcal{O}(\Delta))-\sum_{j=1}^m\{\mathrm{Ind}[L,\mathcal{O}(B'(w_j,r))]-\mathrm{Ind}[L,\mathcal{O}(B(w_j,r))]\}\\ &=n(1-b_1-m)+\sum_{j=1}^m(n-v(a_n,w_j))\\ &=n(1-b_1)-N. \end{aligned}$

这里用到了 $\mathrm{Ind}[L,\mathcal{O}(B'(w_j,r))]=0$ (用第二步的结论即可推出, 因为去心圆盘的第一Betti数是1).