为什么要对数据做中心化和标准化处理？本文作为学习笔记，内容摘抄自网页+自己的感想。如有错误的地方，还望指正。在回归问题

本文作为学习笔记，内容摘抄自网页+自己的感想。如有错误的地方，还望指正。

在回归问题和一些机器学习算法中，以及训练神经网络的过程中，通常需要对原始数据进行中心化（Zero-centered 或者 Mean-subtraction）处理和标准化（Standardization 或者 Normalization）处理。

1.矩阵中心化

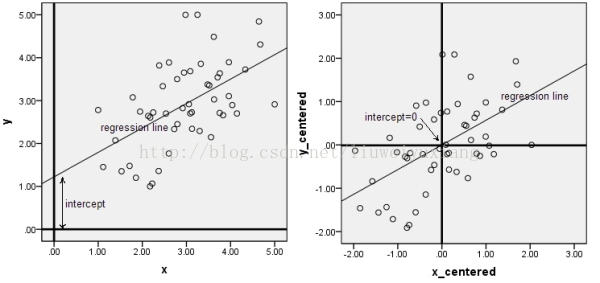
矩阵中心化是使用数据减去数据的均值。 $\mu$ 表示n个数据样本的均值,x_i表示数据样本，则数据中心化使用如下公式计算：x_i^'=(x_i- $\mu$ ),i=1,2,3,...,n。(假定数据样本进行了中心化，即 $\sum\nolimits_i{x_i=0}$ )下面的图是数据做中心化（centering）前后的对比，可以看到其实就是一个平移的过程，平移后所有数据的中心是(0,0)。

2.矩阵标准化

目的：通过对数据进行标准化处理，得到均值为0，标准差为1的服从标准正态分布的数据。（相对一维数据来说，也就是相对矩阵的每一列，数据的每一个维度）
计算过程由下式表示：x'= $\frac{x-\mu}{\sigma}$ ， $\mu$ 表示均值， $\sigma$ 表示标准差，（ $\mu$ 和 $\sigma$ 都可以看成是行向量形式，它们的每个元素分布表示矩阵每一列的均值和方差）可以看出矩阵中心化是标准化的一步，将中心化的矩阵除以标准差得到标准化矩阵。
下面解释一下为什么需要使用这些数据预处理步骤：
在一些实际问题中，我们得到的样本数据都是多个维度的，即一个样本是用多个特征来表示的。比如在预测房价的问题中，影响房价y的因素有房子面积x₁，卧室数量x₂等，我们得到的样本数据就是(x₁,x₂)这样一些样本点，这里的x₁，x₂又被称为特征。很显然，这些特征的量纲和数值的量级都是不一样的（比如房子面积x₁的单位是..m²，80m²，100m²；而卧室数量x₂单位是..间，1间，2间），在预测房价时，如果直接使用原始的数据值，那么它们对房价的影响程度将是不一样的，而通过标准化处理，可以使得不同的特征具有相同的尺度（Scale）。这样，在使用梯度下降法学习参数的时候，不同特征对参数的影响程度就一样了。
简言之，当原始数据不同维度上的特征的尺度（单位）不一致时，需要标准化步骤对数据进行预处理。
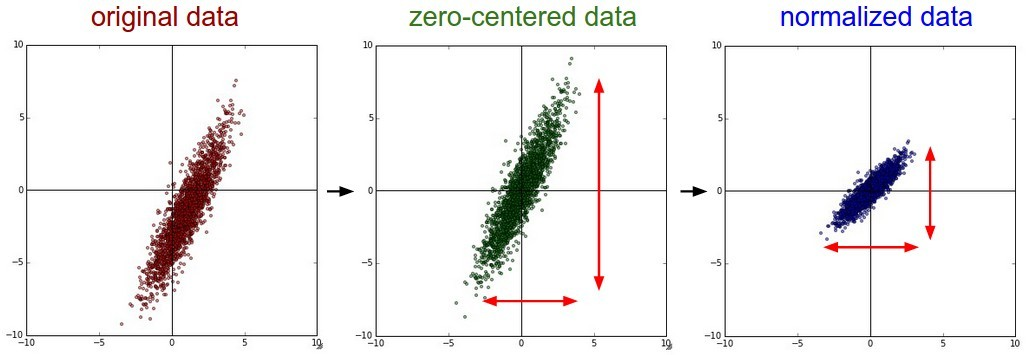
下面中以二维数据为例：左图表示的是原始数据；中间的是中心化后的数据，数据被移动到原点周围；右图将中心化后的数据除以标准差，得到为标准化的数据，可以看出每个维度上的尺度是一致的（红色线段的长度表示尺度）。

其实，在不同的问题中，中心化和标准化有着不同的意义。

比如在训练神经网络的过程中，通过将数据标准化，能够加速权重参数的收敛；
另外，对于主成分分析（PCA）问题，也需要对数据进行中心化和标准化等预处理步骤。

[内容出处]www.zhihu.com/question/37…
blog.csdn.net/liuweiyuxia…