波兰表示法与表达式树昨晚撰写答案《Milo Yip：怎么用 C 语言画出二叉树的图形？》，以 ASCII 字符打印任意深

昨晚撰写答案《Milo Yip：怎么用 C 语言画出二叉树的图形？》，以 ASCII 字符打印任意深度的满二叉树（full binary tree）。评论中问及如何打印非满二叉树。我记起，整个满二叉树可存储在单个一维数组。那么，可以先把非满二叉树的节点写到一维数组，然后修改打印程序，如果数组中存有该序号的节点，才打印该节点及其指向父节点的连线，否则打印空白占位字符。

我的回评或过于简短，不够清晰，因此我想用实际代码解释。然而，怎样建一个非满二叉树？我想到可以写一个简单的表达式解析器，支持加减乘除，不支持负数操作数。程序也能打印出其表达式树。

最简单的表达式语法，莫过于波兰表示法（Polish notation）。波兰表示法又称为前缀表示法，即运算符写在前面。波兰表示法的特点是不需要括号。例如，表达式(1 + 2) * (3 - 4) 的波表示法是 * + 1 2 - 3 4。

（题图 photo by Elliott Engelmann）

首先设计解析后的数据结构，表达式树的节点可能是运算符或操作数：

typedef enum { NUM, ADD, SUB, MUL, DIV } Type;

typedef struct NodeTag {
    union {
        double number;
        struct NodeTag *children[2];
    } u;
    Type type;
} Node;

因为一个节点不会同时为运算符或操作数，采用 union可能节省一点内存。

波兰表示法的解释器非常简单，可通过递归实现，不需要额外的数据结构：

Node* parse(char** s) {
    while (isspace(**s))
        (*s)++;    
    if (**s == '\0')
        return NULL;
    else {
        Node* n = (Node*)calloc(1, sizeof(Node));
        if (isdigit(**s)) {
            n->type = NUM;
            n->u.number = strtod(*s, s);
        }
        else {
            int i;
            switch (**s) {
                case  '+': n->type = ADD; break;
                case  '-': n->type = SUB; break;
                case  '*': n->type = MUL; break;
                case  '/': n->type = DIV; break;
                default: release(n); return NULL;
            }
            (*s)++;
            for (i = 0; i < 2; i++)
                if ((n->u.children[i] = parse(s)) == NULL) {
                    release(n);
                    return NULL;
                }
        }
        return n;
    }
}

每次有内存分配，都匹对释放，也是递归：

void release(Node* n) {
    int i;
    if (n->type != NUM)
        for (i = 0; i < 2; i++)
            if (n->u.children[i])
                release(n->u.children[i]);
    free(n);
}

然后我们可以打印中缀表示法：

#define OPERATOR_CHAR(n) ("+-*/"[n->type - ADD])

void printInfix(const Node *n) {
    if (n->type == NUM)
        printf("%lg", n->u.number);
    else {
        putchar('(');
        printInfix(n->u.children[0]);
        printf(" %c ", OPERATOR_CHAR(n));
        printInfix(n->u.children[1]);
        putchar(')');
    }
}

以及对表达式树求值：

double eval(const Node* n) {
    switch (n->type) {
        case ADD: return eval(n->u.children[0]) + eval(n->u.children[1]);
        case SUB: return eval(n->u.children[0]) - eval(n->u.children[1]);
        case MUL: return eval(n->u.children[0]) * eval(n->u.children[1]);
        case DIV: return eval(n->u.children[0]) / eval(n->u.children[1]);
        case NUM: return n->u.number;
    }
}

编写main()：

int main(int argc, char** argv) {
    if (argc != 2)
        return printf("Help: pntree \"+ * 1 2 3\"");
    else {
        char** p = &argv[1];
        Node* root = parse(p);
        if (root) {
            printInfix(root);
            printf(" = %lg\n", eval(root));
            release(root);
        }
        else
            return printf("Invalid input\n");
    }
}

测试：

$ ./pntree "* + 1 2 - 3 4"
((1 + 2) * (3 - 4)) = -3

接下来，我们要修改之前的满二叉树打印程序。和之前的需求不一样，树的深度是随输入改变的，所以需先求出最大高度（深度）：

int maxDepth(const Node* n) {
    if (n->type == NUM)
        return 1;
    else {
        int maximum = 0, i, d;
        for (i = 0; i < 2; i++)
            if (maximum < (d = maxDepth(n->u.children[i])))
                maximum = d;
        return maximum + 1;
    }
}

接着是分配一个 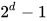2^d-1 大小的数组，把序号映射至节点：

void fillMap(Node** map, Node* n, int index) {
    int i;
    map[index] = n;
    if (n->type != NUM)
        for (i = 0; i < 2; i++)
            fillMap(map, n->u.children[i], index * 2 + i + 1);
}

void printTree(Node* n) {
    int depth = maxDepth(n), i, j, index;
    Node** map = (Node**)calloc((1 << depth) - 1, sizeof(Node*));
    fillMap(map, n, 0);
    // ...
    free(map);
}

这里和原答案一样，使用广度优先遍历去打印节点。先忽略连线的部分：

void putchars(char c, int n) {
    while (n--)
        putchar(c);
}

int printNode(Node* n, int w) {
    if (n->type == NUM)
        return printf("%*lg", w, n->u.number);
    else
        return printf("%*c", w, "+-*/"[n->type - ADD]);
}

void printTree(Node* n) {
    int depth = maxDepth(n), i, j, index;
    Node** map = (Node**)calloc((1 << depth) - 1, sizeof(Node*));
    fillMap(map, n, 0);
    for (j = 0, index = 0; j < depth; j++) {
        int w = 1 << (depth - j + 1);
        // Curve to parent ...
        // Node content
        for (i = 0; i < 1 << j; i++, index++)
            if (map[index])
                putchars(' ', w * 2 - printNode(map[index], w));
            else
                putchars(' ', w * 2);
        putchar('\n');
    }
    free(map);
}

putchars(c, n)连续打印 n 个相同字符。

printNode(n, w) 打印节点的内容（运算符或操作数），打印寛度为w个字符，返回实际打印字符数目。

在 printTree(n)中，采用之前相同的两层循环，在内循环里递增序号index，并获取当前节点map[index]。若该序号没有节点，则打印空白字符。

最终结果：

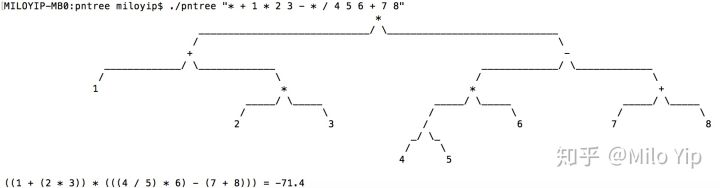
本文简单示范如何实现波兰表示法的计算器，并打印其非满二叉表达式树。此方法需要 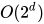O(2^d) 的时间和空间复杂度。如实际节点数量远低于 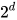2^d ，可考虑用哈希表存储该映射表，但时间复杂度始终无法降低。另一简单优化方法，是用二维数组存储字符输出，那就只需绘画表达式树含有的节点。

完整代码位于 pntree.c。