最近看了看算法，很有意思。算法是构成程序的核心，怎么能不研究研究呢？我想已简单的故事或生活中案例描述这些算法，既希望映像深刻，也更希望大家能够能看明白得以运用。以后学习一个算法，就以自己思路整理发布发布，哈哈φ(>ω<*)

算法来源于生活，在于解决各种问题。我们的一举一动都是经过我们各种思考条件等决定，其中的解决问题的方式方法我觉得既是套路也是算法。

OK,不废话，套路从此开始！

生活

小明是一个山村唯一电工，负责维修电路。昨晚天夜晚，狂风暴雨电闪雷鸣！一段山上50公里长的电线就这样被这场突然来到的风暴弄断了。于是今天，小明于是就需要去维修！小明怎么去知道是哪个部分断了呢？下面是三种方案：

不能乱猜啊！这要是在山上来回乱窜何时是个头！
如果沿着电线走呢？山路陡峭，行动不便，从一头走到另一头50公里得走整整一天，还不包括随时都要观察线路情况。
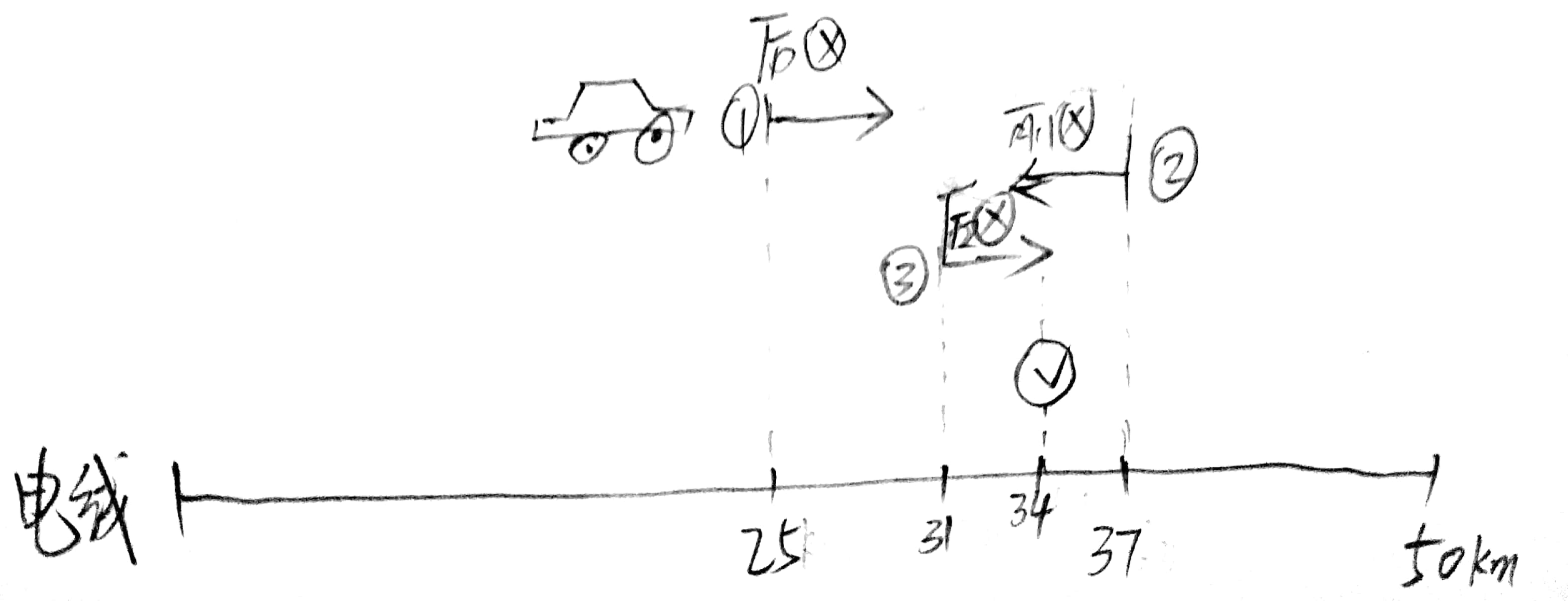
开车直接去线路25公里就是中点处开始测试，如下：
- ①25公里处测试 --> 问题在后半段
- ②37公里处测试 --> 问题在前半段
- ③31公里处测试 --> 问题在前半段
- ④34公里处看到了看到了断掉的线，于是维修

给我选我认为应该选第3种方案，因为这个看起来麻烦测试的次数最少啊！

小明仅仅通过飞跃到这4个地方就能诊断出问题所在，而这使用的方法就是这篇所要说的二分查找。

解决什么？

我们忽略一些细节问题，其实上面的事本身就忽略了很多细节，哈哈。将所有单位去掉50km看做50，下面来看看一些比较。

方案	总数	最多测试次数	次数
方案2	50	50	x
方案2	100000	1000000	x
方案3	50	6	log₂x
方案3	100000	17	log₂x

方案3，二分法，如上面的图，第①次排除一半，第②次又排除一半...。这样最多次数为总次数的对数，很显然二分法在随数量的增加，最多次数却远小于了普通的排查法。
假如测试的数就是第一个呢？那么普通挨着排查，第一次就能查到。而二分法却多做了很多判断。只能说从平均上来说，二分法是查找效率是远大于普通排查。
很显然，对于我们要找一个值的位置，通过二分法是很好的选择。

限制

相信大家也注意到了，对于上面的排查判断的基础，是由于数是连续的，而不是乱序的。
如果数是乱序的则无法进行二分法，因为它是基于有序为基础。

代码

通过传入数组，和需要测试的值，返回在数组中的下标位置

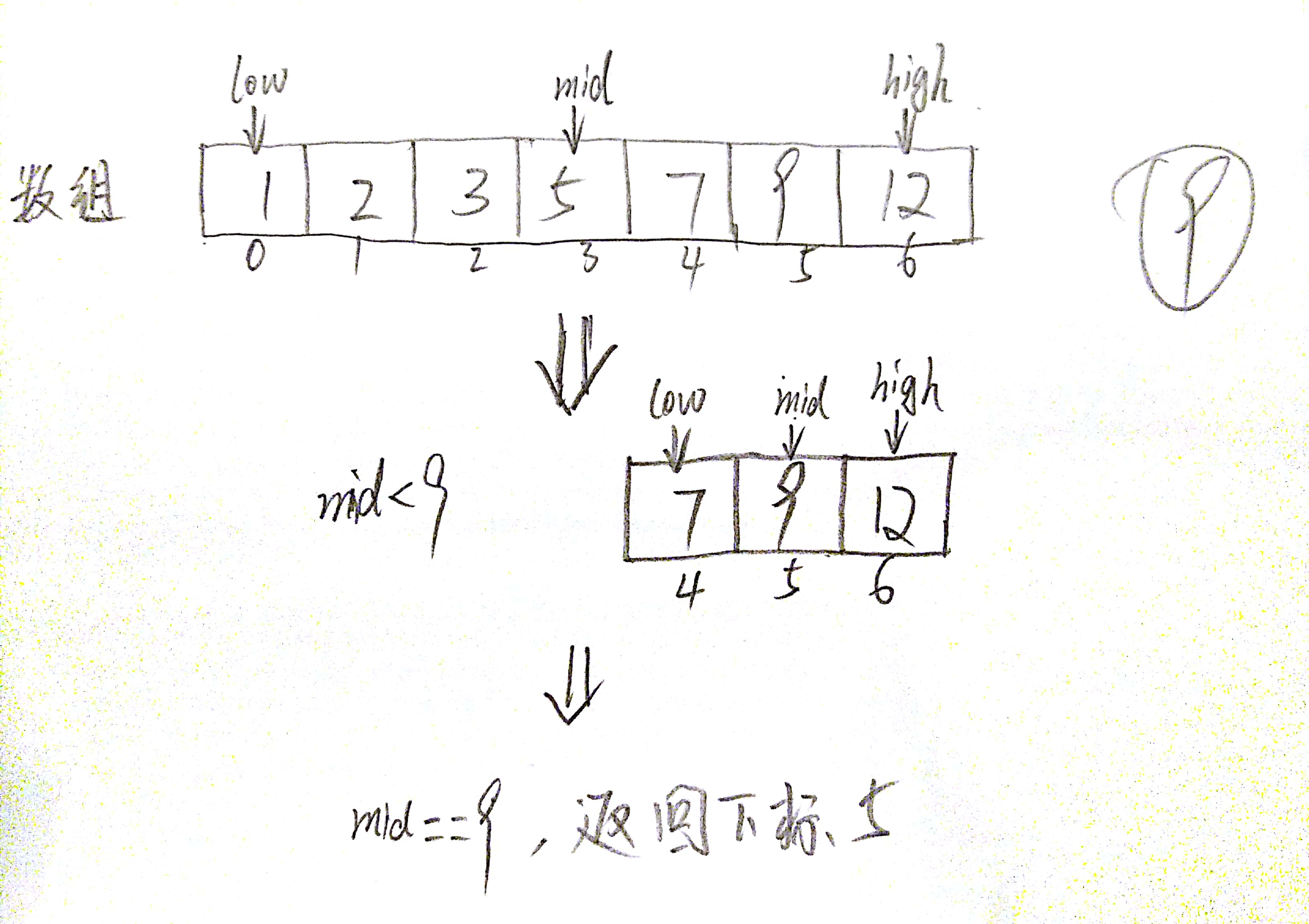
python 代码实现

def binary_search(list, item):
    low = 0 #low和high用于跟踪列表的需要查找部分
    high = len(list) - 1
    while low <= high: # 只要范围缩小到没有一个元素，则跳出循环
        mid = (low + high) // 2 # 每次检查中间的元素
        guess = list[mid]
        if guess == item: # 找对了
            return mid
        elif guess > item: # 数字大了
            high = mid - 1
        else: # 数字小了
            low = mid + 1
    return None # 没找到

my_list = [1, 2, 3, 5, 7, 9]
print(binary_search(my_list, 7))
print(binary_search(my_list, -1))

java 代码实现

public class BinarySearch
{
    public static int search(int[] arr, int item)
    {
        int low = 0;   //low和high用于跟踪列表的需要查找部分
        int high = arr.length;
        while (low <= high)   //只要范围缩小到没有一个元素，则跳出循环
        {
            int mid = (low + high) / 2;   //每次检查中间的元素
            if (arr[mid] == item)   //找对了
            {
                return mid;
            } else if (arr[mid] > item)   //数字大了
            {
                high = mid - 1; 
            } else   //数字小了
            {
                low = mid + 1;
            }
        }
        return -1;  //没找到
    }

    public static void main(String[] args)
    {
        int[] arr = {1, 2, 3, 5, 7, 9};
        System.out.println(search(arr,  3));
        System.out.println(search(arr, -1));
    }
}

总结

这个算法还算简单，上面其实我也搬了一下代码用用。
有个算法的运行时间叫“大O时间”，二分法的时间是O(log₂n)，普通查找时间是O(n)。去百度吧！emmmmm！还是下次总结一下吧！
如果喜欢，可以看看算法图解，将的很清晰，有兴趣的朋友推荐看看。我就想着自己换个花样总结总结，换汤没换药。接下来，我准备明白一个算法，就写一写，练一练，分享分享！
讲的不好，求放过（づ￣3￣）づ╭❤～

算法试刀-二分法查找

生活

解决什么？

限制

代码

总结