(第一部分 机器学习基础)
第1章 机器学习概览
第2章 一个完整的机器学习项目
本章中,你会假装作为被一家地产公司刚刚雇佣的数据科学家,完整地学习一个案例项目。下面是主要步骤:
- 项目概述。
- 获取数据。
- 发现并可视化数据,发现规律。
- 为机器学习算法准备数据。
- 选择模型,进行训练。
- 微调模型。
- 给出解决方案。
- 部署、监控、维护系统。
使用真实数据
学习机器学习时,最好使用真实数据,而不是人工数据集。幸运的是,有上千个开源数据集可以进行选择,涵盖多个领域。以下是一些可以查找的数据的地方:
-
流行的开源数据仓库:
UC Irvine Machine Learning Repository
Kaggle datasets
Amazon’s AWS datasets -
准入口(提供开源数据列表)
dataportals.org/
opendatamonitor.eu/
quandl.com/
- 其它列出流行开源数据仓库的网页:
Wikipedia’s list of Machine Learning datasets
Quora.com question
Datasets subreddit
本章,我们选择的是StatLib的加州房产价格数据集(见图2-1)。这个数据集时基于1990年加州普查的数据。数据已经有点老(1990年还能买一个湾区不错的房子),但是它有许多优点,利于学习,所以假设这个数据为最近的。为了便于教学,我们添加了一个分类属性,并除去了一些。
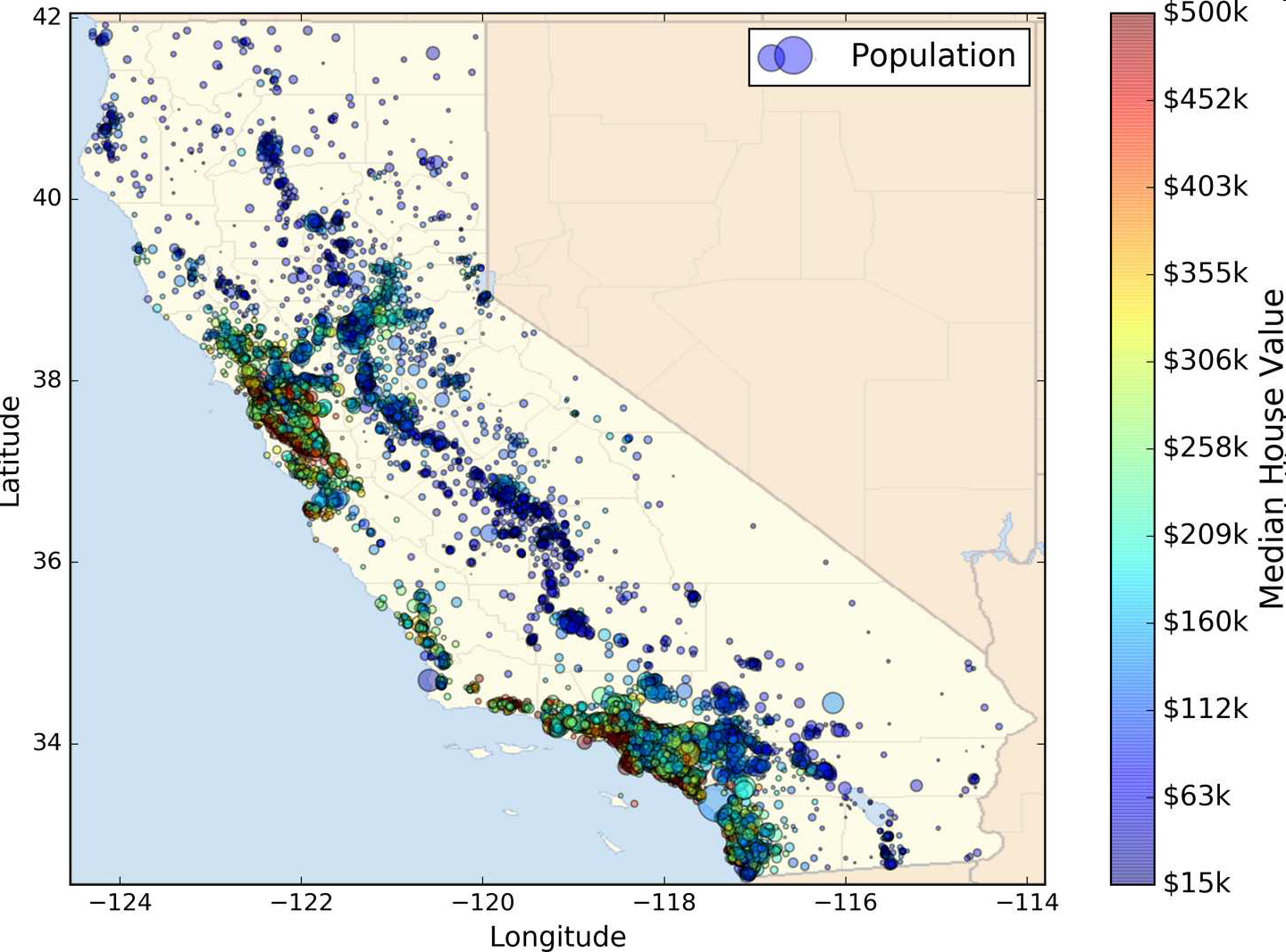 图2-1 加州房产价格
图2-1 加州房产价格
项目概览
欢迎来到机器学习房地产公司!你的第一个任务是利用加州普查数据,建立一个加州房价模型。这个数据包含每个分区组的人口、收入中位数、房价中位数等指标。
分区组是美国调查局发布样本数据的最小地理单位(一个分区通常有600到3000人)。我们将其简称为“分区”。
你的模型要利用这个数据进行学习,然后根据其它指标,预测任何分区的的房价中位数。
提示:你是一个有条理的数据科学家,你要做的第一件事是拿出你的机器学习项目清单。你可以使用附录B中的清单;这个清单适用于大多数的机器学习项目,但是你还是要确认它是否满足需求。在本章中,我们会检查许多清单上的项目,但是也会跳过一些简单的,有些会在后面的章节再讨论。
划定问题
问老板的第一个问题应该是商业目标是什么?建立模型可能不是最终目标。公司要如何使用、并从模型受益?这非常虫咬,因为它决定了如何划定问题,要选择什么算法,评估模型性能的指标是什么,要花多少精力进行微调。
老板告诉你你的模型的输出(一个区的房价中位数)会传给另一个机器学习系统(见图2-2),也有其它信号会传入后面的系统。这一整套系统可以确定某个区进行投资值不值。确定值不值得投资非常重要,它直接影响利润。
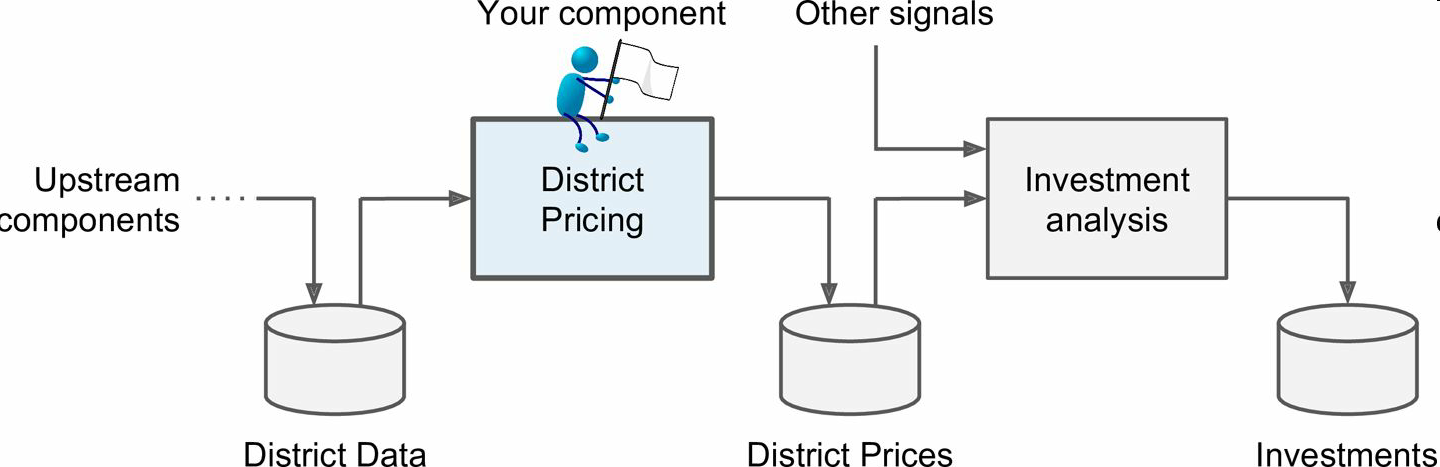 图2-2 房地产投资的机器学习管道
图2-2 房地产投资的机器学习管道
管道 一系列的数据处理组件被称为数据管道。管道在机器学习系统中很常见,因为有许多数据要处理和转换。
组件通常是异步运行的。每个组件吸纳进大量数据,进行处理,然后将数据传输到另一个数据容器中,而后管道中的另一个组件收入这个数据,然后输出,这个过程依次进行下去。每个组件都是独立的:组件间的接口只是数据容器。这样可以让系统更便于理解(记住数据流的图),不同的项目组可以关注于不同的组件。进而,如果一个组件失效了,下游的组件使用失效组件最后生产的数据,通常可以正常运行(一段时间)。这样就使整个架构相当健壮。
另一方面,如果没有监控,失效的组件会在不被注意的情况下运行一段时间。数据会受到污染,整个系统的性能就会下降。
下一个要问的问题是,现在的解决方案效果如何。老板通常会给一个参考性能,以及如何解决问题。老板说,现在分区的放假是靠专家手工估计的,专家队伍手机最新的关于一个区的信息(不包括房价中位数),他们使用复杂的规则进行估计。这种方法费钱费时间,而且估计结果不理想,误差率大概有15%。
Okay,有了这些信息,你就可以开始设计系统了。首先,你需要划定问题:监督或非监督,还是强化学习?这是个分类任务、回归任务,还是其它的?要使用批量学习还是线上学习?继续阅读之前,请暂停一下,尝试自己回答下这些问题。
你能回答出来吗?一起看下答案:很明显,这是一个典型的监督学习任务,因为你要使用的是有标签的训练样本(每个实例都有预定的产出,即分区的房价中位数)。并且,这是一个典型的回归任务,因为你要预测一个值。讲的更细些,这是一个多变量回归问题,因为系统要使用多个变量进行预测(要使用分区的人口,收入中位数等等)。在第一章中,你只是根据人均GDP来预测生活满意度,因此这是一个单变量回归问题。最后,没有连续的数据流进入系统,没有特别需求需要对数据变动作出快速适应。数据量不大可以放到内存中,因此批量学习就够了。
提示:如果数据量很大,你可以要么在多个服务器上对批量学习做拆分(使用MapReduce技术,后面会看到),或是使用线上学习。
选择性能指标
下一步是选择性能指标。回归问题的典型指标是均方根误差(RMSE)。均方根误差测量的是系统预测误差的标准差。例如,RMSE等于50000,意味着,68%的系统预测值位于实际值的$50000以内,95%的预测值位于实际值的$100000以内。等式2-1展示了计算RMSE的方法。
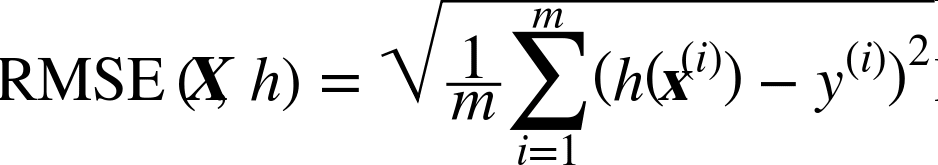 等式2-1 均方根误差(RMSE)
等式2-1 均方根误差(RMSE)
符号的含义
这个方程引入了一些常见的贯穿本书的机器学习符号:
- m是测量RMSE的数据集中的实例数量。
例如,如果用一个含有2000个分区的验证集求RMSE,则m = 2000。- x(i)是数据集第ith个实例的所有特征值(不包含标签)得矢量,y(i)是它的标签(这个实例的输出值)。
例如,如果数据集中的第一个分区位于经度–118.29°,纬度33.91°,有1416名居民,收入中位数是$38372,房价中位数是$156400(不考虑其它特征),则有:
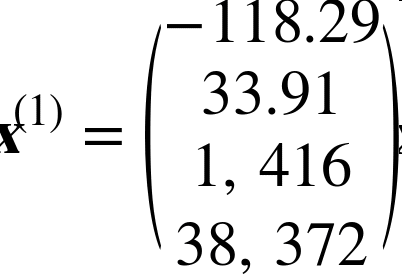
和,
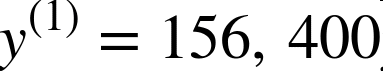
- X是包含数据集中所有实例的所有特征值(不包含标签)的矩阵。每一行是一个实例,第ith行是x(i)的转置,标记为(x(i))T。
例如,仍然是前面的第一区,矩阵X就是:

- h是系统的预测函数,也称为假设(hypothesis)。当系统收到一个实例的特征矢量x(i),就会输出这个实例的一个预测值ŷ(i) = h(x(i))(ŷ读作y-hat)。
例如,如果系统预测第一区的房价中位数是$158400,则ŷ(1) = h(x(1)) = 158400。预测误差是ŷ(1) – y(1) = 2000。
RMSE(X,h)是使用假设h在样本集上测量的损失函数。我们使用小写斜体表示标量值(例如m或y(1))和函数名(例如h),小写粗体表示矢量(例如x(i)),大写粗体表示矩阵(例如X)。(译者注:MarkDown表示粗体斜体太麻烦了,忽略字体。)
虽然大多数时候RMSE是回归任务可靠的性能指标,在有些情况下,你可能需要另外的函数。例如,假设存在许多异常的分区。此时,你可能需要使用绝对平均误差(Mean Absolute Error,也称作平均绝对偏差,见等式2-2):
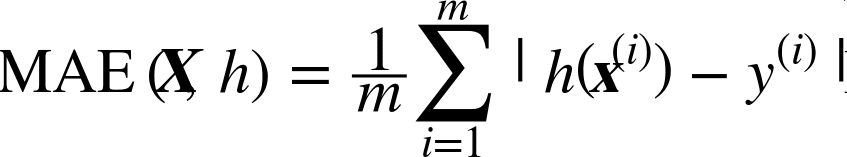 等式 绝对平均误差
等式 绝对平均误差
RMSE和MAE都是测量预测值和目标值两个矢量距离的方法。有多种测量距离的方法,或范数:
-
计算对应欧几里得范数的平方和的根(RMSE):这个距离介绍过。它也称作ℓ2范数,标记为// · //2(或只是// · //)。
-
计算对应于ℓ1(标记为// · //1)范数的绝对值和(MAE)。有时,也称其为曼哈顿范数,因为它测量了城市中的两点,沿着矩形的边行走的距离。
-
更一般的,包含n个元素的矢量v的ℓk范数,定义成

ℓ0只显示了这个矢量的基数(即,元素的个数),ℓ∞是矢量中最大的绝对值。 -
范数的指数越高,就越关注大的值而忽略小的值。这就是为什么RMSE比MAE对异常值更敏感。但是当异常值是指数分布的(类似正态曲线),RMSE就会表现很好。