五、马尔科夫随机场
原文：Markov random fields
译者：飞龙
协议：CC BY-NC-SA 4.0
自豪地采用谷歌翻译
贝叶斯网络是一类模型，可以紧凑地表示许多有趣的概率分布。 但是，我们在前一章已经看到，一些分布不能完全用贝叶斯网络来表示。
在这种情况下，除非我们想在我们的模型的变量之间引入错误的独立性，否则我们必须回到不太紧凑的表示形式（可以将其视为带有不必要的额外边的图）。 这产生了模型中不必要的额外参数，并且使得学习这些参数和做出预测更加困难。
然而，存在另一种技术，用于紧凑地表示和可视化基于无向图的语言的概率分布。 这类模型（称为马尔科夫随机场或 MRF）可以紧凑地表示有向图模型无法表示的分布。 我们将在本章中探讨这些方法的优点和缺点。
马尔科夫随机场
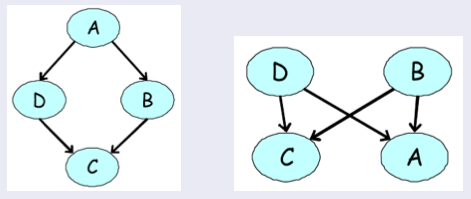
作为一个启发示例，假设我们正在建模A, B, C, D人的投票偏好。 假设(A,B), (B,C), (C,D)和(D,A)是朋友，朋友往往有类似的投票偏好。 这些影响可以自然地由一个无向图表示。
定义A,B,C,D的联合投票决策的概率的一种方法是，将分数赋给这些变量的每个赋值，然后将概率定义为标准化分数。 分数可以是任何函数，但在我们的例子中，我们将其定义为这种形式：
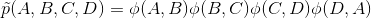
其中ϕ(X,Y)是因子，如果对朋友X, Y的投票一致，它赋予更多权重，例如：
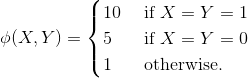
非标准化分布中的因子通常被称为因子。 最终的概率定义为：
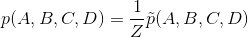
其中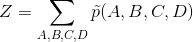 
是标准化常数，确保整个分布和为一。
当标准化时，我们可以将ϕ(A,B)视为一种交互，推动B的投票更接近A的投票。ϕ(B,C)项推动B的投票更靠近C，最可能的投票将需要协调这些冲突影响。
请注意，与有向情况不同，我们没有说明如何从另一组变量生成一个变量（如条件概率分布所做的那样）。 我们只是指出图中非独立变量之间的耦合程度。 从某种意义上说，这需要较少的先验知识，因为我们不再需要讲一个完整的生成性故事，说明B的投票是如何从A的投票中构建出来的（如果我们有P(B|A)因子，就需要这样）。 相反，我们只需确定非独立变量，并定义它们相互作用的强度；这又定义了可能的赋值空间上的能量格局，并且我们通过标准化常数将此能量转换为概率。
形式定义
马尔科夫随机场（MRF）是由变量x1, ..., xn组成的概率分布p，由无向图G定义，其中节点对应于变量xi。 概率p形式为：
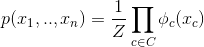
其中C表示G的团集合（即完全连通子图）。
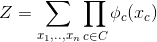
是标准化常数，确保整个分布和为一。
因此，给定图G，我们的概率分布可能包含一些因子，它的范围是G中的任何团，可以是单个节点，边，三角形等。注意，我们不需要为每个团指定因子。 在我们上面的例子中，我们在每个边上定义了一个因子（这是两个节点的团）。 但是，我们选择不指定任何单一因子，即单个节点上的团。
与贝叶斯网络比较
用于我们的四变量投票示例的有向模型示例。 他们都不能准确地表达，我们的变量之间依赖结构的先验知识。
在我们之前的投票例子中，A, B, C, D的分布满足A⊥C|{B,D}和B⊥D|{A,C}（因为一个人的投票只受朋友直接影响）。 我们可以很容易地通过反例来检查，这些独立性不能完全由贝叶斯网络表示。 然而，MRF 结果是这个分布的完美映射。
更一般地说，MRF 与有向模型相比有几个优点：
- 它们可以应用于更广泛的问题，其中没有和变量依赖相关的天然方向性。
- 无向图可以简洁地表达某些依赖关系，贝叶斯网络不容易描述它们（尽管反过来也是如此）。
它们也有几个重要的缺点：
- 计算归一化常数
Z需要对可能为指数数量的赋值进行求和。 在一般情况下，我们会看到这将是 NP 难的；因此许多无向模型是棘手的并需要近似技术。 - 无向模型可能难以解释。
- 从贝叶斯网络生成数据要容易得多，这在某些应用中很重要。
不难看出，贝叶斯网络是 MRF 的特例，带有非常特定类型的团聚因子（对应于条件概率分布并且暗示图中的有向非循环结构）和归一化常数 1。 特别是，如果我们取一个有向图G，并向给定节点的所有父节点添加侧边（并消除它们的方向性），那么CPD（看做变量及其祖先的因子）可以在生成的无向图上因式分解。 由此产生的过程被称为规范化（Moralization）。
贝叶斯网络总是可以转换成标准化常数为 1 的无向网络。 反过来也是可能的，但是可能在计算上难以处理，并且可能产生非常大的（例如全连通的）有向图。
因此，MRF 比贝叶斯网络具有更多的功能，但更难以计算处理。 一般的经验法则是，尽可能使用贝叶斯网络，如果没有使用有向图对问题进行建模的自然方式（例如我们的投票示例），只能切换为 MRF。
MRF 中的独立性
回想一下，在贝叶斯网络的情况下，我们定义了由有向图G描述的一组独立性I(G)，并展示了它们如何描述必须在分布p中保持的真正独立性，分布p在有向图上因式分解，也就是I(G)⊆I(p)。
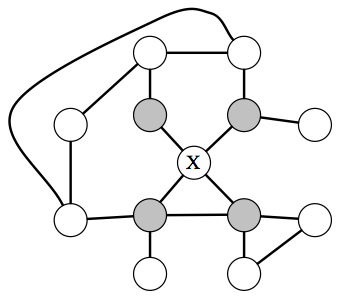
在 MRF 中，以所有邻居为条件，节点X独立于图的其余部分（称为X的马尔可夫毯）。
那么可以通过无向 MRF 描述哪些独立性？ 这里的答案非常简单直观：如果变量x，y由未观测变量的路径连接，则它们是相关的。 但是，如果x的邻居都被观察到，那么x与所有其他变量无关，因为它们只能通过它的邻居影响x。
特别是，如果一组观察变量在图的两半之间形成一个切集，则一半的变量与另一半的变量无关。
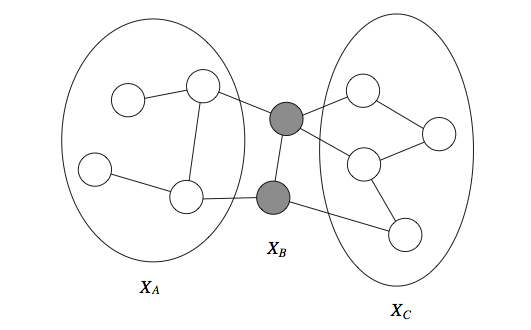
形式上，我们将变量X的马尔可夫覆盖集U定义为节点的最小集合，满足如果观察到U，X与图的其余部分无关，即X⊥(X−{X}−U)|U。 这个概念适用于有向和无向模型，但在无向情况下，马尔可夫毯变成仅仅是节点的邻居。
在有向的情况下，我们发现I(G)⊆I(p)，但是存在分布p，其独立性不能用G来描述。在无向情况下，同样的情况也成立。 例如，考虑由有向v结构描述的概率（即 explaining away 现象）。 无向模型不能描述独立性假设X⊥Y。
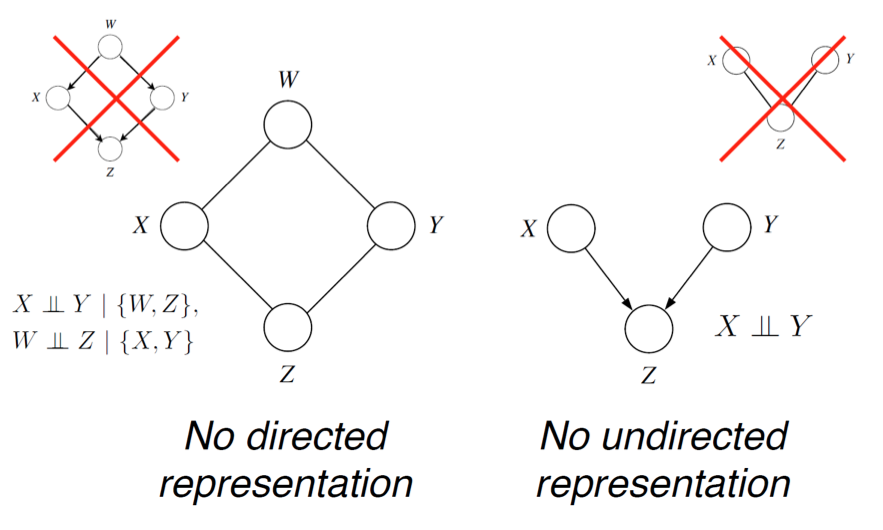
具有完美的有向图表示，但没有无向表示的概率分布示例，以及反例。
条件随机场
当马尔可夫随机场用于模拟条件概率分布p(y|x)时，它们的一个重要特例就产生了。 在这种情况下，x∈X和y∈Y是向量值变量; 我们通常以x为条件，并且希望说一些y的有趣的东西。 通常情况下，这种分布将出现在监督式学习设定中，其中y将是我们试图预测的向量值标签。 这个设定通常称为结构化预测。
示例
作为一个启发示例，考虑从字符图像序列xi∈[0,1] d×d中识别单词的问题，它以像素矩阵形式提供给我们。 我们的预测器的输出将是一系列字母yi∈{'a', 'b', ..., 'z'}。
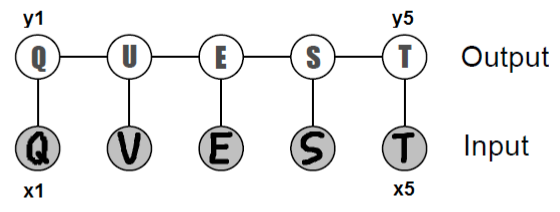
用于光学字符识别的链式结构的条件随机场。
我们原则上可以训练一个分类器，从它的xi中分别预测每个yi。 然而，由于这些字母组合在一起形成一个词，所以跨越不同i的预测应该互相知道。 在上面的例子中，第二个字母本身可以是'U'或'V'；然而，由于我们可以高度自信地判断其邻居是'Q'和'E'，我们可以推断'U'是最可能的真实标签。
CRF 将成为一个工具，使我们能够联合执行这个预测。
形式定义
形式上，CRF 是个变量X∪Y上的马尔科夫网络，规定了条件分布：
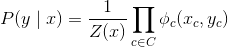
分区函数为：
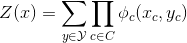
请注意，在这种情况下，分区常量现在取决于x（因此，我们说它是一个函数），这并不令人惊讶：p(y|x)是由x参数化的y的概率，即对于每个x，它编码 了不同的概率函数。 在这个意义上，对于每个输入x，条件随机场产生了新的马尔可夫随机场的实例。
示例（续）
更正式地说，假设p(y|x)是一个链式 CRF，具有两种类型的因子：i = 1, ..., n的图像因子ϕ(xi,yi)，它赋予与xi一致的yi更高的值 - 以及i = 1, ..., n-1的成对因子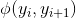 
。 我们也可以将ϕ(xi,yi)看作概率p(yi|xi)，由标准（非结构化）softmax 回归提供；可以将 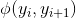看作字母的经验频率，它们从大量英文文本（例如维基百科）中获得。
在这个形式的模型的条件下，我们可以使用 MAP 推断，联合推断结构化标签y。
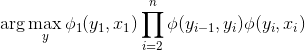
CRF 特征
在多数实际应用中，我们进一步假设，因子ϕc(xc,yc)形式为：
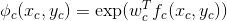
其中fc(xc,yc)可以是描述xc和yc之间兼容性的任意一组特征。
在我们的 OCR 例子中，我们可以引入特征f(xi,yi)；它编码字母yi与像素xi的兼容性。 例如，f(xi,yi) 可能是字母yi的概率，由逻辑回归（或深度神经网络）评估像素xi而产生。 另外，我们在相邻字母之间引入了特征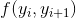 
。 它们可以是 
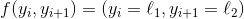形式的指标，其中l1，l2是字母表中的两个字母。 然后，CRF 将学习权重w，它将为连续字母(l1,l2)的更常见的概率赋予更多的权重，同时确保预测的yi与输入xi一致;
这个过程会让我们在xi不明确的情况下确定yi，就像我们上面的例子一样。
需要对 CRF 特征做出最重要的认识是，它们可以任意复杂。 事实上，我们可以定义一个 OCR 模型，其因子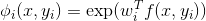 
，这取决于整个输入x。 这完全不会影响计算性能，因为在推断时间内，x总会被观察到，而我们的解码问题将涉及到最大化：
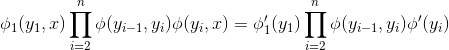
其中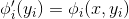 
。使用全局特征只会改变因子的值，但不会改变它们的范围，它们具有相同类型的链结构。我们将在下一节中看到，这种结构是所需的，确保我们可以轻松解决这个优化问题。
x，y上的单一模型，归一化常数为
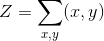）来建模p(x,y)，那么我们需要将两个分布拟合为数据：p(y|x)和p(x)。然而，如果我们感兴趣的是给定x预测y，那么p(x)的建模是不必要的。事实上，这样做统计上可能是不利的（例如，我们可能没有足够的数据来拟合p(y|x)和p(x)；因为模型具有公共参数，所以拟合一个可能产生另一个的最佳参数），它可能在计算上不是好主意（我们需要做出分布中的简化假设，以便容易地处理p(x)）。
CRF 放弃了这个假设，并且往往在预测任务上表现更好。
