在上个视频里,我们学习了 logistic 回归模型,也知道了损失函数。损失函数衡量单一训练样例的效果。你还知道了成本函数,用于衡量参数w和b的效果,在全部训练集上来衡量。
下面我们讨论如何使用梯度下降法,来训练或学习训练集上的参数w和b。回顾一下,这里是熟悉的 logistic 回归算法。第二行是成本函数J,成本函数J是参数w和b的函数。它被定义为平均值,即1/m的损失函数之和。损失函数可以衡量你的算法的效果,对每一个训练样例都输出y_hat^(i),把它和与基本真值标签y^(i)进行比较。完整的公式在等号右边展开。成本函数衡量了参数w和b在训练集上的效果。
要习得合适的参数w和b,很自然地就想到,我们想找到使得成本函数J(w, b)尽可能小的w和b。下面来看看梯度下降法,这个图中的横轴表示空间参数w和b,在实践中w可以是更高维的。但为了方便绘图,我们让w是一个实数,b也是一个实数,成本函数J(w,b)是在水平轴w和b上的曲面。曲面的高度表示了J(w,b)在某一点的值。
我们所想要做的就是,找到这样的w和b,使其对应的成本函数J值是最小值。可以看到成本函数J是一个凸函数,像这样的一个大碗。因此,这是一个凸函数,看起来和这样的函数不一样,它是非凸的,有很多不同的局部最优。
因此我们的成本函数J(w,b)定义为凸函数,是我们将这个特定成本函数J用于 logistic 回归的的重要原因之一。为了找到更好的参数值,我们要做的就是,用某初始值初始化w和b,用那个小红点表示。对于 logistic 回归而言,几乎是任意的初始化方法都有效。通常用0来进行初始化,随机初始化也有效。
但是对于 logistic 回归,我们通常不这么做,但因为函数是凸的,无论在哪里初始化,都应该达到同一点,或大致相同的点。梯度下降法所做的就是,从初始点开始,朝最陡的下坡方向走一步。在梯度下降一步后,或许在那里停下,因为它正试图沿着最快下降的方向往下走,或者说尽可能快地往下走。
这是梯度下降的一次迭代,两次迭代或许会到达那里,或者三次……等等。我估计它隐藏在图上的曲线中,很有希望收敛到这个全局最优解,或接近全局最优解。这张图片阐述了梯度下降法,我们多写一点细节,为了更好地说明,让我们来看一些函数。
你希望得到最小化J(w),函数可能会看起来像这样,为了方便画我先忽略b,仅仅是用一维曲线,来代替多维曲线。梯度下降法是这样做的,我们将重复执行以下的更新操作,我们更新w的值,使用:=表示更新,让w为w - α * dJ(w)/dw。在算法收敛之前我会重复这样去做。
我要说明公式中的两点,这里的α表示学习率,学习率可以控制每一次迭代,或者梯度下降法中的步长。我们之后会讨论如何选择学习率α。其次在这里的这个数是导数,这就是对参数w的更新或者变化量。当我们开始编写代码,来实现梯度下降,我们会使用代码中变量名的约定。dw表示导数,像这样编写代码,即w:=w - α * dw。我们用dw作为导数的变量名。
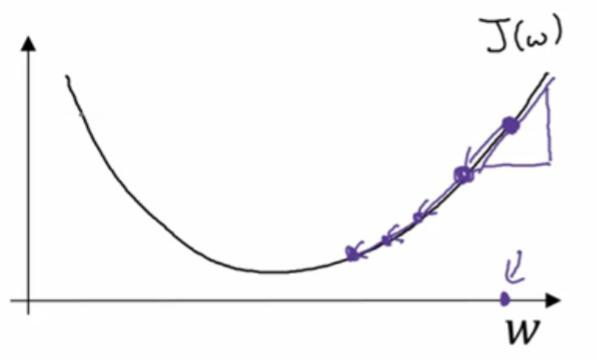
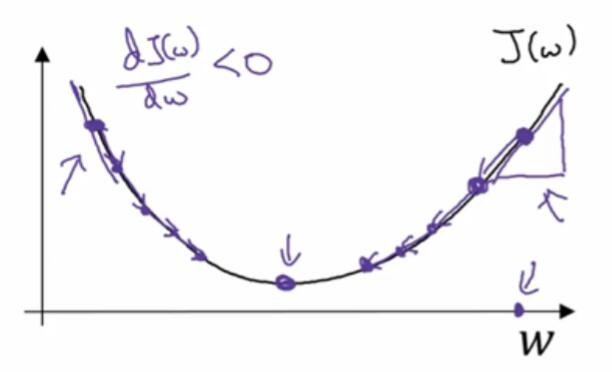
现在我们确保梯度下降法更新是有用的,w在这,对应的成本函数J(w)在曲线上的这一点。记住导数的定义,是函数在这个点的斜率,而函数的斜率是高除以宽,在这个点相切于J(w)的一个小三角形。在这里导数是正,新的w值等于w自身减去学习率乘导数。导数是正的,从w中减去这个乘积,就向左边走一步。对于一开始就很大的参数w来说,像这样,梯度下降法让你的算法,渐渐地减小这个参数w。
另一个例子,如果w的位置是在这里,这个点处的斜率将会是负的。用梯度下降法去更新,w将会减去α乘上一个负数,慢慢使得参数w增加。不断地用梯度下降法来迭代,w会变得越来越大。无论你初始化的位置,是在左边还是右边,梯度下降法会朝着全局最小值方向移动。
如果你不熟悉导数或者微积分,也不熟悉dJ(w)/dw的含义,不要着急,在下一个视频中,我们会讨论更多关于导数的知识。如果你很了解微积分,你应该对神经网络是如何工作的,有更深刻更直观的认识。但即使你并不熟悉微积分,通过下面的几个视频,我们也会对导数和微积分,有足够的直观认识。你将能够有效地使用神经网络,但现在所有的直观认识,即这个术语,表示的是函数的斜率。
我们知道,用目前参数的情况下,函数的斜率朝下降速度最快的方向走。我们知道,为了让成本函数J走下坡路,下一步更新的方向在哪。当前J(w)的梯度下降法,只有参数w。在 logistic 回归中,你的成本函数,是一个含有w和b的函数。在这种情况下,梯度下降的内循环,就是这里的这个东西。你必须一直重复计算,通过w:=w - α * dJ(w,b)/dw更新w,通过b:=b - α * dJ(w,b)/db更新b。这两个等式是,实际更新参数时进行的操作。
另外我想提到的是,在微积分的符号约定中,对一些人来说是有点困惑的。目前我并不认为,理解微积分是非常重要的。如果你看到了这些,希望你不要想太多。在微积分中在这里的术语,是这个有趣的花体符号,这个符号其实是 一个小写d,用一个花哨字体来写的。当你看到这种表示方式时,意思是J(w,b)的导数,或者函数J(w,b)的斜率,就是函数在w方向的斜率是多少。
在微积分中这个符号的规则,我认为并不是完全符合逻辑的。我认为这样会导致更加复杂。当函数J有两个以上的变量,不使用小写字母d而使用花哨的符号,这个就被称为偏导数符号。但别担心,如果J只有一个变量,就是用小写字母d。唯一的区别就是,你是用偏导数符号,还是小写字母d,是取决于你的函数J是否含有两个以上的变量。变量超过两个就用偏导数符号,如果函数只有一个变量就用小写字母d。
这是在微积分里一个有趣的符号规则,我认为它使事情变得更加复杂了。但如果你看到了偏导数符号,其含义就是,计算函数关于其中一个变量,在对应点所对应的斜率。类似在这里,形式上应该用微积分中的正确符号,因为在这里J有两个输入,而不是一个。屏幕底部的这个,应该用这个偏导数来写,但是其实表达的和小写字母d一样。
最后当你编写代码,想要实现屏幕写出的这个式子时,通常在更新w的值时我们会用dw这个变量,来代替这个式子。对于这个量呢,当你想去更新b的数值,代码中就用db来表示。
综上这就是梯度下降法的实现方法,如果你有几年没碰过微积分了,我知道微积分中有很多的导数,你可能会更适应。如果你有这种感觉,也不要担心,在下一个视频中,我会更直观地来给你讲解导数。不需要很深入理解微积分,而只是直观地理解微积分,你也可以让神经网络变得更有效。
让我们进入下一个视频课程,一起来多讨论一下导数。