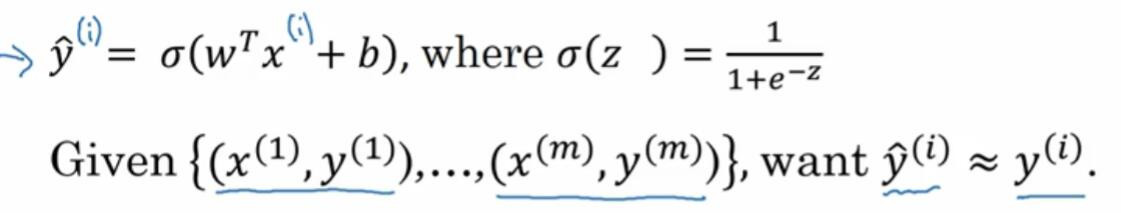在上一个视频中,你看到的是 logistic 回归的模型。为了训练 logistic 回归模型的参数w以及b,需要定义一个成本函数。让我们来看一下,用于训练 logistic 回归的成本函数。
回忆一下,这是上一张幻灯片的函数,所以你的输出y_hat=sigmoid(w^Tx+b),这里定义为sigmoid(z)。为了让模型通过学习来调整参数,要给一个m个样本的训练集,很自然地,你想通过在训练集找到参数w和b,来得到你的输出。
对训练集的预测值,写成y_hat^(i),我们希望它会接近于训练集中的y^(i)值。为了让上面的方程更详细一些,需要说明上面这里定义的y_hat,是对一个训练样本x来说的。对于每个训练样本,我们使用这些带有圆括号的上标,方便引用说明还有区分样本。你的训练样本(i)对应的预测值是y_hat^(i),是用训练样本,通过
sigmoid 函数作用到wT*x^(i)+b得到的。
你也可以将z^(i)定义成这样,z^(i)等于wT*x^(i)+b。在这门课里,我们将使用这个符号约定,就是这个上标(i)来指明数据,表示x或者y或者z和第i个训练样本有关。这就是上标(i)的含义。
现在我们来看看损失函数,或叫做误差函数,它们可以用来衡量算法的运行情况。你可以定义损失为,y_hat和y的差的平方,或者它们差的平方的1/2。结果表明你可以这,样做但通常在 logistic 回归中,大家都不这么做。因为当你学习这些参数的时候,你会发现之后讨论的优化问题,会变成非凸的。最后会得到,很多个局部最优解。梯度下降法可能找不到全局最优值。如果你不理解这几句话,别担心,我们会在后面的视频中讲到它。
但是这个的直观理解就是,我们通过定义这个损失函数L,来衡量你的预测输出值y_hat和y的实际值有多接近。平方误差看起来似乎是一个合理的选择,但用这个的话,梯度下降法就不太好用。
在 logistic 回归中,我们会定义,一个不同的损失函数,它与平方误差有相似的作用。这些会给我们一个凸的优化问题,在后面的视频能看到,它很容易去做优化。在 logistic 回归中,我们会使用这里写的损失函数。它是-(y*log(y_hat) + (1-y)log(1-y_hat))。
直观地看看为何这个损失函数能起作用。记得如果我们使用平方误差,它越小越好。对于这个 logistic 回归的损失函数,同样地,我们也想让它尽可能地小。为了更好地理解,为什么它能够起作用,让我们来看两个例子。
在第一个例子中,我们说y=1时,损失函数就正好是第一项,L(y_hat,y),带个负号,就是-log(y_hat)。因为如果y=1那么第二项1-y就等于0。这就是说当y=1时,你想让-log(y_hat)尽可能小,这就是说想让log(y_hat)足够大,这就是说,你想要y_hat足够大。但是因为y_hat是
simoid 函数得出的,永远不会比1大。也就是说,如果y=1时,你想让y_hat尽可能地大,但它永远不会大于1,所以你要让y_hat接近1。
另一个情况就是如果y=0,损失函数的第一项等于0,然后第二项就是这个损失函数。损失函数变成-log(1-y_hat)。在学习过程中,想让损失函数小一些,也就是说,你想要log(1-y_hat)够大,因为这里有一个负号。通过这一系列推理,你可以得出,损失函数让y_hat尽可能地小。同样,因为y_hat只能介于0到1之间,这就是说,当y=0时,损失函数会让y_hat尽可能地接近0。
有很多函数都能达到这个效果,如果y=1我们尽可能让y_hat很大 ,如果y=0尽可能让y_hat足够小。绿色字体这里稍微解释了,为什么用这个作为损失函数。后面我们会提供选修视频,给出这样做的更正式的原因。解释为什么在 logistic 回归中,要用这个形式的损失函数。
最后说一下,损失函数是在单个训练样本中定义的。它衡量了,在单个训练样本上的表现。下面我要定义一个成本函数,它衡量的是在全体训练样本上的表现。这个成本函数J,根据之前得到的两个参数w和b,J(w, b)等于,1/m * ∑L(y_hat^(i), y^(i)),即所有训练样本的损失函数和。而y_hat是用一组特定的参数w和b,通过
logistic 回归算法得出的预测输出值。所以把这个展开,这等于-1/m乘以从i=1到m的损失函数的和。我在这里画上方括号,负号在这一堆式子的外面。
术语这样来用,损失函数只适用于像这样的单个训练样本。这个成本函数是基于参数的总成本。所以在训练 logistic 回归模型时,我们要找到合适的参数w和b,让下面这里的成本函数J尽可能地小。
你刚刚看到了 logistic 回归算法的过程,以及训练样本的损失函数,还有和参数相关的总体成本函数。结果表明 logistic 回归可以被看作是 一个非常小的神经网络。
在下一个视频里 我们将会学到,直观地去理解神经网络能做什么。继续看下一段视频,看看如何将 logistic 回归,看作一个非常小的神经网络。