文章来源:sas 翻译:孙菁
文章投稿:news@top25.cn
导读:对于数据科学或数据分析,机器学习已成为解决问题的一大利器。本文意在面向刚刚入门数据分析的初学者,或对利用机器学习处理数据感兴趣的读者,提出一些实用的建议与指导。
作为一个数据分析的初学者,当面对各式各样的机器学习算法时通常会问:我究竟该用哪种算法呢?
答案取决于诸多因素,包括:
· 数据量的大小、数据的质量和特质。
· 可用的计算时间。
· 任务的紧急性。
· 对数据进行何种处理。
很多时候,在没有尝试各种算法之前,即使一个经验丰富的数据科学家也不能肯定地说出哪种算法能取得最好的结果。但在一些因素的限制下,我们通常会选择某一种算法作为我们的第一次尝试。本文就是希望为初学者在苦恼地纠结于该选择何种算法,迈出第一步时提供一些实用的建议和指导。
机器学习算法技巧图
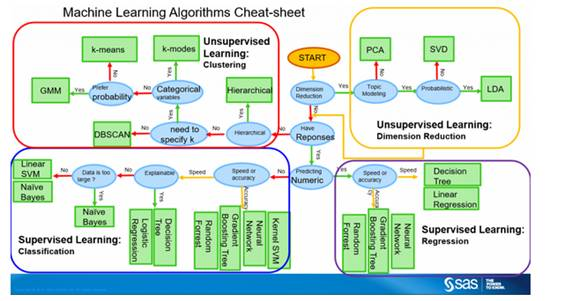
这张机器学习算法技巧图可以帮助你从五花八门的机器学习算法中找出最适合你的实际问题的算法。接下来的部分会详细的将为你讲解如何来使用这张图。
由于这张图是为初学者设计,因此图中的算法做了一些较为简单的假设。
通过一些数据科学、机器学习方面的专家和开发者的反馈及建议,我们归纳并整理出了这张技巧图。有些问题存在不同的观点,对这些问题的解读,在本文中我们会试图突出其共性并调和其差异。
除图中已有的算法之外,未来我们会逐步添加更多的可用的算法。
如何使用技巧图
按“if<路径标签>then use<算法>”这种方式,仔细观察图中箭头所示的路径及标签。例如:
· 如果想解决降维(DimensionDeducing)的问题,那么你可以采用主成分分析算法(PCA)。
· 如果要进行快速数值预测(PredictingNumeric, Speed),那么可以选择决策树(Decision Tree)或逻辑回归算法(LinearRegression)。
· 如果想得到分层次的结果(Hierarchical),那么可以使用分层聚类算法(Hierarchical)。
但是,有的问题在图中可能会有多于一条分支的算法,相反,也有的问题可能找不到合适的算法。所以读者们应将本图中的算法当做经验法则的建议,其中有些建议可能并不准确。事实上,很多数据科学家都表示,找到最优算法的唯一方法就是尝试所有的算法。
机器学习算法的种类
本节会概述目前最受欢迎的几类机器学习算法。如果你对这几类算法已经相当熟悉,你可以跳过这一部分并直接转到“特定算法选择”这一节。
有监督学习算法
有监督学习算法是基于样本集做出预测。比如,某商品的历史的销售记录可以用来预测其未来的价格。有监督学习算法的输入数据(即训练集)包括用于处理的数据和期望的输出变量(即标签)。处理过程中,算法会分析训练数据并学习到一个用于从输入映射到输出的函数。之后,这个函数具有的泛化能力就能够将新的、训练集中不存在的数据(无标签)映射到所期望的输出。
· 分类问题:当输入数据用于预测其所属类别,即预测值是离散值时,有监督学习被称为分类问题。例如我们想通过算法识别一张图片是狗还是猫。当标签数即类别数为二时,叫做二分类问题,当标签数大于二时为多分类问题。
· 回归问题:当预测值是连续值时被称为回归问题。
· 预测问题:基于过去和当前的数据对未来数据进行预测的问题,常用于分析某事件的趋势。一个常见的例子就是基于某商品前几年和当年的销售情况,对未来几年的销售做出预测。
半监督学习
有监督学习面临的挑战之一是训练数据提前标签化的开销可能会比较大。在标签数量有限的情况下,我们可以通过没有标签的样本来增强有监督学习。由于这种情况下算法并不是完全的有监督学习,因此我们称之为半监督。利用半监督学习算法,我们可以使用不带标签的样本和少量带标签的样本来提高学习算法的准确率。
无监督学习
用于训练的数据完全无标签时,即是无监督学习算法。此时算法需要自动地发现数据中潜在的固有关系模式,如聚类结构,低维流形,稀疏树或图。
· 聚类问题:将样本数据集进行分组,使得某样本与同组中的数据与不同组的数据相比,与前者更为相似(按照某些标准)。这种模型通常被用于将整个数据集划分为几个组,用户可通过对每一组的分析来找到数据中固有的关系模式。
· 降维:在一定条件内减少变量的数量。在很多问题中,原始数据会是高维的特征表示,但其中可能有冗余或不相关的特征。因此,对原始数据进行降维可以帮助我们找到数据之间真正的潜在关系。
强化学习
强化学习是基于环境的反馈信息,对代理(agent)行为做出分析和优化的算法。此时机器不是被指示该采取哪个行为,而是会自主地尝试不同的行为并找到能够获得最优反馈的行为。测试和错误、延迟反馈是使强化学习算法区别于其他机器学习算法的特征。
选择算法时的考虑
当你准备选择一个算法进行实验时,要时刻考虑到训练所用时间及算法的易用性。很多用户在选择时会优先考虑准确性,而初学者更多地倾向于选择他们最熟悉的算法。
当你得到一个数据集时,你首先要考虑的应该是如何获得结果,而不要在意这些结果是好是坏。虽然初学者更倾向于选择易于实现且能快速得到结果的算法,但只要这只是数据处理过程中的第一步,你可以这样选择。当得到了一些分析结果并对数据更为熟悉时,你可以再花费更多的时间使用更复杂的算法来加强你对数据的理解,从而进一步改善结果。
分析到了此阶段,实际最好的算法也许并不是目前得到了最高准确率的算法,因为一个算法通常需要仔细的调整和广泛的训练才能得到更好的可实现结果。
特定算法选择
对每个算法进行更深入的理解可以帮助你更清楚地知道它们提供了什么样的功能以及如何使用它们。这一节提供这些算法更具体的内容,并给出何时使用何种算法的一些建议,与上文中的技巧图相一致。
线性回归和逻辑回归
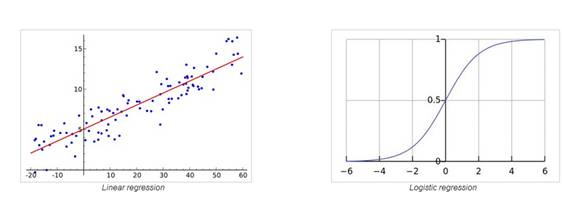
线性回归是用来对取值连续的因变量y和一个或多个预测因子X之间关系的模型。y和X之间的关系可以用线性关系y=β^TX+ϵ 来近似。给定训练集样本{x_i,y_i}N_i=1,算法可以学习线性关系中的参数集β。
当y的取值为离散值时,则可以通过logit链接函数将线性回归函数变换为逻辑回归函数。逻辑回归算法是一个简单、快速且强大的分类算法。这里我们讨论二分类的情况,即因变量y只能取两个值{y_i∈(−1,1)}N_i=1 (可以很容易地扩展到多分类的问题)。
在逻辑回归问题中,我们使用不同的假设类来预测一个给定样本分别属于类“1”和类“-1”的概率。具体来说,算法会学习得到p(y_i=1|x_i)=σ(β^Tx_i) 和 p(y_i=−1|x_i)=1−σ(β^Tx_i)的函数。这里σ(x)=1/(1+exp(−x))是sigmoid函数。给定训练样本集{x_i,y_i}N_i=1,通过最大化 β的似然函数就可以学习参数集 β。
线性SVM和内核SVM
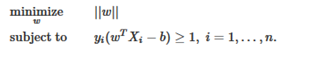
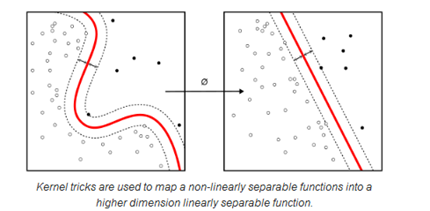
内核的技巧通常用于将非线性可分离函数映射到更高维的线性可分离函数。支持向量机(SVM)算法以一个用向量w和偏置值b表示的超平面(即边界)作为分类器。超平面可以通过使不同类的样本点之间的距离最大来区分不同的类别。因此,问题可被描述为一个约束最优问题:
当类别不能被线性分离时,内核技巧就可以将非线性的可分离空间映射到高维的线性可分离空间。
当分类问题中的大多数因变量是数字数值时,可以首先考虑使用逻辑回归和SVM算法。这两个算法易于实现,算法中的参数也较容易调整,而且性能也非常好。因此这两个算法很适合初学者实践。
决策树预测模型
决策树、随机森林及梯度增强算法都是基于决策树的算法。很多在决策树算法基础上改进的算法做的都是同一件事—将特征空间分割为多个拥有大部分相同的标签的子空间。决策树的原理易于理解和实现。但是,如果处理过程中用尽决策树的树枝并且到达决策树深层时,该算法容易出现过度拟合的问题。随机森林和梯度增强算法既能够达到很好的准确率又能克服以上问题,因此被广泛使用。
神经网络和深度学习
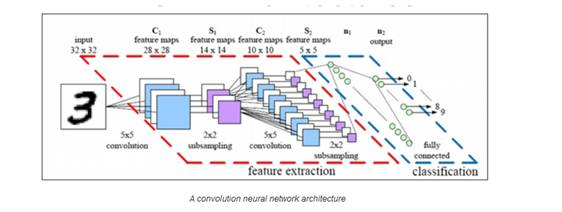
20世纪80年代中期,由于并行和分布式处理计算的发展,神经网络蓬勃发展,但又由于神经网络优化参数的反向传播算法的无效性而受到阻碍。用于解决凸函数最优化问题的SVM等其他更简单的算法,开始逐渐取代机器学习中神经网络算法。
近年来,改进的训练技术如半监督预训练和分层贪婪训练技术,以及逐渐增强的硬件计算能力如GPU和MPP等,使得神经网络再次兴起,甚至出现了几千层的神经网络。
换句话说,当初的浅层神经网络已经进化为深度学习的深层神经网络。深层神经网络已经非常成功地应用在有监督机器学习方面。在语音和图像识别领域,深度学习展现了非常好的性能,有时甚至能超越人类。在半监督学习任务例如特征提取中,深度学习也能够在少量的人工干预下完成从原始语音或图像中对特征的有效提取。
神经网络的结构包括三部分:输入层、隐藏层和输出层。训练样本同时决定了输入层和输出层。当输出层输出离散值时,网络可用于解决分类问题;当输出层输出连续值时,网络可用于解决回归问题;当输出层与输入层相同时,网络可以提取数据的内在特征。隐藏层中节点的个数决定了网络的复杂度和网络解决问题的能力。
k-means/k-modes, GMM (Gaussian mixture model)聚类

k-means/k-modes, GMM (Gaussian mixturemodel)等聚类算法的目的在于将n个观察点划分为k个聚类。K-means算法进行硬分配,即每个样本有且只有一个与之相关联的聚类。而GMM算法则对每个样本进行软分配,即每个样本与每个聚类都以一定的概率相关联。这两个算法都相对简单,当聚类数k给定时,训练速度也相对较快。
DBSCAN
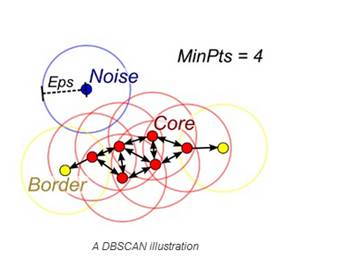
当聚类数k未知时,DBSCAN(density-basedspatial clustering)算法可用于通过密度扩散来连接样本。
Hierarchical clustering
分层聚类
分层聚类可被看做利用的树的结构。该算法不需要输入聚类数k,并且可以使用不同的k来进行不同的粒度级(即可以细化/粗化聚类)的划分。
PCA, SVD 和LDA
由于原始输入特征中可能包含不相关的特征,或者“本质的”特征维数可能小于输入的特征维数,所以我们并不希望将巨大的原始特征直接输入到机器学习算法。这时,我们就需要PCA, SVD 和LDA等算法对高维特征进行降维。
PCA是一种无监督聚类算法,用于将高维数据空间映射到低维空间,同时尽可能多地保留原始信息。具体来说,PCA会找到一个能最大保留数据方差信息的子空间,该子空间由数据协方差矩阵的主要特征向量定义。
SVD与PCA相关,这是因为,与PCA定义了子空间类似,中心数据矩阵(特征与样本)的SVD也由主左奇异矢量定义了子空间。然而,SVD是一种更通用的技术,因为它可能做到PCA做不到的事情。例如,用户vs电影数据矩阵的SVD能够提取可用于推荐系统使用的用户主资料和电影资料。此外,SVD也在自然语言处理(NLP)中被广泛用作主题建模工具,被称为潜在语义分析模型。
在NLP中,一个相关的技术是LDA(Latent Dirichletallocation)。这是一个概率主题模型,与GMM可以将连续型数值分解到高斯密度类似,它可以将文本分解到主题。与GMM不同的是,LDA是对离散型数据进行建模(单词和文本),并且模型中的主题是被限制为服从Dirichlet分布的先验分布。
结论
让我们来总结一下解决问题的主要步骤:
· 定义问题,你想解决的问题是什么?
· 从简单算法开始,熟悉数据及基本结果。
· 尝试更复杂的方法。
SAS Viya Data Mining and MachineLearning(https://support.sas.com/documentation/prod-p/vdmml/index.html) 为初学者提供了一个机器学习及应用的很好的平台,感兴趣的读者可以进行更深入的学习。