不得不承认这篇文章在理论方面的贡献还是比较有限的，而且也确实受到了大家的质疑，但是它的意义还是很重大的，相信评委选定它为oral paper也是看中了它对未来研究的影响力。这里不妨带领大家看看它里面的一些论断。
论文里一个看上去并不新鲜的论断就是：深层模型是可以“背下所有训练数据的”，为了证明这一点，作者先用一个深到没朋友的复杂模型去解决一个相对简单的cifar10数据集（说实话现在很多模型都可以做到100%的训练集精度），接下来作者就开始调皮了，它破坏数据的label，将训练数据里面的label作随机变换；然后又改图，将训练数据里面的图像做了改变。经过这两种改变，图像信息和类别信息在语义上已经无法匹配了，如果让一个正常人来看的话，这些图像是无法得到所对应的类别的。那么对于深层模型来说，这样的任务可以学习么？
最后的结论是，当然可以。即使问题变得毫无逻辑毫无人性，在冷酷的深层模型面前，这个问题一样可以解决。于是作者觉得——它会不会把题目都背下来了？
其实站在人类的角度去理解，模型确实有可能背下来了。但是如果抛开人类几千年的文明来看，也许存在某一种奇异的生物，它恰好可以解码某种特殊的图像——标签对呢？那些随机图片在它们的文明世界就是又某种具体的代表呢？这种感觉和我们看一种不认识的语言类似。如果我们认同这些图像——标签对背后可能存在的逻辑和文化，那么模型的表现就没那么奇怪了。
当然，从实验本身来看，过拟合的现象是一定存在的。后面为了证明神经网络又过拟合的能力，作者给出了一个实现网络过拟合的可行性方案。下面就来详细介绍这个方案。
过拟合方案
我们假设有一个简单的数据集：
x^T=[
[0.2, 0.3, 0.6],
[0.5, 0.7, 0.1],
[0.3, 0.4, 1],
[0.3, 0.3, 0.3]
]
它的label如下所示：
y=[1 1 0 1]
我们能不能构建一个网络，使得这个数据集完美拟合呢？答案是可以的。对于一个维度为d的n个数据组成的数据集，我们可以用2n+d个数据将数据集完美拟合。对于这个问题，我们只需要一个有11个参数的2层神经网络。其中第一层的输出为n，也就是4。
首先，我们选择一个第一层的参数：
w1=[
[1 1 1]
[1 1 1]
[1 1 1]
[1 1 1]
]
这个参数有一个特点，那就是每一行的参数都一样，下面的参数实际上是复制了上面的参数。
这样经过点乘，可以得到：
w1*x=[
[1.1 1.3 1.7 0.9]
[1.1 1.3 1.7 0.9]
[1.1 1.3 1.7 0.9]
[1.1 1.3 1.7 0.9]
]
其实在前面我们也曾介绍过，这种参数完全一致的模型实际上是一种退化了的模型。
下面的过程就有技巧了，我们设计了一些特殊的偏置项：
b1^T=[-0.8, -1.0, -1.2, -1.6]
计算后得到：
w1*x+b1=[
[0.3, 0.5, 0.9, 0.1]
[0.1, 0.3, 0.7, -0.1]
[-0.1, 0.1, 0.5, -0.3]
[-0.5, -0.3, 0.1, -0.7]
]
然后让这个网络经过ReLU，得到：
ReLU(w1*x+b1)=[
[0.3, 0.5, 0.9, 0.1]
[0.1, 0.3, 0.7, 0]
[0, 0.1, 0.5, 0]
[0, 0, 0.1, 0]
]
下面呢？我们用这个中间结果乘以某一个参数w2，让它得到最终结果y。我们采用反解的方式把w2求解出来：
w2^T = [
0.9, 0.4, 0.1, 0
]
这样问题就得到了解决。通过这种方式我们把完美解决这个数据集的方法展现出来。
过拟合方案的证明
那么这个方案可不可以用形式化的方式证明呢？可以的。实际上这个方法使用了2层神经网络，下面就列出这个神经网络的计算方法：
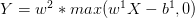
这里x是d维的，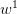
是n*d维的，但是由于每一行的数据是相同的，所以它相当于只有d维参数。
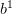是n维的，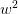
是n维的。这就是我们所使用到的所有参数：2n+d。
下面的第一步，我们希望找到一组参数w1，使得不同的数据与它相乘的结果是不同的。这里用z来表示，也就是说对于n个数据，存在某种排序pn，使得：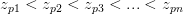
。我们不妨假设p1=1,p2=2，于是，这个n*n的矩阵就变成了：
[
[z1, z2, ... ,zn]
[z1, z2, ... ,zn]
......
[z1, z2, ... ,zn]
[z1, z2, ... ,zn]
]
第二步，由于这个序列是一个有限序列，那么就可以找到另一序列{bn}用于表示偏置项，这个序列有下面的特点：
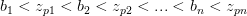
这样经过计算，再经过relu层，就得到了：
[
[z1-b1, z2-b1, ... , zn-b1]
[0, z2-b2, ..., zn-b2]
[0, 0, z3-b3, ..., zn-b3]
...
[0, 0, 0, ..., 0, zn-bn]
]
可以看出这是一个上三角矩阵（这里和原论文的证明稍有不同，论文中得到的是下三角矩阵），只要对角线不为0，那么这个矩阵就是一个满秩的矩阵，对于形如：
Ax=b
这样的解方程问题，方程存在唯一解，因此，无论最终的结果如何，从上面的矩阵出发乘以一个参数就可以得到任意的结果。
sgd与过拟合
论文中还提到关于sgd对过拟合的防止作用，其实从深层模型的角度，还可以有别的理解方法。在前面我们曾经聊过参数的稳定性问题。为了保证参数稳定，参数的初始化以及更新过程都会保证每一层参数的均值方差控制在一定的范围内，这就相当于对参数进行限制。如果深层模型的参数像浅层模型那样可以野蛮生长，那么带来的结果并不仅仅是过拟合，更有可能的是直接溢出。
所以从这个角度来看，为了保证模型是可用的，优化过程已经隐含了l2正则这样的正则项。所以我们再加入l2正则项虽然可以起到效果，但确实不是唯一起作用的。
对于深层模型泛化的猜想
既然论文中提到了深层模型的过拟合能力，和本身所具备的泛化能力，那么这个泛化能力究竟是从何而来呢？这里提一点自己的猜想。我觉得通过过拟合来实现模型泛化也是有希望的，但是需要基于一个前提：
模型的输入空间——也就是图像空间在某个临域内具备泛化能力。
可以想象一下传统的机器学习模型，它们的模型相对清晰好分析，于是前辈们可以用一些量化指标来分析模型的复杂程度，像vc维那样的指标。但是到了深层模型这里，模型表示和优化都发生了变化，很多曾经的指标变得不那么好用了。在机器学习的课本上曾经讲过，2阶模型的泛化性比10阶模型的泛化性强，但是对于深层模型来说，参数数量、模型结构对模型的复杂度都会产生影响，大家用的都是10阶复杂度的模型，所以从模型结构判断复杂度已经不太容易了。
那么深层模型的泛化从何而来？由于深层模型毕竟还是一个可导的模型，我们就不由地猜想，这个模型是否能够满足Lipchitz那样的条件呢？也就是说对于某一个训练数据，如果模型已经将它的映射学习好，那么
1. 对训练数据稍作改动，但不改变数据的本质，这个映射是否还能保持正确呢？
2. 对训练数据作关键性改动，这个映射的结果是否会改变呢？
之前我们聊过类似的话题，结果大概可以佐证，我们训练的模型是可以满足这个条件的，只不过这个临域不会很大。而且这个临域绝不是我们平时想象的开球集合
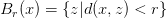
它应该是一个比较奇怪的形状。
如果这个条件说得通，那么深层模型的泛化问题就可以用这样的方式描述了：
1. 我们知道两个集合X和Y，存在某个映射使得每一个x都对应一个y；
2. 有训练数据对{x,y}，其中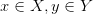
，经过深层模型计算，这些点的映射都可以被完美完美学习出来；
3. 根据上面的假设，x附近的临域由于模型的局部泛化能力而得以满足；
4. 如果训练数据足够多，临域的范围足够大，以至于它们组合起来可以将整个输入集合“盖住”或者“基本盖住”，那么我们就可以认为模型通过过拟合的手段获得了泛化能力。因为我们很难证明输入的空间是一个紧空间，所以我们的目标只能是用有限个开覆盖“基本盖住”，完全“盖住”有些困难。
从上面的猜测来看，留给模型施展拳脚的地方共有两个：
1. 补充足够多的数据——这是每一个作深度学习的童鞋都在做的事情
2. 让局部泛化的范围变大——这个就有些抽象了。l2正则限制参数的大小，可以让模型在局部表现的比较平滑，从而起到一些效果；batch normalization也限制了模型，所以某些时候它可以起到一些效果。
所以我猜想未来会有大神从第2点发力，发明更多的让模型更容易局部泛化的结构，这样模型整体的泛化能力也就更容易提高。
以上内容纯属猜测，期待有更多的理论被证实，也欢迎来打脸。
