距离春节放假倒计时第二天,办公室大家明显没心思干活啦,从早聊到晚。对于我这样的脑袋要秃掉的人来说,真的是雪上加霜,为了不受影响,真的是一天都在碎碎念知识点。
今天算了一下假期的安排,发现可以做的事情还是很多的,争取每天来打卡。

以下是今天的笔记,发现随着时间的推移,好像又可以沉浸在思考里了,没有一开始学习那么痛苦了,加油。
1.梯度下降的直观理解
关于学习效率的设置:



由以上可知,当我们接近局部最低点时,即从品红色往绿色方向迭代时,梯度下降法会自动采取更小的幅度,这是因为当我们接近局部最低点时,很显然再局部最低时导数等于零,所以当我们越接近局部最低时,导数值会自动变得越来越小,所以梯度下降讲自动采取较小的幅度,这就是梯度下降的做法。所以实际上没有必要再另外减小a.
2.梯度下降的线性回归


batch :gradient descent
这就是我们所说的批量梯度下降法,意味着对所有样本进行批量下降处理,也有不需要对所有样本,而是其中部分子集进行处理的算法。
3.多变量梯度下降
- 针对多变量线性回归,代价函数:J(θ0,θ1…θn)=2m1∑i=1m(hθ(x(i))−y(i))2,其中:
hθ(x)=θTX=θ0+θ1x1+θ2x2+⋯+θnxn,我们的目标同样是找出使得代价函数最小的一系列参数。其批量梯度下降算法为:
Repeat {
θi:=θj−α∂θj∂J(θ0,θ1,…,θn)
}
即:
Repeat {
θj:=θj−α∂θj∂2m1∑i=1m(hθ(x(i))−y(i))2
}
求导数后得到:

我们开始随机选择一系列的参数值,计算所有的预测结果后,再给所有的参数一个新的值,如此循环直到收敛。
代码示例:
计算代价函数J(θ)=2m1∑i=1m(hθ(x(i))−yi)2 其中:hθ(x)=θTX=θ0x0+θ1x1+θ2x2+⋯+θnxn
Python 代码:
def computerCost(X,y,theta):
inner = np.power(((x*theta.T)-y),2)
return np.sum(inner)/(2*len(x))
4.梯度下降法实践
4.1特征缩放
在面对多维特征问题的时候,要保证这些特征都具有相近的尺度,这可以帮助梯度下降算法更快地收敛。

4.2学习率
-
梯度下降算法的每次迭代受到学习率的影响,如果学习率α过小,则达到收敛所需的迭代次数会非常高;如果学习率α过大,每次迭代可能不会减小代价函数,可能会越过局部最小值导致无法收敛。
-
通常可以考虑尝试以下学习率:
α=0.01,0.03,0.1,0.3,1,3,10
4.3特征和多项式回归
- 有时,线性回归并不适用于所有数据,我们需要曲线来适应我们的训练集,比如一个二次方模型:hθ(x)=θ0+θ1x1+θ2x22
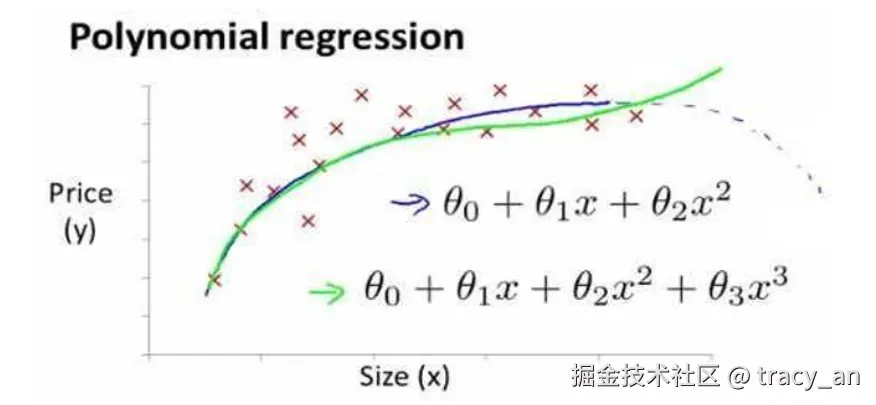
- 通常我们需要先观察数据再决定尝试怎样的模型,我们可以让x2=x22,x3=x33,从而将模型转化为线性回归模型。
 ==如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。==
如下图,未缩放之前,曲线模拟会得到随着size的增加,超过一定范围后,price开始下降。
==如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。==
如下图,未缩放之前,曲线模拟会得到随着size的增加,超过一定范围后,price开始下降。

==如果我们采用多项式回归模型,在运行梯度下降算法前,特征缩放非常有必要。==
如下图,未缩放之前,曲线模拟会得到随着size的增加,超过一定范围后,price开始下降。