YOLO26改进 - SPPF模块 发论文神器！LSKA注意力改进SPPF,增强多尺度特征提取能力，高效涨点！！！

pick1
2 阅读7分钟

前言

本文介绍了Large Separable Kernel Attention (LSKA)模块及其在YOLO26中的结合应用。LSKA旨在解决Visual Attention Networks (VAN)使用大内核卷积时的计算效率问题，通过将2D深度卷积层的卷积核分解为级联的水平和垂直1-D卷积核，降低了计算复杂度和内存占用，且使VAN更关注物体形状。我们将集成LSKA的SPPF_LSKA模块引入YOLO26，大量实验表明，改进后的模型在对象识别、检测、分割和稳健性测试上表现出色。

文章目录： YOLO26改进大全：卷积层、轻量化、注意力机制、损失函数、Backbone、SPPF、Neck、检测头全方位优化汇总

专栏链接: YOLO26改进专栏

@[TOC]

介绍

image-20240527212823405

摘要

配备大卷积核注意力（LKA）模块的视觉注意力网络（VAN）在多种视觉任务中展现出卓越性能，超越了视觉Transformer（ViTs）的表现。然而，LKA模块中的深度卷积层随着卷积核尺寸的增大，会导致计算复杂度与内存占用的二次增长。为解决此问题并实现在VAN注意力模块中使用超大卷积核的目标，本研究提出了一个名为LSKA的大可分卷积核注意力模块家族。LSKA通过将深度卷积层的二维卷积核分解为串联的水平与垂直一维卷积核，实现了对标准LKA设计的改进。这种分解策略使得无需额外模块即可在注意力模块中直接使用配备大卷积核的深度卷积层。实验验证表明，在VAN中部署的LSKA模块能够在显著降低计算复杂度与内存占用的同时，达到与标准LKA模块相当的性能水平。研究还发现，随着卷积核尺寸的增加，所提出的LSKA设计使VAN更加关注物体形状特征而非纹理信息。此外，我们在五种受损版本的ImageNet数据集上对VAN、ViTs以及最新ConvNeXt架构中的LKA和LSKA模块进行了系统性稳健性基准测试，这些数据集在先前研究中较少被探索。大量实验结果表明，随着卷积核尺寸的增大，所提出的VAN中LSKA模块显著降低了计算复杂度与内存占用，同时在目标识别、目标检测、语义分割及稳健性测试中表现优于ViTs和ConvNeXt，并与VAN中LKA模块保持相当性能。相关代码已公开于github.com/StevenLauHK…

文章链接

论文地址：论文地址

代码地址：代码地址

基本原理

Large Separable Kernel Attention (LSKA)是一种新颖的注意力模块设计，旨在解决Visual Attention Networks (VAN)中使用大内核卷积时所面临的计算效率问题。LSKA通过将2D深度卷积层的卷积核分解为级联的水平和垂直1-D卷积核，从而实现了对大内核的直接使用，无需额外的模块。

概述

  1. 基本设计：

    • LSKA将2D深度卷积层的卷积核分解为级联的水平和垂直1-D卷积核。
    • 这种分解设计使得LSKA可以直接使用深度卷积层的大内核，无需额外的模块或计算。

  2. 计算效率：

    • LSKA的设计降低了参数数量的增长，从而降低了计算复杂度和内存占用。
    • 通过级联1-D卷积核的方式，LSKA在处理大内核时能够保持高效性能。

  3. 形状和纹理偏好：

    • LSKA设计使得模块更加偏向于对象的形状而非纹理。
    • 这种偏好有助于提高模型对对象形状的学习能力，从而提高模型的鲁棒性和泛化能力。

总的来说，LSKA通过巧妙的卷积核分解设计，实现了对大内核的高效利用，同时保持了模型的性能和鲁棒性。其技术原理使得LSKA成为一种有潜力的注意力模块设计，可以在VAN等视觉任务中发挥重要作用。

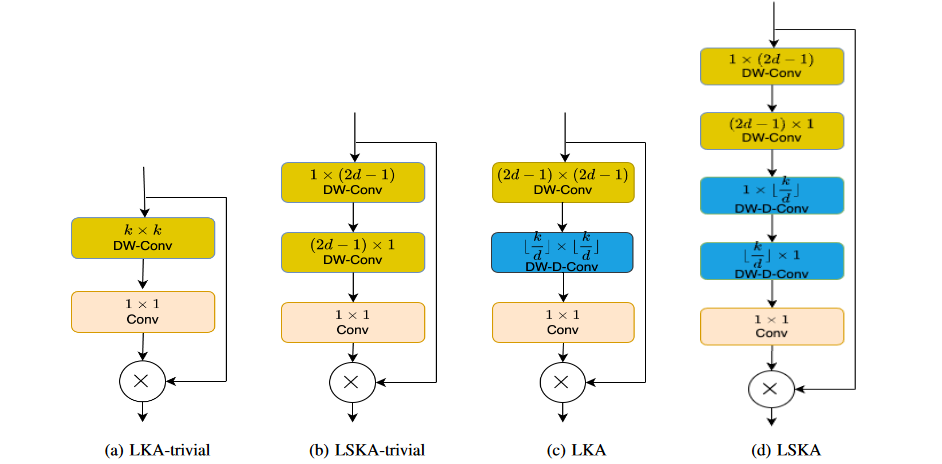
与LKA-trivial、LSKA-trivial和LKA的比较：

image-20240527213758579

  • LKA-trivial是一种简单的注意力模块设计，使用深度卷积和大内核，但会导致参数数量的二次增长。

  • LSKA-trivial是对LKA-trivial的改进，通过可分离卷积核的级联降低了参数数量的增长，提高了计算效率。

  • LKA是原始的Large Kernel Attention设计，包括标准深度卷积、扩张深度卷积和1x1卷积，但在处理大内核时会带来计算和内存开销。

  • LSKA通过级联1D卷积核的设计，有效地解决了LKA中大内核带来的问题，在保持性能的同时降低了计算复杂度和内存占用。

核心代码

import torch
import torch.nn as nn

# 定义一个名为LSKA的神经网络模块类，继承自nn.Module
class LSKA(nn.Module):
    def __init__(self, dim, k_size):
        # 初始化LSKA类，dim为通道数，k_size为卷积核大小
        super().__init__()

        self.k_size = k_size  # 保存卷积核大小

        # 根据k_size的不同值，初始化不同的卷积层
        if k_size == 7:
            # 水平和垂直方向上的第一层卷积
            self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,(3-1)//2), groups=dim)
            self.conv0v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=((3-1)//2,0), groups=dim)
            # 空间卷积层，带有膨胀参数
            self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,2), groups=dim, dilation=2)
            self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=(2,0), groups=dim, dilation=2)
        elif k_size == 11:
            self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 3), stride=(1,1), padding=(0,(3-1)//2), groups=dim)
            self.conv0v = nn.Conv2d(dim, dim, kernel_size=(3, 1), stride=(1,1), padding=((3-1)//2,0), groups=dim)
            self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,4), groups=dim, dilation=2)
            self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=(4,0), groups=dim, dilation=2)
        elif k_size == 23:
            self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)
            self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)
            self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 7), stride=(1,1), padding=(0,9), groups=dim, dilation=3)
            self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(7, 1), stride=(1,1), padding=(9,0), groups=dim, dilation=3)
        elif k_size == 35:
            self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)
            self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)
            self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 11), stride=(1,1), padding=(0,15), groups=dim, dilation=3)
            self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(11, 1), stride=(1,1), padding=(15,0), groups=dim, dilation=3)
        elif k_size == 41:
            self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)
            self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)
            self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 13), stride=(1,1), padding=(0,18), groups=dim, dilation=3)
            self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(13, 1), stride=(1,1), padding=(18,0), groups=dim, dilation=3)
        elif k_size == 53:
            self.conv0h = nn.Conv2d(dim, dim, kernel_size=(1, 5), stride=(1,1), padding=(0,(5-1)//2), groups=dim)
            self.conv0v = nn.Conv2d(dim, dim, kernel_size=(5, 1), stride=(1,1), padding=((5-1)//2,0), groups=dim)
            self.conv_spatial_h = nn.Conv2d(dim, dim, kernel_size=(1, 17), stride=(1,1), padding=(0,24), groups=dim, dilation=3)
            self.conv_spatial_v = nn.Conv2d(dim, dim, kernel_size=(17, 1), stride=(1,1), padding=(24,0), groups=dim, dilation=3)

        # 通道间卷积，用于融合信息
        self.conv1 = nn.Conv2d(dim, dim, 1)

    # 定义前向传播函数
    def forward(self, x):
        u = x.clone()  # 克隆输入张量
        attn = self.conv0h(x)  # 通过第一个水平卷积层
        attn = self.conv0v(attn)  # 通过第一个垂直卷积层
        attn = self.conv_spatial_h(attn)  # 通过第二个水平卷积层
        attn = self.conv_spatial_v(attn)  # 通过第二个垂直卷积层
        attn = self.conv1(attn)  # 通过1x1卷积层融合信息
        return u * attn  # 输入与注意力权重相乘后返回

实验

脚本

import warnings
warnings.filterwarnings('ignore')
from ultralytics import YOLO
 
if __name__ == '__main__':
	# 修改为自己的配置文件地址
    model = YOLO('./ultralytics/cfg/models/26/yolo26-SPPF_LSKA.yaml')
	# 修改为自己的数据集地址
    model.train(data='./ultralytics/cfg/datasets/coco8.yaml',
                cache=False,
                imgsz=640,
                epochs=10,
                single_cls=False,  # 是否是单类别检测
                batch=8,
                close_mosaic=10,
                workers=0,
                optimizer='MuSGD',  
                # optimizer='SGD',
                amp=False,
                project='runs/train',
                name='yolo26-SPPF_LSKA',
                )

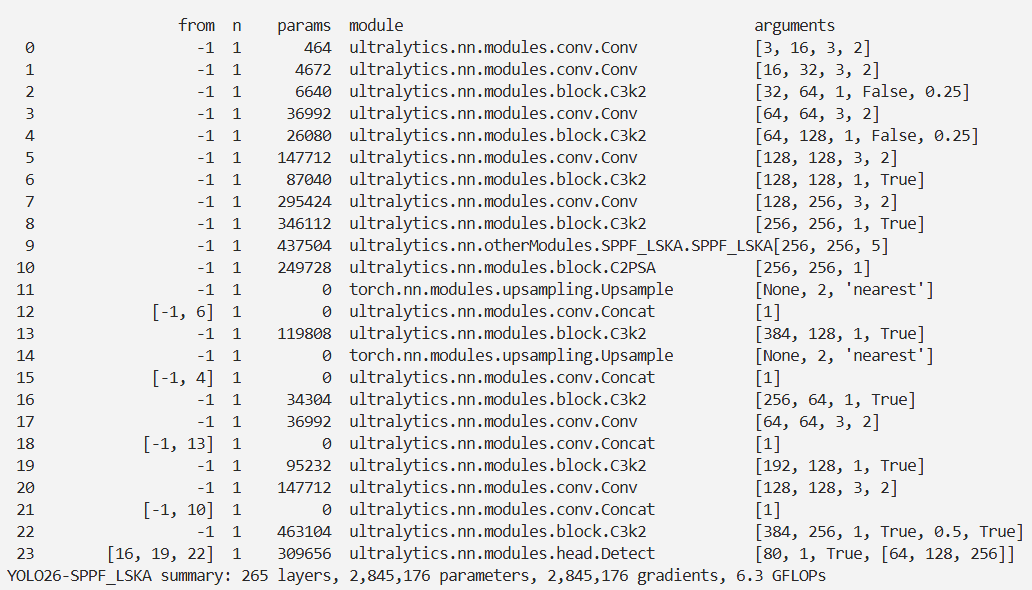
结果

image-20260124213849824

avatar
文章
阅读
粉丝