【MATLAB源码】6G：RIS辅助通信系统 - 建模与优化问题

3GPP仿真实验室
6 阅读2分钟

RIS 辅助 MISO 通信系统：建模与优化问题综述

1. 统一系统模型 (Unified System Model)

本节定义通用的系统架构、信号模型及信道假设。考虑一个由 RIS 辅助的多用户 MISO 下行链路系统。

1.1 节点定义与符号约定

实体描述符号/维度
基站 (BS)配备 MM 根天线，向 KK 个用户发送信息天线数 MM
RIS配备 NN 个无源反射单元单元数 NN
用户 (UE)KK 个单天线用户 (单用户场景下 K=1K=1)用户数 KK

统一符号表：

符号维度物理含义
HBR\mathbf{H}_{BR}N×MN \times MBS 到 RIS 的信道矩阵 (原文档 G\mathbf{G})
hRU,k\mathbf{h}_{RU,k}N×1N \times 1RIS 到用户 kk 的信道向量
hd,k\mathbf{h}_{d,k}M×1M \times 1BS 到用户 kk 的直连信道
Θ\mathbf{\Theta}N×NN \times NRIS 相移对角矩阵 (原文档 Φ\boldsymbol{\Phi})
v\mathbf{v}N×1N \times 1RIS 相移向量，Θ=diag(v)\mathbf{\Theta} = \text{diag}(\mathbf{v})

1.2 信号传输模型

基站向 KK 个用户发送叠加信号 x=∑j=1Kwjsj\mathbf{x} = \sum_{j=1}^{K} \mathbf{w}_j s_j。用户 kk 的接收信号 yky_k 为：

yk=(hd,kH+hRU,kHΘHBR)⏟总等效信道 hkH∑j=1Kwjsj+nky_k = \underbrace{\left( \mathbf{h}_{d,k}^H + \mathbf{h}_{RU,k}^H \mathbf{\Theta} \mathbf{H}_{BR} \right)}_{\text{总等效信道 } \mathbf{h}_k^H} \sum_{j=1}^{K} \mathbf{w}_j s_j + n_k

其中：

  • wj∈CM×1\mathbf{w}_j \in \mathbb{C}^{M \times 1}: 用户 jj 的主动波束赋形向量。
  • sj∼CN(0,1)s_j \sim \mathcal{CN}(0, 1): 发送符号。
  • nk∼CN(0,σ2)n_k \sim \mathcal{CN}(0, \sigma^2): 加性高斯白噪声。

1.3 RIS 反射模型

RIS 的核心是其相移矩阵 Θ\mathbf{\Theta} 和对应的反射系数向量 v\mathbf{v}：

v=[ejθ1,ejθ2,…,ejθN]T\mathbf{v} = [e^{j\theta_1}, e^{j\theta_2}, \ldots, e^{j\theta_N}]^T

关键约束：

  1. 恒模约束 (Unit Modulus): ∣vn∣=1,∀n=1,…,N|v_n| = 1, \forall n=1,\ldots,N。这表示 RIS 仅改变相位，不放大信号（理想无源）。
  2. 相位范围: θn∈[0,2π)\theta_n \in [0, 2\pi)。

1.4 信道衰落模型 (Rician Fading)

考虑到 RIS 通常部署在视距 (LoS) 较好的位置，BS-RIS 信道 HBR\mathbf{H}_{BR} 建模为 Rician 衰落：

HBR=κκ+1HLoS+1κ+1HNLoS\mathbf{H}_{BR} = \sqrt{\frac{\kappa}{\kappa+1}} \mathbf{H}_{\text{LoS}} + \sqrt{\frac{1}{\kappa+1}} \mathbf{H}_{\text{NLoS}}

其中 κ\kappa 为 Rician K 因子，表征 LoS 分量与 NLoS 分量的功率比。

2. 优化场景 A: 多用户加权和速率最大化 (Multi-User WSR)

2.1 性能指标

在多用户干扰信道中，用户 kk 的信干噪比 (SINR) 为：

γk=∣hkHwk∣2∑j≠k∣hkHwj∣2+σ2\gamma_k = \frac{|\mathbf{h}_k^H \mathbf{w}_k|^2}{\sum_{j \neq k} |\mathbf{h}_k^H \mathbf{w}_j|^2 + \sigma^2}

其可达速率为 Rk=log⁡2(1+γk)R_k = \log_2(1 + \gamma_k)。

2.2 问题建模 (P-WSR)

目标是联合设计波束赋形矩阵 W\mathbf{W} 和 RIS 相位 v\mathbf{v} 以最大化加权和速率：

max⁡W,v∑k=1KωkRks.t.∑k=1K∥wk∥2≤Pmax⁡(BS 功率约束)∣vn∣=1,∀n=1,…,N(RIS 恒模约束)\begin{aligned} \max_{\mathbf{W}, \mathbf{v}} \quad & \sum_{k=1}^{K} \omega_k R_k \\ \text{s.t.} \quad & \sum_{k=1}^{K} \|\mathbf{w}_k\|^2 \leq P_{\max} \quad \text{(BS 功率约束)} \\ & |v_n| = 1, \quad \forall n = 1, \ldots, N \quad \text{(RIS 恒模约束)} \end{aligned}

2.3 难点分析

  • 目标函数复杂: 和速率函数对于 (W,v)(\mathbf{W}, \mathbf{v}) 是非凸的。
  • 变量耦合: 信号在信道中经历了 W\mathbf{W} 和 Θ\mathbf{\Theta} 的双重作用。
  • 求解策略: 通常采用 交替优化 (AO) 或 加权最小均方误差 (WMMSE) 算法。

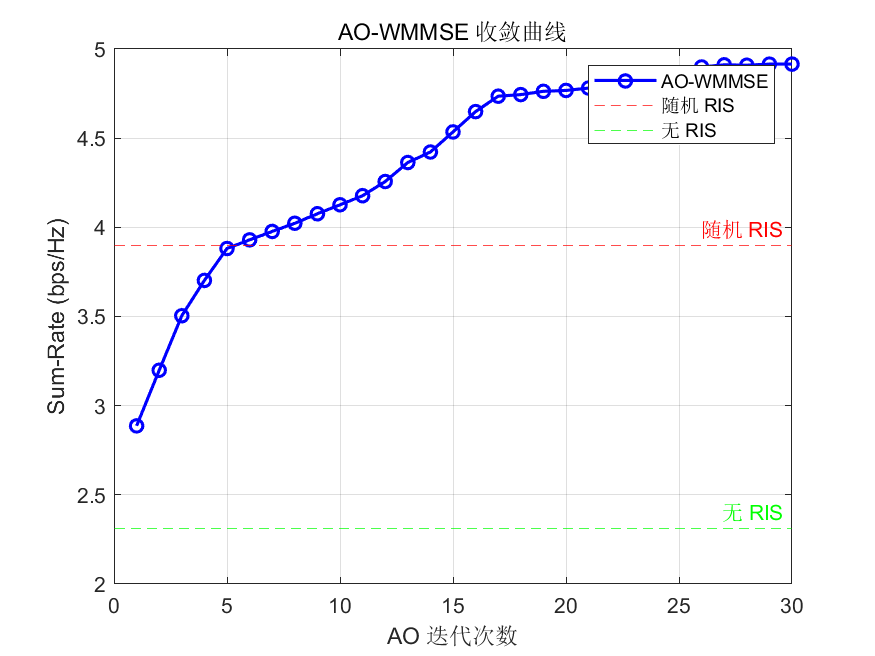
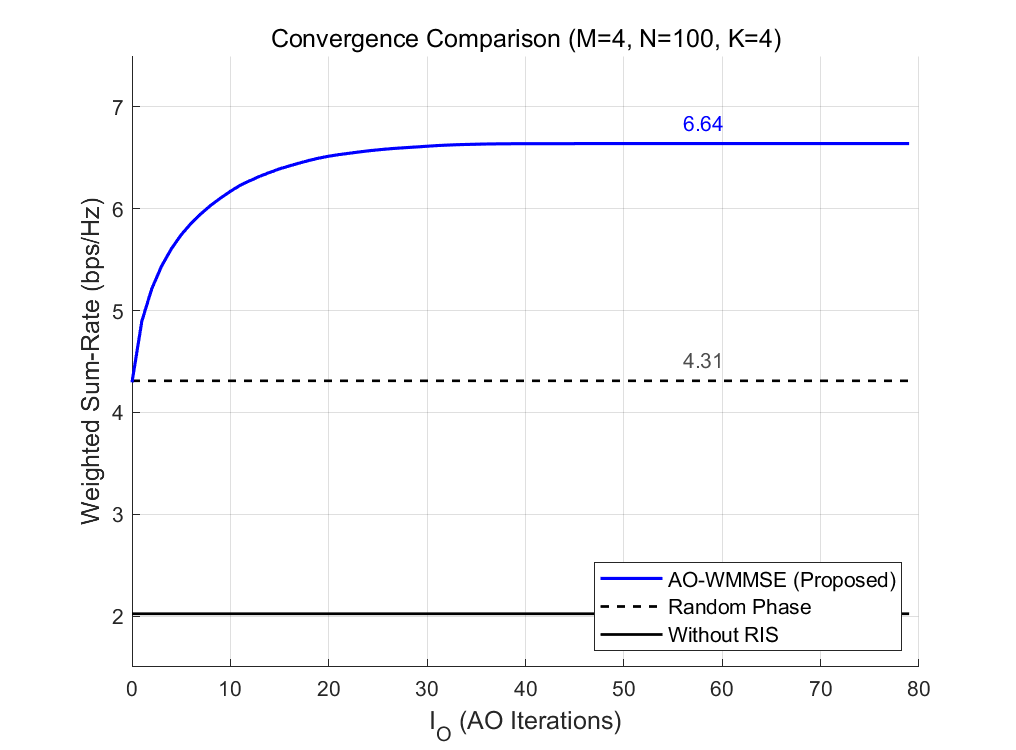
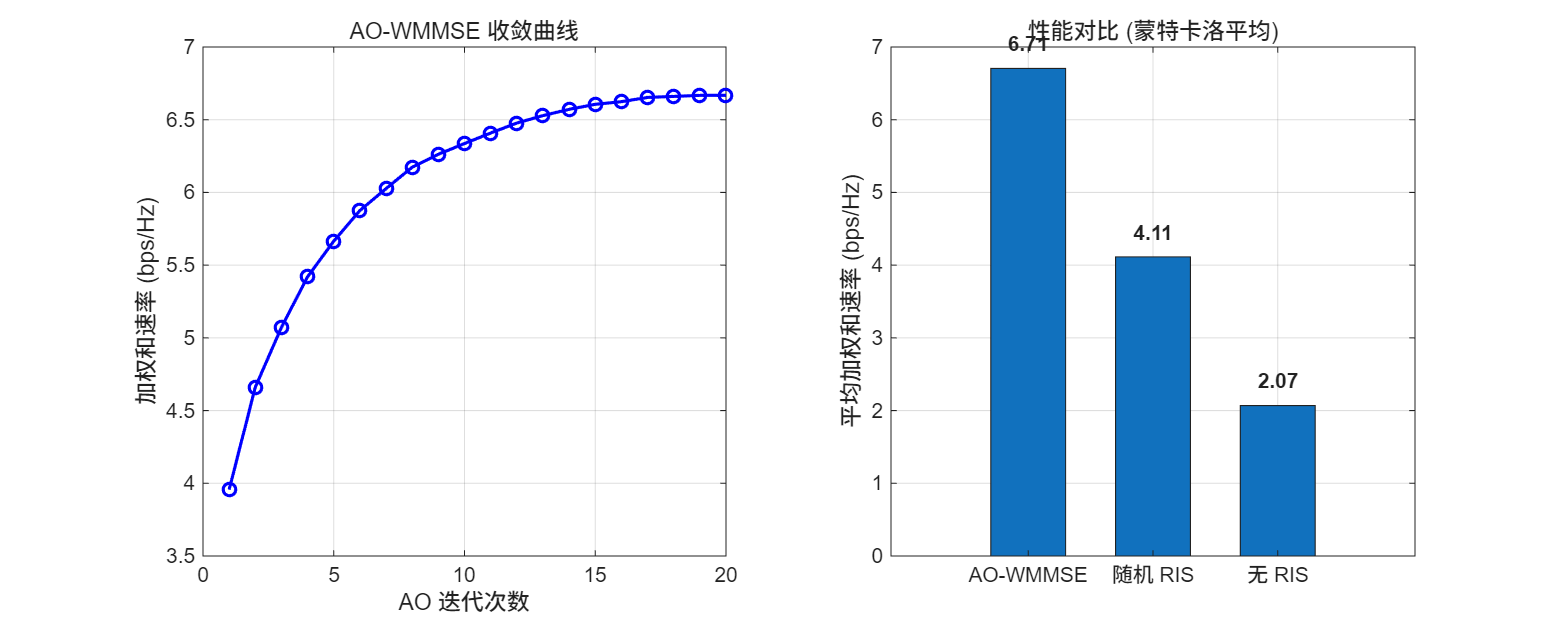
convergence_test.png fig4_reproduction.png sum_rate_comparison.png

3. 优化场景 B: 单用户联合波束赋形 (Joint Beamforming)

当 K=1K=1 时，干扰项消失，问题退化为最大化点对点链路的 SNR。

3.1 等效信道与级联信道

利用恒等式 aHdiag(v)B=vT(diag(aH)B)\mathbf{a}^H \text{diag}(\mathbf{v}) \mathbf{B} = \mathbf{v}^T (\text{diag}(\mathbf{a}^H)\mathbf{B})，可定义等效信道 heff\mathbf{h}_{eff}：

heff(v)=hd+HBRHdiag(v)hRU=hd+HBRH(v⊙hRU)\mathbf{h}_{eff}(\mathbf{v}) = \mathbf{h}_d + \mathbf{H}_{BR}^H \text{diag}(\mathbf{v}) \mathbf{h}_{RU} = \mathbf{h}_d + \mathbf{H}_{BR}^H (\mathbf{v} \odot \mathbf{h}_{RU})

3.2 优化问题 (P-SNR)

max⁡w,vlog⁡2(1+∣heff(v)Hw∣2σ2)s.t.∥w∥2≤Pmax,∣vn∣=1\begin{aligned} \max_{\mathbf{w}, \mathbf{v}} \quad & \log_2 \left( 1 + \frac{|\mathbf{h}_{eff}(\mathbf{v})^H \mathbf{w}|^2}{\sigma^2} \right) \\ \text{s.t.} \quad & \|\mathbf{w}\|^2 \leq P_{max}, \quad |v_n| = 1 \end{aligned}

[!NOTE]

对于固定的 v\mathbf{v}，最优波束赋形 w∗\mathbf{w}^* 是最大比传输 (MRT)：w∗=Pmaxheff∥heff∥\mathbf{w}^* = \sqrt{P_{max}} \frac{\mathbf{h}_{eff}}{\|\mathbf{h}_{eff}\|}。这允许我们将问题简化为仅针对 v\mathbf{v} 的优化。

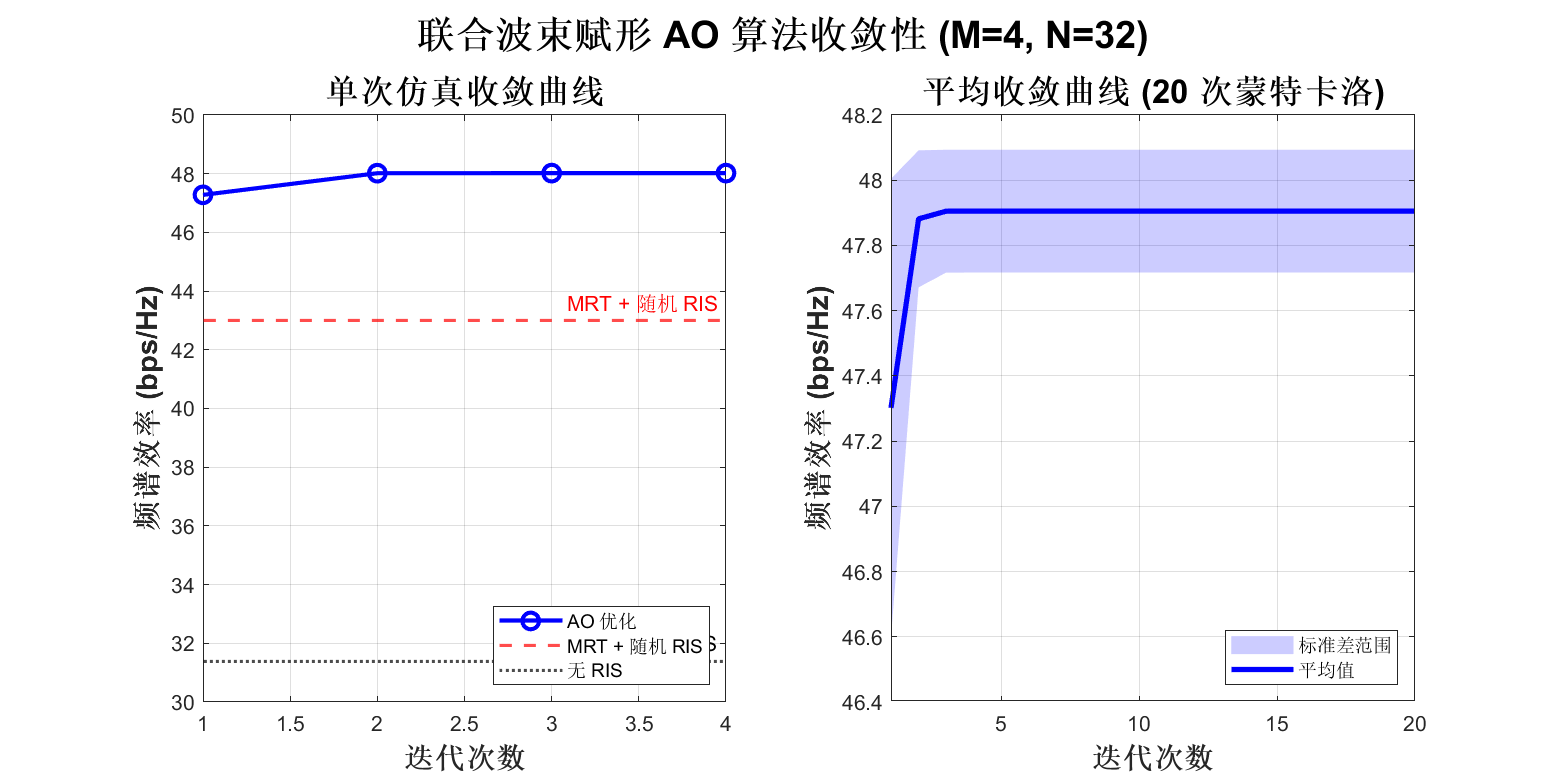
convergence_curve.png

4. 优化场景 C: RIS 无源波束赋形 (Passive Beamforming Only)

假设直连链路被阻挡 (hd≈0\mathbf{h}_d \approx 0) 且 BS 端波束赋形固定（或单天线），系统退化为仅通过 RIS 最大化接收功率。

4.1 级联信道模型

定义级联信道向量 hcas=hRU∗⊙hBR\mathbf{h}_{cas} = \mathbf{h}_{RU}^* \odot \mathbf{h}_{BR} (其中 hBR\mathbf{h}_{BR} 退化为 N×1N \times 1 向量)。目标函数转化为二次型形式：

∣hRUHΘhBR∣2=∣vHhcas∣2=vHhcashcasHv|\mathbf{h}_{RU}^H \mathbf{\Theta} \mathbf{h}_{BR}|^2 = |\mathbf{v}^H \mathbf{h}_{cas}|^2 = \mathbf{v}^H \mathbf{h}_{cas} \mathbf{h}_{cas}^H \mathbf{v}

令 R=hcashcasH\mathbf{R} = \mathbf{h}_{cas} \mathbf{h}_{cas}^H，问题转化为非凸二次约束二次规划 (QCQP)：

4.2 优化问题 (P-QCQP)

max⁡vvHRvs.t.∣vn∣=1,∀n=1,…,N\begin{aligned} \max_{\mathbf{v}} \quad & \mathbf{v}^H \mathbf{R} \mathbf{v} \\ \text{s.t.} \quad & |v_n| = 1, \quad \forall n = 1, \dots, N \end{aligned}

4.3 求解方法

  • 半正定松弛 (SDR): 将 vvH\mathbf{v}\mathbf{v}^H 提升为矩阵 V\mathbf{V}，忽略秩为 1 的约束求解，最后通过高斯随机化恢复 v\mathbf{v}。
  • 流形优化 (Manifold Optimization): 直接在复圆流形 (Complex Circle Manifold) 上进行梯度下降。

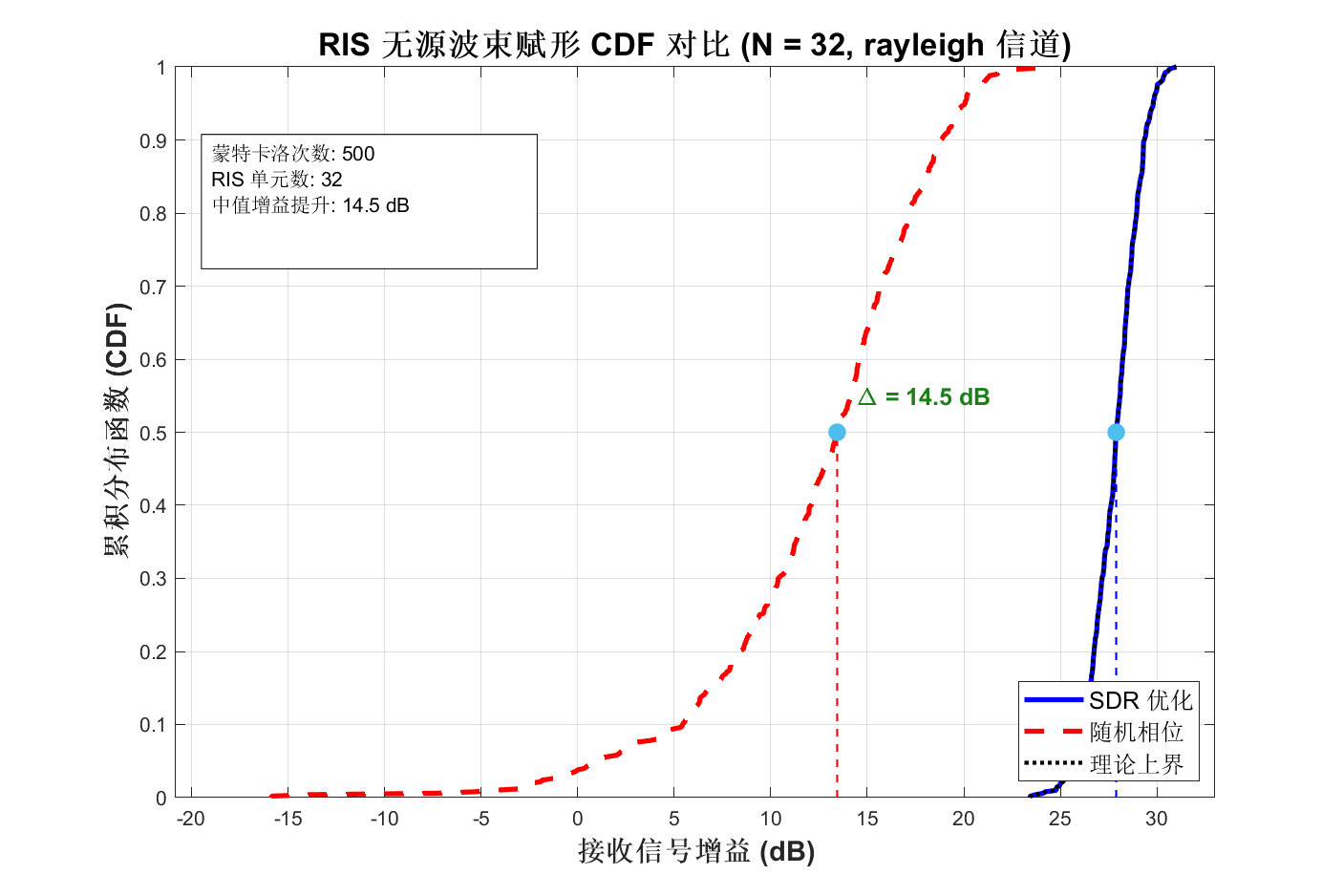
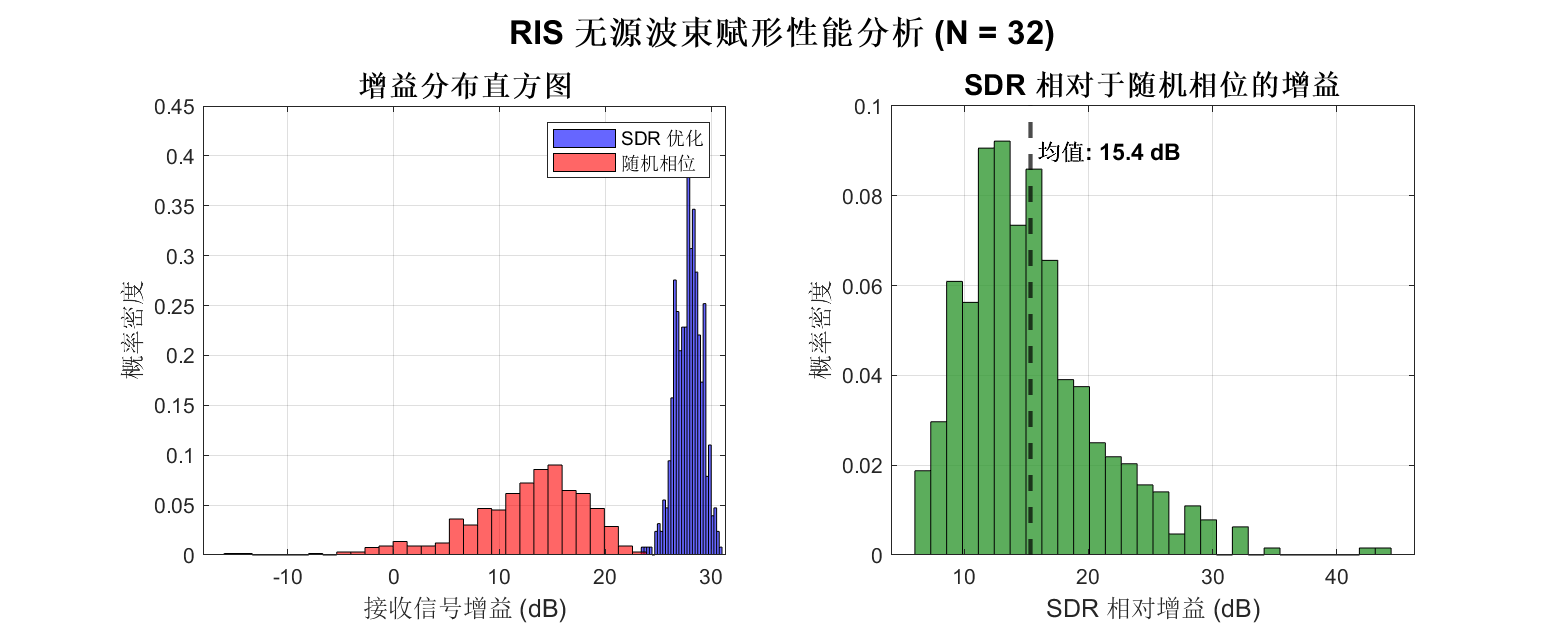
cdf_comparison.pnggain_distribution.png

5. 总结与复杂度分析

所有上述问题均属于 非凸优化问题 (Non-convex Optimization)，主要困难来源于：

  1. 恒模约束: ∣vn∣=1|v_n|=1 构成的可行域是环形流形，而非凸集。
  2. 变量耦合: 在联合设计中，w\mathbf{w} 与 v\mathbf{v} 乘积耦合。

[!IMPORTANT]

NP-hard 性质: 一般情况下，寻找全局最优解是 NP-hard 的。实际工程实现通常寻求高质量的次优解（局部最优）。

🛒 获取

本文代码仅为核心片段，完整版工程已整理好。 关注公众号 【3GPP仿真实验室】进行获取。

avatar
文章
阅读
粉丝