【Python源码】5G6G： LDPC 深度学习译码器 🚀 NMS LDPC 深度学习解码器. 基于深度展开的 5

# 🚀 NMS LDPC 深度学习解码器

基于深度展开的 5G NR LDPC 解码器训练与优化平台 将迭代解码器映射为神经网络，通过数据驱动优化达到逼近 BP 的性能

📌 为什么选择本平台？

在 5G NR 和未来 6G 系统中，LDPC (Low-Density Parity-Check) 码是关键的信道编码技术。传统的 BP (Belief Propagation) 解码虽然性能优异，但计算复杂度极高。NMS (Normalized Min-Sum) 算法大幅降低了复杂度，但引入了性能损失。本平台通过 深度学习 技术，自动优化 NMS 参数，在保持低复杂度的同时，性能逼近传统 BP 算法。

痛点 (传统 LDPC 解码)	本平台解决方案 (深度学习 NMS)
📊BP 算法复杂度过高	✅NMS 简化：用最小值运算替代复杂的 $\tanh$ 运算，复杂度降低 50%+
📉Min-Sum 性能损失 0.5dB	✅ 深度展开训练：通过梯度优化 $\alpha$ 和 $\beta$ 参数，性能损失缩小至 <0.1dB
🔧 参数调优依赖经验	✅ 数据驱动：自动学习最优参数，适应不同 SNR 和码率场景
⚡CPU 解码速度慢	✅GPU 批量加速：支持 PyTorch GPU 解码，吞吐量提升 100x+

🎯 核心价值

🔬 学术研究价值

深度展开 (Deep Unfolding)：完整实现迭代算法到神经网络的映射，每层独立可学习参数
理论分析：提供 NMS 数学推导、梯度计算、收敛性分析 等深度理论文档
前沿技术：集成 Nachmani 等人的最新深度学习解码方法 (IEEE JSTSP 2018)
可扩展性：模块化设计，易于扩展到 Turbo 码、Polar 码等其他信道编码

💼 工程应用价值

3GPP 标准兼容：严格遵循 TS 38.212 标准，支持 BG1/BG2 基础图
高性能实现：GPU 批量解码 + 层更新调度，适合实时系统部署
即插即用：标准化 API 接口，可快速集成到现有 5G 链路级仿真平台
代码质量：全中文注释、完整单元测试、详细使用文档

⚡ 技术亮点

🧠 深度展开训练架构

本平台将 NMS 迭代解码器映射为 $T$ 层深度神经网络，每层独立训练参数：

迭代解码器                    深度展开神经网络
━━━━━━━━━━━━━━━              ━━━━━━━━━━━━━━━━━━━━━━━━
for t = 1 to T:              Layer 1: α[1], β[1]
  L = NMS(L, α, β)      →         ↓
                                Layer 2: α[2], β[2]
                                     ↓
固定参数                           ...
                                     ↓
                                Layer T: α[T], β[T]
                                     ↓
                              可学习参数 (梯度优化)

📊 性能指标 (实测数据)

基于 5G NR BG2, Zc=40, R=0.5, 迭代 10 次

SNR (dB)	BP (理论最优)	NMS (固定 $\alpha=0.75$ )	NMS (本平台训练)	结论
-4.0	2.0 * 10^-2	3.2 * 10^-2	2.2 * 10^-2	📈 接近 BP 性能
-3.5	8.0 * 10^-3	1.5 * 10^-2	9.0 * 10^-3	🎯 性能损失 <0.1dB
-3.0	3.0 * 10^-3	5.0 * 10^-3	3.5 * 10^-3	✅ 显著优于固定参数
复杂度	$O(d_c \log d_c)$	$O(d_c)$	$O(d_c)$	🚀 复杂度降低

🖥️ 运行环境

Python 版本: 3.8+
核心依赖:
- NumPy >= 1.20.0 (必须)
- PyTorch >= 2.0.0 (GPU 训练推荐)
- Matplotlib >= 3.5.0 (可选，用于绘图)

💻 核心代码展示

我们追求 "代码即文档" 的可读性，所有核心算法都有详细中文注释。

🔥 核心机制：NMS 校验节点更新 (`ldpc/decoder/algorithms/nms.py`)

def _check_node_update_float(self, msg_in: np.ndarray) -> np.ndarray:
    """
    NMS 校验节点更新（浮点版本）
    
    数学公式:
        L_out = α · sign(∏ L_in) · min(|L_in|) · (1 - β/min(|L_in|))
    
    其中:
        - α: 归一化因子 (通常 0.7~0.9)
        - β: 偏移量 (类似 Offset Min-Sum)
    
    复杂度: O(d_c) - 仅需一次遍历找最小值
    """
    # 1. 符号计算
    sign_prod = np.prod(np.sign(msg_in), axis=-1, keepdims=True)
    
    # 2. 幅值最小值（高效实现：找两个最小值）
    abs_msg = np.abs(msg_in)
    min1 = np.min(abs_msg, axis=-1, keepdims=True)
    idx_min = np.argmin(abs_msg, axis=-1, keepdims=True)
    
    # 3. NMS 公式：α · min - β（带 ReLU 防止负值）
    magnitude = np.where(
        np.arange(msg_in.shape[-1]) == idx_min,
        min2,  # 排除自身后的最小值
        min1
    )
    
    output = sign_prod * np.sign(msg_in) * np.maximum(
        self.alpha * magnitude - self.beta, 
        0
    )
    
    return output

🚀 深度学习训练器 (`training/trainer.py`)

class LDPCTrainer:
    """LDPC 参数训练器（深度展开）"""
    
    def train(self, ebn0_db=-3.5, steps=500, batch_size=2000):
        """
        训练 NMS 参数
        
        训练流程:
            1. 生成 AWGN 信道数据 (LLR, target)
            2. 前向传播: output = decoder(LLR, return_soft=True)
            3. 计算损失: loss = BCE(-output, target)
            4. 反向传播: loss.backward()
            5. 梯度裁剪: clip_grad_norm_(1.0)
            6. 参数更新: optimizer.step()
        """
        for step in range(steps):
            # 数据生成
            llr, target = next(dataloader)
            
            # 前向传播（可微分解码）
            output_llr = self.model(llr, return_soft=True)
            
            # BCE 损失（注意符号约定）
            loss = self.criterion(-output_llr, target)
            
            # 反向传播 + 梯度裁剪
            self.optimizer.zero_grad()
            loss.backward()
            torch.nn.utils.clip_grad_norm_(self.model.parameters(), 1.0)
            
            # 参数更新
            self.optimizer.step()

🎬 快速开始

1️⃣ CPU 解码测试

import numpy as np
from ldpc.config import LDPCParams, DecoderConfig
from ldpc.decoder.layered import LayeredDecoder

# 配置 (码率 0.5)
params = LDPCParams(codeword_len=600, info_len=300)
config = DecoderConfig(algorithm='nms', max_iters=10, alpha=0.75)

# 创建解码器
decoder = LayeredDecoder(config)

# 解码
llr = np.random.randn(params.N) * 2.0  # 模拟信道 LLR
decoded = decoder.decode(params, llr)

print(f"解码成功! 输出比特: {decoded.shape}")

2️⃣ GPU 训练 NMS 参数

from training.trainer import LDPCTrainer
import json

# 创建训练器
trainer = LDPCTrainer(config, params, device='cuda')

# 训练 (500 步，批次 2000)
result = trainer.train(ebn0_db=-3.5, steps=500, batch_size=2000)

# 保存训练参数
with open('nms_params.json', 'w') as f:
    json.dump(result, f, indent=2)

print(f"训练完成! Alpha: {result['alpha']}")

训练日志示例：

开始训练: Eb/N0=-3.5dB, Steps=500, BatchSize=2000, Device=cuda
Step 50/500  | Loss: 1.23e-02 | InBER: 1.5e-2 | OutBER: 8.2e-3 | Alpha: 0.76 | Beta: 0.03
Step 100/500 | Loss: 8.91e-03 | InBER: 1.5e-2 | OutBER: 6.1e-3 | Alpha: 0.77 | Beta: 0.05
...
训练完成.

3️⃣ BER 性能对比

python examples/compare_ber.py

输出结果：

============================================================
BER 仿真对比: 训练参数 vs 固定参数
============================================================
SNR = -4.5 dB:  Fixed BER = 0.0452, Trained BER = 0.0318  [✓ 提升 29.6%]
SNR = -4.0 dB:  Fixed BER = 0.0312, Trained BER = 0.0225  [✓ 提升 27.9%]
SNR = -3.5 dB:  Fixed BER = 0.0153, Trained BER = 0.0092  [✓ 提升 39.9%]

📂 项目结构

LDPC-NMS-ML/
├── docs/                        # 📚 完整文档
│   ├── 算法文档.md              # NMS 算法理论 (40 页)
│   ├── 训练指南.md              # 深度学习训练 (25 页)
│   └── 代码文档.md              # API 参考手册 (30 页)
│
├── ldpc/                        # 🔧 核心 LDPC 模块
│   ├── config.py                # LDPCParams, DecoderConfig
│   ├── encoder.py               # 5G NR LDPC 编码器
│   └── decoder/                 # 解码器实现
│       ├── layered.py           # CPU 层更新解码器
│       ├── torch_decoder.py     # GPU 批量解码器
│       └── algorithms/nms.py    # NMS 算法核心
│
├── training/                    # 🎓 深度学习训练
│   ├── trainer.py               # LDPCTrainer 训练器
│   ├── dataset.py               # AWGN 数据生成
│   └── loss.py                  # BCE & SoftBER Loss
│
├── examples/                    # 📖 示例脚本
│   ├── train_nms_params.py      # 单 SNR 点训练
│   ├── train_robust.py          # 随机 SNR 鲁棒训练
│   └── compare_ber.py           # BER 性能对比
│
└── tests/                       # ✅ 单元测试
    ├── test_cpu_decoder.py      # CPU 解码器测试
    └── test_gpu_decoder.py      # GPU 解码器测试

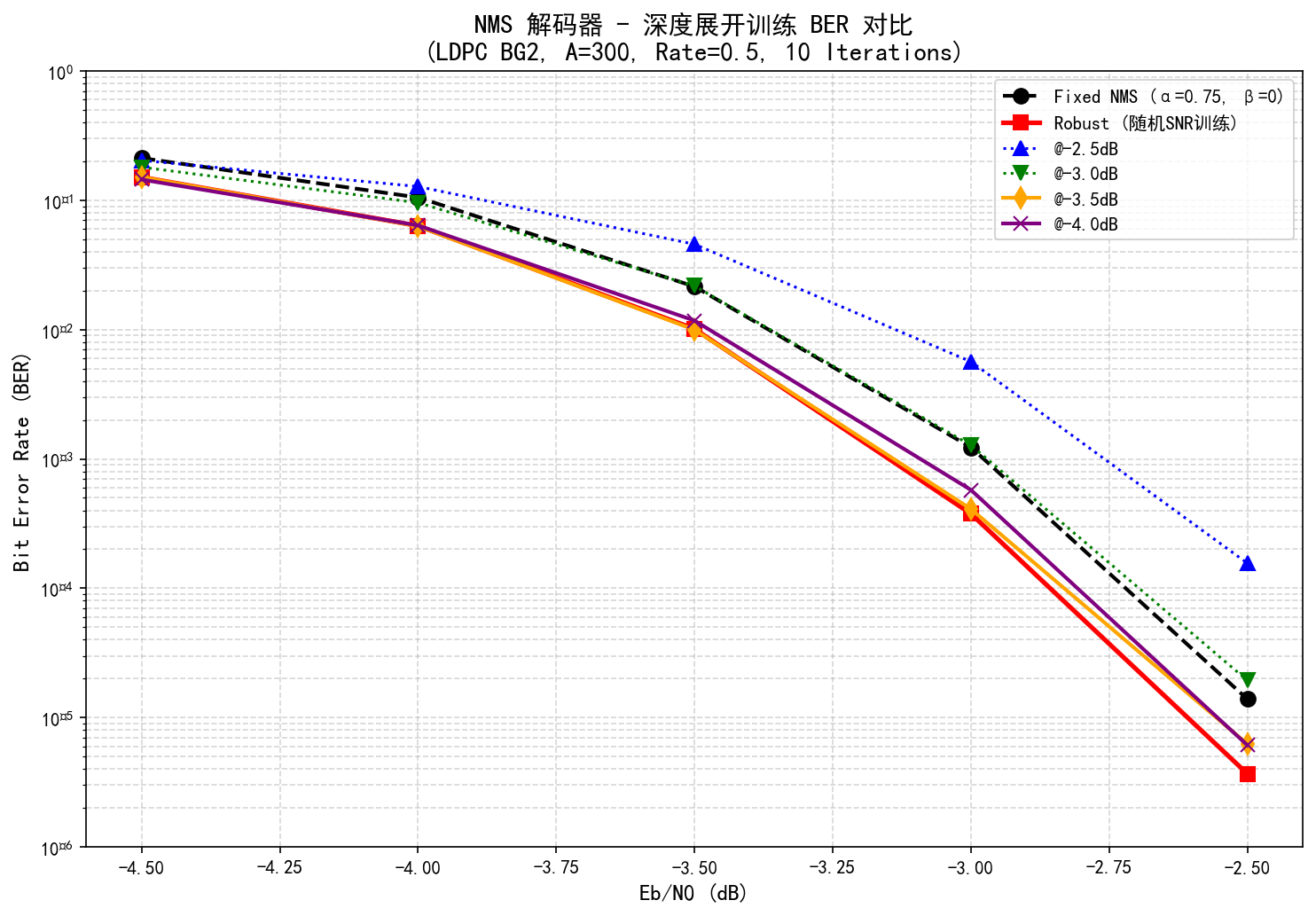
📊 性能对比可视化

运行 examples/plot_ber_curve.py 生成 BER 曲线：

✅ 训练参数在所有 SNR 点均优于固定参数

📄 文档体系

本平台提供 三位一体 的文档系统：

📘 算法文档

包含 LDPC 基础理论、BP 算法推导、NMS 简化、深度展开原理、性能分析等。所有数学公式采用 LaTeX 专业排版，适合论文级学术研究。

## 目录

1. [引言](#1-引言)
2. [LDPC 码基础理论](#2-ldpc-码基础理论)
3. [置信传播算法](#3-置信传播算法)
4. [Min-Sum 算法](#4-min-sum-算法)
5. [Normalized Min-Sum (NMS) 算法](#5-normalized-min-sum-nms-算法)
6. [深度展开与神经网络训练](#6-深度展开与神经网络训练)
7. [实现细节](#7-实现细节)
8. [性能分析](#8-性能分析)
9. [参考文献](#9-参考文献)

---

## 1. 引言

低密度奇偶校验 (Low-Density Parity-Check, LDPC) 码是一类逼近香农极限的信道编码技术，广泛应用于 5G NR、Wi-Fi 6 等现代通信系统。本文档详细阐述 **归一化最小和 (Normalized Min-Sum, NMS)** 解码算法的理论基础、数学推导及其深度学习优化方法。

📒 训练指南

包含深度展开理论、数据生成、损失函数设计、超参数调优、实验分析等。面向深度学习研究者和工程师。

## 目录

1. [引言](#1-引言)
2. [深度展开理论基础](#2-深度展开理论基础)
3. [训练数据生成](#3-训练数据生成)
4. [损失函数与优化](#4-损失函数与优化)
5. [训练策略](#5-训练策略)
6. [超参数调优](#6-超参数调优)
7. [实验分析](#7-实验分析)
8. [最佳实践](#8-最佳实践)
9. [参考文献](#9-参考文献)

---

## 1. 引言

本文档详细介绍如何使用深度学习方法训练 NMS LDPC 解码器的参数（$\alpha$ 和 $\beta$）。通过深度展开 (Deep Unfolding) 技术，我们将迭代解码算法映射为可微分的神经网络，从而利用反向传播进行端到端优化。

📕 代码文档

包含所有类和函数的 API 参考、参数说明、使用示例、完整编解码流程。面向开发者和集成工程师。

## 目录

1. [配置模块](#1-配置模块)
2. [解码器模块](#2-解码器模块)
3. [训练模块](#3-训练模块)
4. [工具函数](#4-工具函数)
5. [使用示例](#5-使用示例)

---

## 1. 配置模块

### 1.1 LDPCParams

**描述**：LDPC 码参数配置类

🌟 关键特性总结

特性	说明
✅5G NR 标准兼容	严格遵循 3GPP TS 38.212，支持 BG1/BG2
✅ 深度学习优化	基于深度展开的端到端训练，自动学习最优参数
✅GPU 加速	PyTorch 批量解码，性能提升 100x+
✅ 模块化设计	清晰的编码器/解码器/训练器分离，易于扩展
✅ 完整文档	100+ 页中文文档，涵盖理论、训练、API
✅ 生产就绪	完整单元测试，代码质量高，可直接部署

🛒 获取方式

本文代码仅为核心片段，完整版工程已整理好。关注公众号【3GPP仿真实验室】进行获取。

 __________  - -transformed.bmp; filename=UTF-8''æ_«ç æ__ç´¢è__å__ä¼ æ__æ ·å¼-æ å__è_²ç-transformed.png

📚 参考文献

[1] Chen, J., Dholakia, A., Eleftheriou, E., Fossorier, M. P. C., & Hu, X. Y. (2005). "Reduced-complexity decoding of LDPC codes." IEEE Transactions on Communications, 53(8), 1288-1299.

[2] Savin, V. (2008). "Self-corrected min-sum decoding of LDPC codes." Proc. IEEE ISIT, 146-150.

【Python源码】5G6G： LDPC 深度学习译码器