【MATLAB源码】5G： LDPC 教科书级编解码仿真平台

​

📡 5G NR LDPC 教科书级编解码仿真平台

3GPP TS 38.212 协议逐行复现 · 工业级代码规范 支持 NMS/OMS/SP 三大译码算法 · 层更新架构 · 完整收发链路

​

📌 为什么选择本仿真平台？

对着 3GPP TS 38.212 文档发愁？满屏的 Zc 表格、移位系数、双对角编码流程让人头大？网上找的代码变量名乱写、跑不出正确的 BER 曲线？

本平台提供了一套 教科书级 的 5G NR LDPC 全链路实现，每一行代码都严格对应协议章节。

痛点 (网上代码)	本平台解决方案
🔴 变量命名混乱(temp, data1, xx)	✅3GPP 标准命名：A, K, Zc, n_F, BGn... 与协议一一对应
🔴 代码和公式对不上	✅ 逐行中文注释：[Section 5.3.2] 精确标注协议章节
🔴 缺少速率匹配/恢复模块	✅ 全链路闭环：缩短 → 打孔 → 循环缓冲 → 逆操作，完整实现
🔴 译码性能差，画不出瀑布曲线	✅ 工业级译码器：层更新调度 + 双重早停机制，BER 正确收敛
🔴 只有单一算法，无法对比	✅ 三大算法并行：NMS/OMS/SP 即插即用，一键生成对比曲线

🎯 核心价值

​​

🔬 学术研究价值

• 协议复现：完整实现 TS 38.212 Section 5.1~5.4 全流程
• 算法对比：NMS/OMS/SP 三种校验节点更新算法
• 公式对应：代码注释直接引用 3GPP 公式编号
• 教学友好：demo_ldpc_e2e.m 演示完整收发链路

💼 工程应用价值

• 模块解耦：Encoder/Decoder/RateMatch 独立模块
• 性能验证：BER/FER 曲线符合理论预期
• 易于扩展：可集成到现有 5G 链路级仿真
• 代码质量：全中文注释，适合团队协作

⚡ 技术亮点

🏗️ 完整模块架构

matlab/
├── 【3GPP 标准表格】
│   └── nrLDPCTables.m         # 完整移位系数 (BG1: 316条边, BG2: 197条边)
│
├── 【发端模块】
│   ├── nrLDPCParams.m         # [Section 5.2.2, 6.2.2] 参数计算 + BG选择
│   ├── nrLDPCSegment.m        # [Section 5.2.2] 码块分割 + CRC
│   ├── nrLDPCEncode.m         # [Section 5.3.2] 双对角 LDPC 编码
│   └── nrLDPCRateMatch.m      # [Section 5.4.2] 缩短+打孔+循环缓冲
│
├── 【收端模块】
│   ├── nrLDPCRateRecover.m    # 速率恢复 (逆操作)
│   ├── nrLDPCDecode.m         # 层更新译码器 (支持 NMS/OMS/SP)
│   └── nrLDPCDesegment.m      # 码块合并 + CRC 校验
│
├── 【译码算法】
│   ├── nms_check_node_update.m   # 归一化最小和 (α=0.75)
│   ├── oms_check_node_update.m   # 偏移最小和 (β=0.15)
│   └── sp_check_node_update.m    # 和积算法 (理论最优)
│
└── 【测试与仿真】
    ├── demo_ldpc_e2e.m            # 🔥 完整链路演示 (含 3GPP 流程图)
    ├── sim_algorithm_comparison.m # NMS/OMS/SP 性能对比
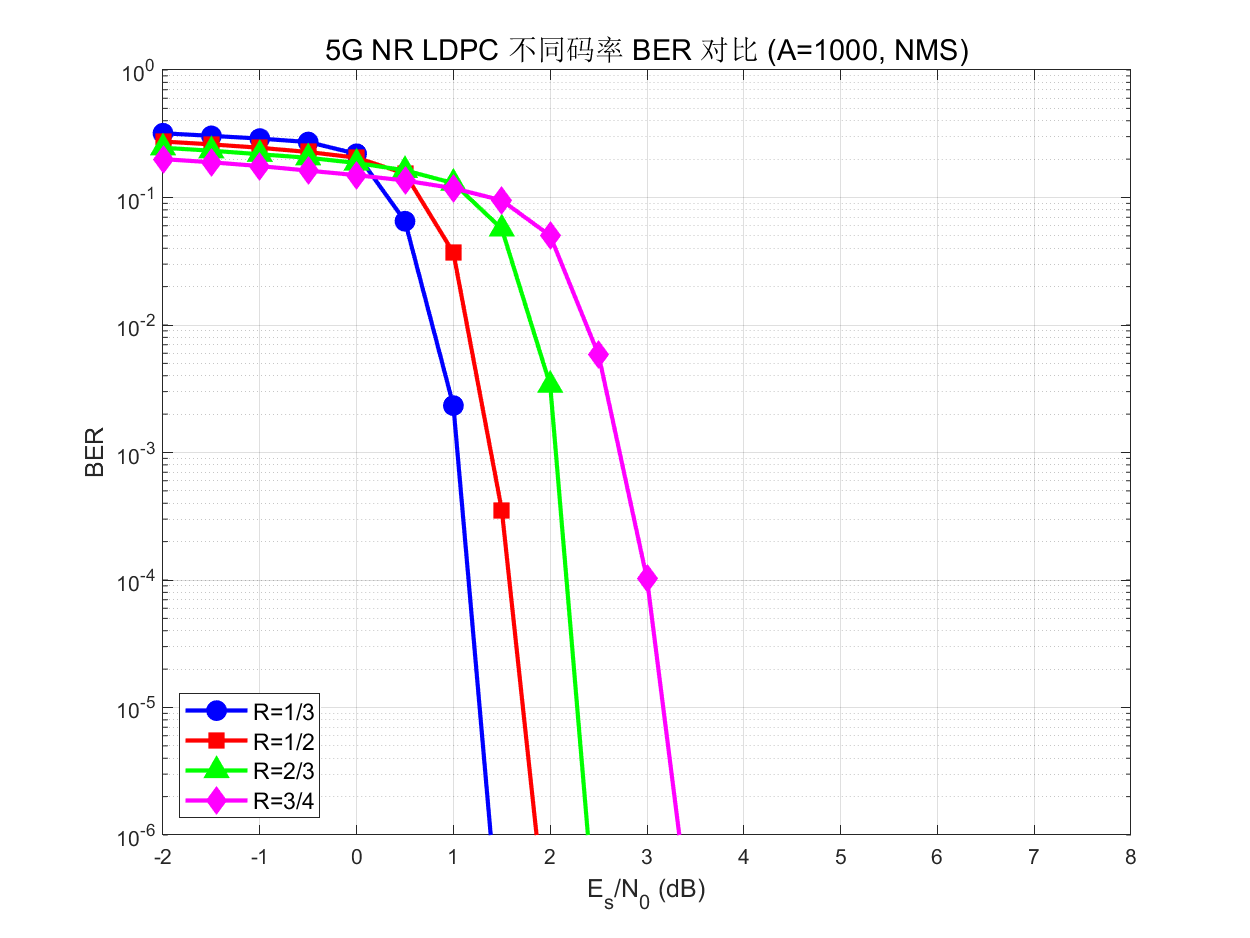
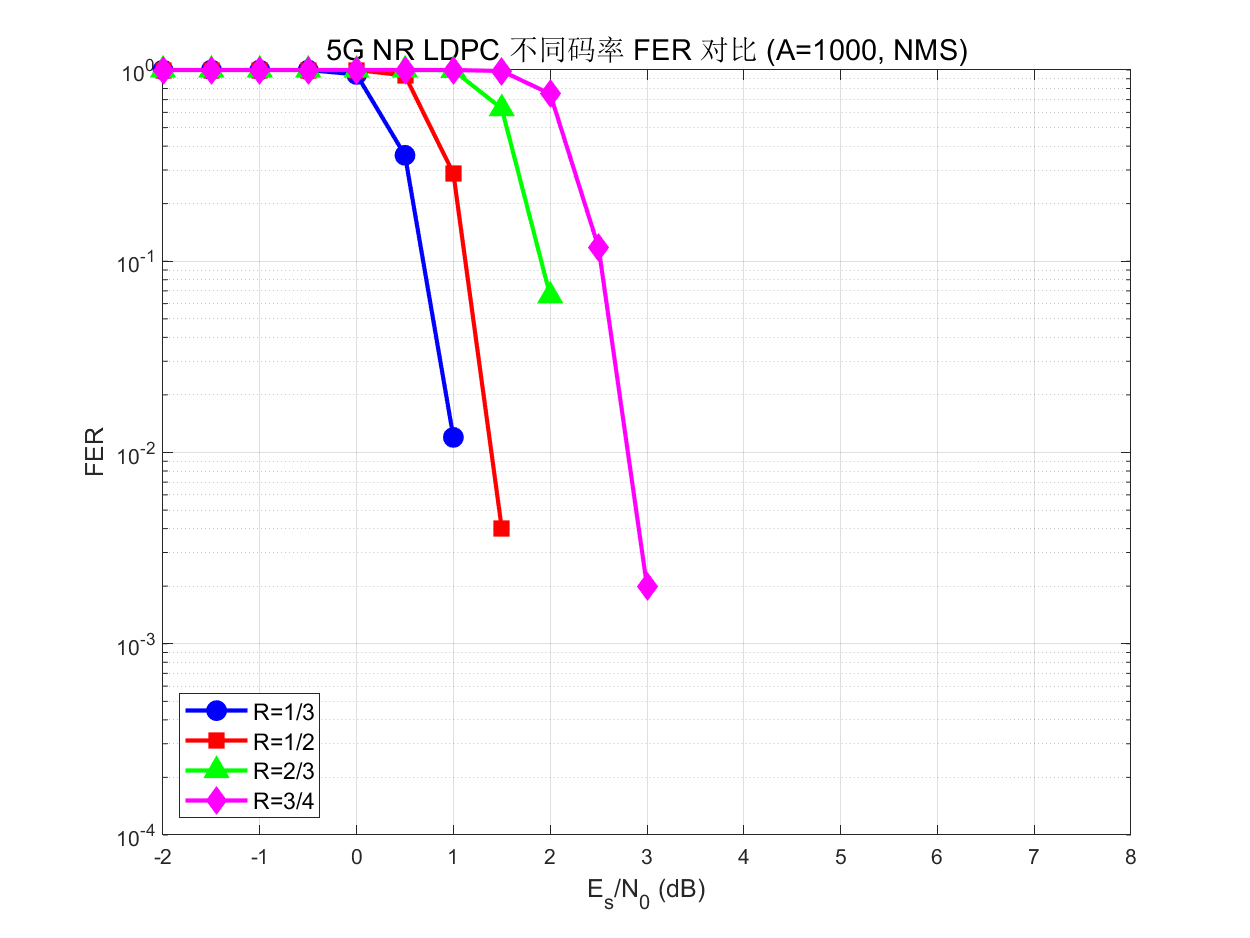
    └── sim_code_rate_comparison.m # 不同码率 BER 曲线

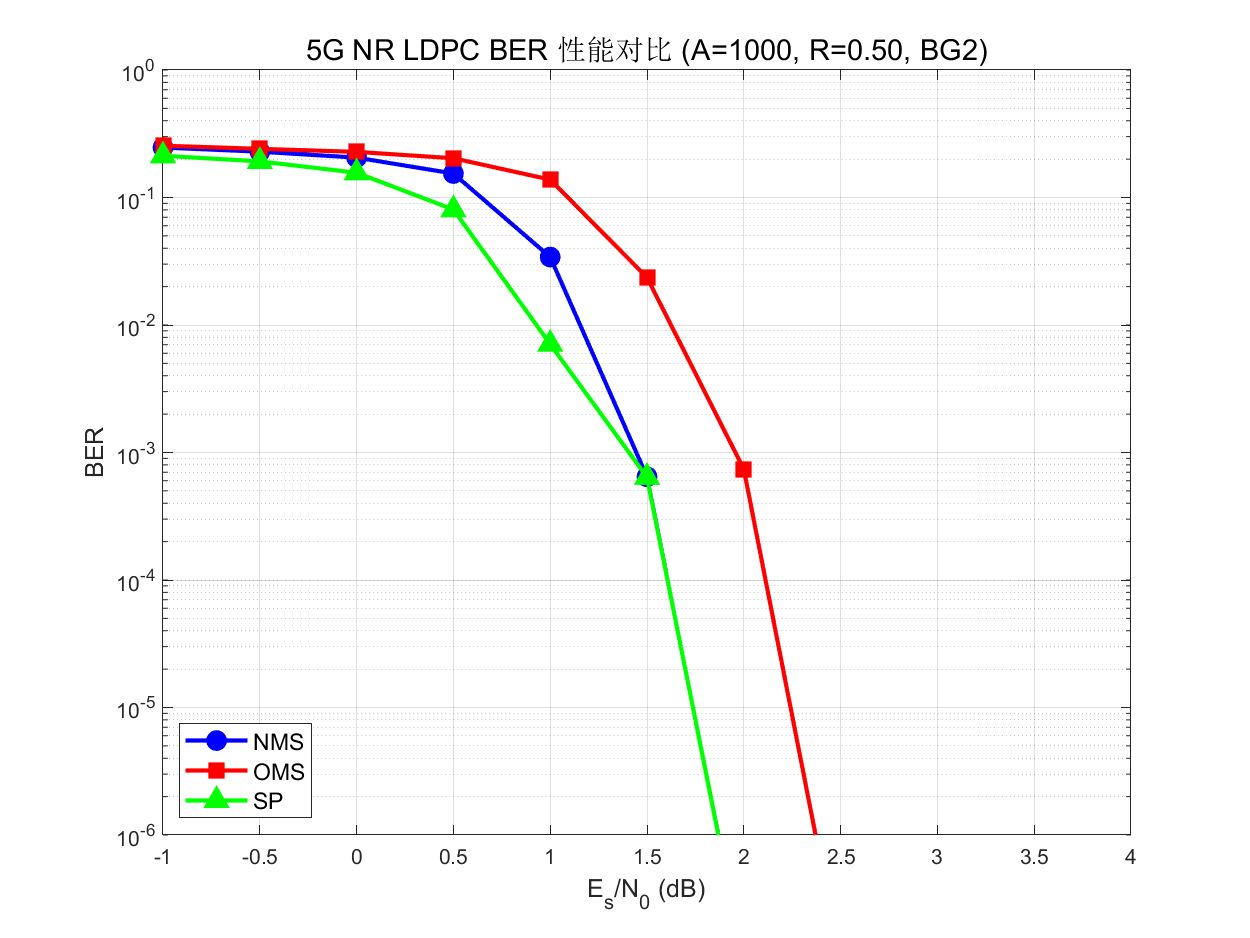
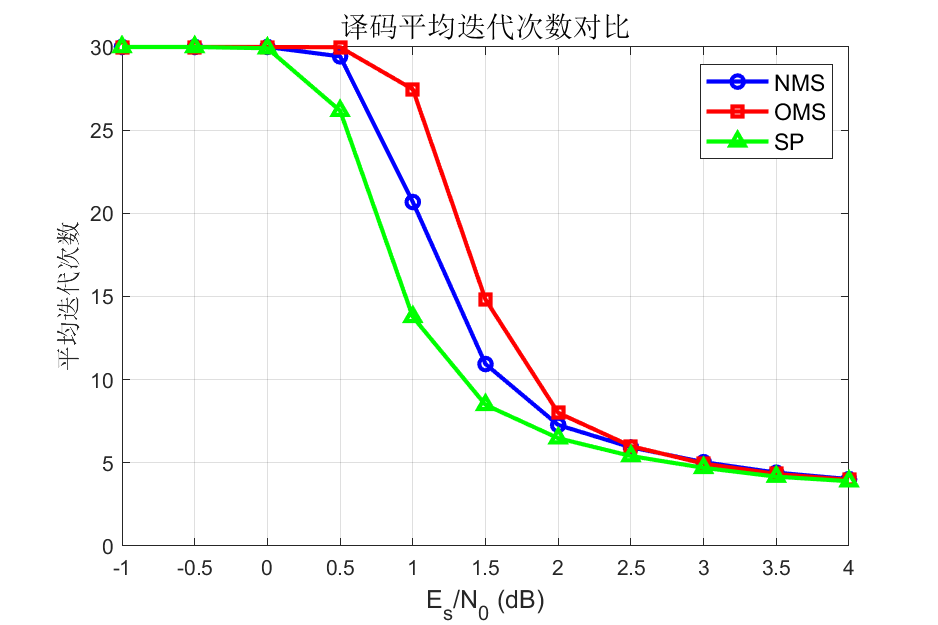
📊 性能实测 (R=1/2, A=1000, BPSK)

Eb/N0	NMS (α=0.75)	OMS (β=0.15)	SP (最优)	平均迭代
0.0 dB	2.05e-01	2.28e-01	1.56e-01	30
0.5 dB	1.54e-01	2.03e-01	8.04e-02	26~29
1.0 dB	3.41e-02	1.38e-01	7.07e-03	14~21
1.5 dB	6.45e-04	2.36e-02	6.40e-04	9~11
2.0 dB	0	7.40e-04	0	6~7

🎯 SP 算法理论最优，NMS 性能接近但复杂度低 60%！

💻 核心代码展示

🔥 双对角编码 (nrLDPCEncode.m)

% =========================================================================
% [TS 38.212 Section 5.3.2] 阶段1: 计算第一个核心奇偶节点
% =========================================================================
% 公式: p_0 = Σ_{j∈N(0)} π_{0,j}(c_j)
%       其中 π_{0,j} 表示循环移位操作
%
% 实现: 将前4层（双对角核心区域）的所有系统比特贡献累加
for iLayer = 1:4
    for iEdge = 1:nEdges
        % 获取连接的变量节点和移位量
        v_idx = edges(i_edge, 2);
        shift = shifts(i_edge);
        
        % [关键] 循环移位后异或累加
        p0_accum = xor(p0_accum, circshift(cwordMat(:, v_idx), -shift));
    end
end

🚀 层更新译码 + 早停机制 (nrLDPCDecode.m)

% =========================================================================
% 早停检测 (双重条件)
% =========================================================================
% 条件1: 硬判决稳定 (连续两次相同)
% 条件2: 前 4 层校验方程全通过 (H*c = 0)
​
if isequal(currHardDec, prevHardDec)
    % 检查部分校验和
    for iLayer = 1:4
        syndrome = zeros(Zc, 1);
        for iEdge = 1:nEdges
            % 循环移位后异或 (GF(2) 累加)
            syndrome = xor(syndrome, circshift(currHardDec(:, v_idx), -shift));
        end
        if any(syndrome), syndrome_pass = false; break; end
    end
    if syndrome_pass, break; end  % 校验通过，提前退出
end

🎬 一键运行

>> cd matlab
​
% 完整链路演示 (3GPP 流程详解)
>> demo_ldpc_e2e
​
% NMS/OMS/SP 算法性能对比
>> sim_algorithm_comparison
​
% 不同码率 (1/3, 1/2, 2/3, 3/4) BER 曲线
>> sim_code_rate_comparison

输出预览

╔══════════════════════════════════════════════════════════════════╗
║        5G NR LDPC 完整链路演示 (3GPP TS 38.212)                  ║
╚══════════════════════════════════════════════════════════════════╝

═══════════════════════════════════════════════════════════════════
【第一部分】 系统参数配置
═══════════════════════════════════════════════════════════════════

传输块参数:
  ├─ 信息比特长度 A = 1000 bits
  ├─ 目标码率 R = 0.500
  └─ 速率匹配输出长度 E = 2000 bits

[TS 38.212 Section 6.2.2] 基础图选择:
  ├─ 选择 Base Graph 2 (BG2)
  ├─ 原因: A <= 3824 且 R <= 0.67
  ├─ 系统比特长度 K = 1040 (= 10 × Zc)
  ├─ 完整码字长度 N = 5408 (= 52 × Zc)
  ├─ 提升因子 Zc = 104 (集合索引 i_LS = 7)
  └─ 填充比特数 n_F = K - A = 40 bits

═══════════════════════════════════════════════════════════════════
【第二部分】 发送端处理 (Transmitter)
═══════════════════════════════════════════════════════════════════

步骤 2.1: 生成随机传输块
  └─ 生成 1000 个随机信息比特

步骤 2.2: [TS 38.212 Section 5.2.2] 码块构造
  ├─ 信息比特长度 A = 1000
  ├─ 填充比特数 n_F = 40 (需要凑齐 K = 1040)
  │
  │  [公式] K' = 22 × Zc (BG1) 或 10 × Zc (BG2)
  │  [公式] n_F = K' - A (若 A < K')
  │
  └─ 构造消息向量: msg = [info_bits(1000) | filler_bits(40)] = 1040 bits

步骤 2.3: [TS 38.212 Section 5.3.2] LDPC 编码
  │
  │  【双对角编码原理】
  │  ├─ BG 矩阵的前4列对应核心奇偶节点
  │  ├─ 核心奇偶节点采用双对角结构 (易于求解)
  │  └─ 扩展奇偶节点直接由系统比特和核心奇偶计算
  │
  │  阶段1: p_0 = Σ(前4层所有系统比特贡献)
  │  阶段2: p_{1,2,3} = 递推计算
  │  阶段3: p_ext = f(系统比特, 核心奇偶)
  │
  ├─ 系统比特: 1040 bits (位置 1:1040)
  ├─ 奇偶比特: 4368 bits (位置 1041:5408)
  └─ 完整码字: 5408 bits

步骤 2.4: [TS 38.212 Section 5.4.2] 速率匹配
  │
  │  【速率匹配三步骤】
  │  (1) 缩短: 移除 n_F = 40 个填充比特
  │      └─ 位置: K - n_F + 1 到 K (即 1001 到 1040)
  │  (2) 打孔: 移除前 2×Zc = 208 个比特
  │      └─ 这些比特对应系统信息的前两个循环块
  │  (3) 循环缓冲: 输出 E = 2000 个比特
  │
  ├─ 缩短后长度: 5368 bits
  ├─ 打孔后长度 (循环缓冲): 5160 bits
  └─ 速率匹配输出: 2000 bits (重复因子 = 0.39)

步骤 2.5: BPSK 调制
  │  映射规则: 0 → +1, 1 → -1
  └─ 输出 2000 个 BPSK 符号

═══════════════════════════════════════════════════════════════════
【第三部分】 信道传输 (AWGN Channel)
═══════════════════════════════════════════════════════════════════

信道参数:
  ├─ Eb/N0 = 2.0 dB
  ├─ 实际码率 R = A/E = 0.5000
  ├─ Es/N0 = Eb/N0 + 10×log10(R) = -1.01 dB
  └─ 噪声标准差 σ = 0.7943

传输完成:
  └─ 接收 2000 个符号

═══════════════════════════════════════════════════════════════════
【第四部分】 接收端处理 (Receiver)
═══════════════════════════════════════════════════════════════════

步骤 4.1: LLR 计算
  │  公式: L(b) = 2y / σ² (BPSK + AWGN)
  ├─ 计算 2000 个信道 LLR 值
  └─ LLR 范围: [-10.66, 11.28]

步骤 4.2: [速率匹配逆操作] 速率恢复
  │
  │  【速率恢复操作】
  │  (1) LLR 累加: 重复传输位置的 LLR 相加
  │  (2) 打孔恢复: 前 2×Zc = 208 位置设为 LLR = 0
  │  (3) 填充恢复: 位置 1001 到 1040 设为 LLR = +∞
  │
  └─ 恢复后 LLR 长度: 5408 (= N)

步骤 4.3: LDPC 层更新译码
  │
  │  【层更新调度】
  │  for iLayer = 1:n_layers
  │      (1) VN→CN: 计算外信息 = LLR - 上次CN消息
  │      (2) CN更新: 使用 NMS/OMS/SP 算法
  │      (3) CN→VN: 反向移位并更新 LLR
  │  end
  │
  ├─ 算法: NMS (α = 0.75)
  ├─ 最大迭代次数: 30
  ├─ 实际迭代次数: 6 (早停生效: 是)
  └─ 输出 1000 个信息比特

═══════════════════════════════════════════════════════════════════
【第五部分】 性能评估
═══════════════════════════════════════════════════════════════════

传输结果:
  ├─ 发送比特数: 1000
  ├─ 错误比特数: 0
  ├─ 比特误码率 (BER): 0.00e+00
  └─ 帧误码 (FER): 0

  ✓ 传输成功，无误码!

═══════════════════════════════════════════════════════════════════
【第六部分】 3GPP TS 38.212 流程总结
═══════════════════════════════════════════════════════════════════

发送端流程:
  ┌──────────────────────────────────────────────────────────────┐
  │ 传输块 (A bits)                                              │
  │     ↓ [Section 5.1] CRC-24A/16 附加                          │
  │ B = A + L_crc                                                 │
  │     ↓ [Section 5.2.2] 码块分割 + CRC-24B                     │
  │ C 个码块，每个 K' bits                                       │
  │     ↓ [Section 5.2.2] Filler bits 插入                       │
  │ K = K' + n_F bits                                            │
  │     ↓ [Section 5.3.2] LDPC 编码                              │
  │ N = K + 奇偶比特 bits                                         │
  │     ↓ [Section 5.4.2] 速率匹配 (缩短+打孔+循环缓冲)          │
  │ E bits 输出                                                   │
  └──────────────────────────────────────────────────────────────┘

接收端流程:
  ┌──────────────────────────────────────────────────────────────┐
  │ E 个 LLR 值                                                   │
  │     ↓ 速率恢复 (逆速率匹配)                                  │
  │ N 个 LLR 值                                                   │
  │     ↓ LDPC 层更新译码                                        │
  │ K' 个信息比特                                                │
  │     ↓ 码块合并 + CRC 校验                                    │
  │ A 个信息比特                                                  │
  └──────────────────────────────────────────────────────────────┘

╔══════════════════════════════════════════════════════════════════╗
║                         演示完成!                               ║
╚══════════════════════════════════════════════════════════════════╝

• 🖥️ 运行环境

• MATLAB 版本: R2020a 或更高版本
• 依赖工具箱: 无 (纯 MATLAB 实现)

🛒 获取方式

关注公众号 【3GPP 仿真实验室】，后台回复关键词 【LDPC】 即可获取完整工程。

📚 参考文献

[1] 3GPP TS 38.212, "NR; Multiplexing and channel coding," v17.4.0, Dec. 2022.

[2] T. J. Richardson and R. L. Urbanke, "Efficient encoding of low-density parity-check codes," IEEE Trans. Inf. Theory, vol. 47, no. 2, pp. 638–656, Feb. 2001.

[3] J. Chen and M. P. C. Fossorier, "Near optimum universal belief propagation based decoding of low-density parity check codes," IEEE Trans. Commun., vol. 50, no. 3, pp. 406–414, Mar. 2002.

[4] E. Sharon, S. Litsyn, and J. Goldberger, "An efficient message-passing schedule for LDPC decoding," in Proc. IEEE ISTC, Sep. 2004, pp. 223–228.

[5] M. P. C. Fossorier, M. Mihaljević, and H. Imai, "Reduced complexity iterative decoding of low-density parity check codes based on beli