
教程全知识点简介:1.深度学习课程概述包括深度学习与机器学习区别、深度学习应用场景、深度学习框架介绍、项目演示、开发环境搭建(pycharm安装)。2. TensorFlow基础涵盖TF数据流图、TensorFlow实现加法运算、图与TensorBoard(图结构、图相关操作、默认图、创建图、OP)、张量(张量概念、张量的阶、张量数学运算)、变量OP(创建变量)、增加其他功能(命名空间、模型保存与加载、命令行参数使用)、逻辑回归案例。3. 神经网络基础包括playground使用、多个神经元效果演示、深层神经网络。4. 神经网络与tf.keras。5. 梯度下降算法改进涵盖指数加权平均、动量梯度下降法、RMSProp算法、Adam算法、TensorFlow Adam算法API、学习率衰减、标准化输入、神经网络调优、批标准化。6. 卷积神经网络包括CNN原理、CIFAR类别分类(API使用、步骤分析代码实现缩减版LeNet)、卷积神经网络学习特征可视化。7. 经典分类网络结构涵盖LeNet解析、AlexNet、卷积网络结构优化、Inception结构、pre_trained模型VGG预测(VGG模型使用、步骤代码)。8. CNN网络实战技巧。9. 迁移学习案例包括基于VGG的五种图片类别识别迁移学习(数据集迁移需求、思路步骤、训练时读取本地图片类别、特征图平均值输出替代全连接层)。10. 目标检测包括目标检测任务描述、目标定位实现思路、商品物体检测项目介绍、R-CNN(Overfeat模型、SPPNet)、Faster R-CNN(RPN原理)、YOLO(单元格grid cell、非最大抑制NMS、训练)、SSD。11. 商品检测数据集训练涵盖标注数据读取存储(xml读取本地文件存储pkl、解析结构、one_hot编码函数)、训练(案例训练结果、多GPU训练代码修改)、本地预测测试(预测代码)、模型导出(keras模型TensorFlow导出)。12. 模型部署包括Web与模型服务对接逻辑、Docker部署环境、TF Serving与Web开启服务(安装Tensorflow Serving、commodity模型服务运行)、TensorFlow Client对接模型服务、Web Server开启。

神经网络与tf.keras
1.4 深层神经网络
学习目标
-
目标
- 了解深层网络的前向传播与反向传播的过程
-
应用
-
无
-
为什么使用深层网络
对于人脸识别等应用,神经网络的第一层从原始图片中提取人脸的轮廓和边缘,每个神经元学习到不同边缘的信息;网络的第二层将第一层学得的边缘信息组合起来,形成人脸的一些局部的特征,例如眼睛、嘴巴等;后面的几层逐步将上一层的特征组合起来,形成人脸的模样。随着神经网络层数的增加,特征也从原来的边缘逐步扩展为人脸的整体,由整体到局部,由简单到复杂。层数越多,那么模型学习的效果也就越精确。
通过例子可以看到,随着神经网络的深度加深,模型能学习到更加复杂的问题,功能也更加强大。
1.4.1 深层神经网络表示
1.4.1.1 什么是深层网络?
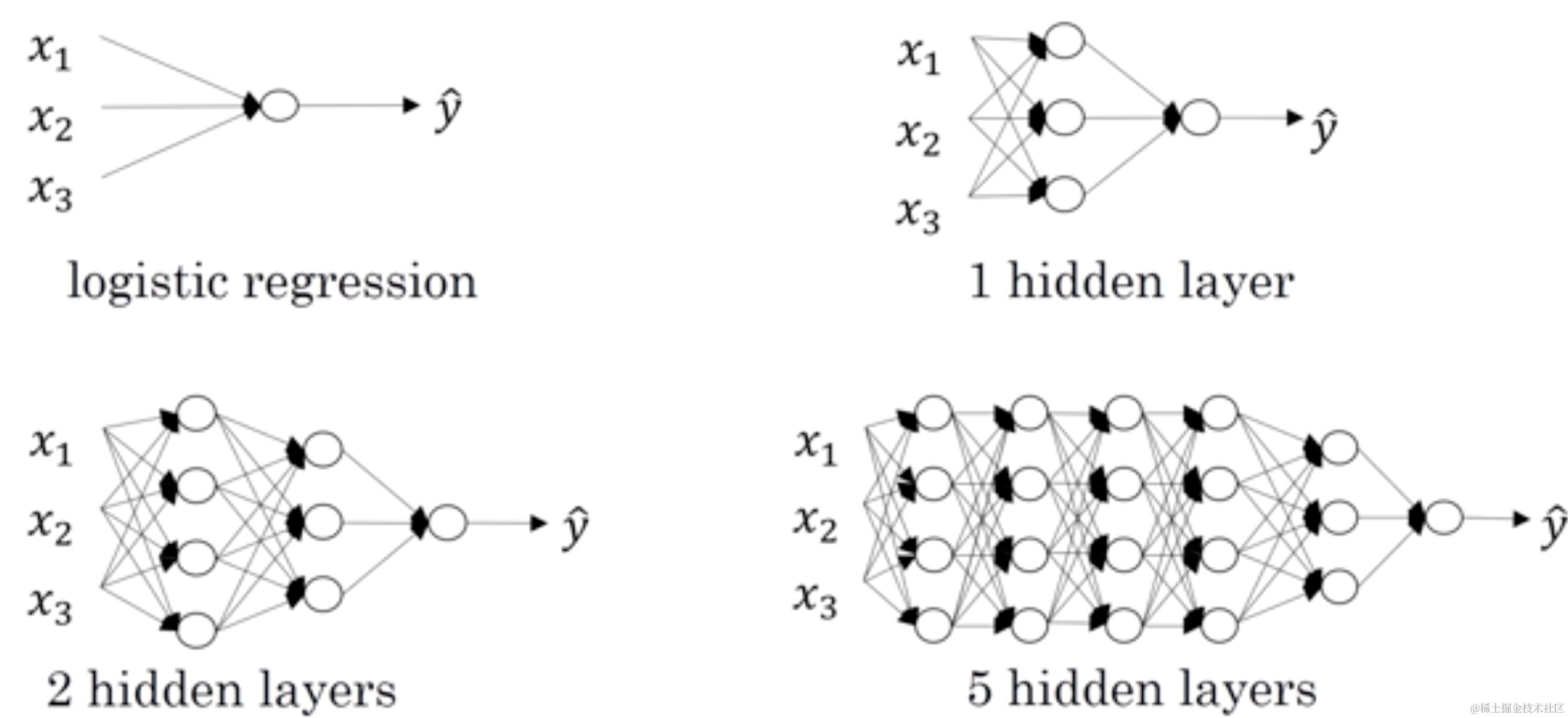
使用浅层网络的时候很多分类等问题得不到很好的解决,所以需要深层的网络。
1.4.2 四层网络的前向传播与反向传播

在这里首先对每层的符号进行一个确定,我们设置L为第几层,n为每一层的个数,L=[L1,L2,L3,L4],n=[5,5,3,1]
1.4.2.1 前向传播
首先还是以单个样本来进行表示,每层经过线性计算和激活函数两步计算
z[1]=W[1]x+b[1],a[1]=g1z^{[1]} = W^{[1]}x+b^{[1]}, a^{[1]}=g^{[1]}(z^{[1]})z[1]=W[1]x+b[1],a[1]=g[1](z[1])xxxa[1]a^{[1]}a[1]
z[2]=W[2]a[1]+b[2],a[2]=g2z^{[2]} = W^{[2]}a^{[1]}+b^{[2]}, a^{[2]}=g^{[2]}(z^{[2]})z[2]=W[2]a[1]+b[2],a[2]=g[2](z[2])a[1]a^{[1]}a[1]a[2]a^{[2]}a[2]
z[3]=W[3]a[2]+b[3],a[3]=g3z^{[3]} = W^{[3]}a^{[2]}+b^{[3]},a^{[3]}=g^{[3]}(z^{[3]})z[3]=W[3]a[2]+b[3],a[3]=g[3](z[3])a[2]a^{[2]}a[2]a[3]a^{[3]}a[3]
z[4]=W[4]a[3]+b[4],a[4]=σ(z[4])z^{[4]} = W^{[4]}a^{[3]}+b^{[4]},a^{[4]}=\sigma(z^{[4]})z[4]=W[4]a[3]+b[4],a[4]=σ(z[4])a[3]a^{[3]}a[3]a[4]a^{[4]}a[4]
我们将上式简单的用通用公式表达出来,x=a[0]x = a^{[0]}x=a[0]
z[L]=W[L]a[L−1]+b[L],a[L]=gLz^{[L]} = W^{[L]}a^{[L-1]}+b^{[L]}, a^{[L]}=g^{[L]}(z^{[L]})z[L]=W[L]a[L−1]+b[L],a[L]=g[L](z[L])a[L−1]a^{[L-1]}a[L−1]a[L]a^{[L]}a[L]
- m个样本的向量表示
Z[L]=W[L]A[L−1]+b[L]Z^{[L]} = W^{[L]}A^{[L-1]}+b^{[L]}Z[L]=W[L]A[L−1]+b[L]
A[L]=gLA^{[L]}=g^{[L]}(Z^{[L]})A[L]=g[L](Z[L])
输入a[L−1]a^{[L-1]}a[L−1]a[L]a^{[L]}a[L]
1.4.2.2 反向传播
因为涉及到的层数较多,所以我们通过一个图来表示反向的过程

- 反向传播的结果(理解)
单个样本的反向传播:
dZ[l]=dJda[l]da[l]dZ[l]=da[l]∗g[l]′(Z[l])dZ^{[l]}=\frac{dJ}{da^{[l]}}\frac{da^{[l]}}{dZ^{[l]}}=da^{[l]}*g^{[l]}{'}(Z^{[l]})dZ[l]=da[l]dJdZ[l]da[l]=da[l]∗g[l]′(Z[l])
dW[l]=dJdZ[l]dZ[l]dW[l]=dZ[l]⋅a[l−1]dW^{[l]}=\frac{dJ}{dZ^{[l]}}\frac{dZ^{[l]}}{dW^{[l]}}=dZ^{[l]}\cdot a^{[l-1]}dW[l]=dZ[l]dJdW[l]dZ[l]=dZ[l]⋅a[l−1]
db[l]=dJdZ[l]dZ[l]db[l]=dZ[l]db^{[l]}=\frac{dJ}{dZ^{[l]}}\frac{dZ^{[l]}}{db^{[l]}}=dZ^{[l]}db[l]=dZ[l]dJdb[l]dZ[l]=dZ[l]
da[l−1]=W[l]T⋅dZ[l]da^{[l-1]}=W^{[l]T}\cdot dZ^{[l]}da[l−1]=W[l]T⋅dZ[l]
多个样本的反向传播
dZ[l]=dA[l]∗g[l]′(Z[l])dZ^{[l]}=dA^{[l]}*g^{[l]}{'}(Z^{[l]})dZ[l]=dA[l]∗g[l]′(Z[l])
dW[l]=1mdZ[l]⋅A[l−1]TdW^{[l]}=\frac{1}{m}dZ^{[l]}\cdot {A^{[l-1]}}^{T}dW[l]=m1dZ[l]⋅A[l−1]T
db[l]=1mnp.sum(dZ[l],axis=1)db^{[l]}=\frac{1}{m}np.sum(dZ^{[l]},axis=1)db[l]=m1np.sum(dZ[l],axis=1)
dA[l]=W[l+1]T⋅dZ[l+1]dA^{[l]}=W^{[l+1]T}\cdot dZ^{[l+1]}dA[l]=W[l+1]T⋅dZ[l+1]
1.4.3 参数与超参数
1.4.3.1 参数
参数即是我们在过程中想要模型学习到的信息(模型自己能计算出来的),例如 W[l]W[l],b[l]b[l]。而**超参数(hyper parameters)**即为控制参数的输出值的一些网络信息(需要人经验判断)。超参数的改变会导致最终得到的参数 W[l],b[l] 的改变。
1.4.3.2 超参数
典型的超参数有:
- 学习速率:α
- 迭代次数:N
- 隐藏层的层数:L
- 每一层的神经元个数:n[1],n[2],...
- 激活函数 g(z) 的选择
当开发新应用时,预先很难准确知道超参数的最优值应该是什么。因此,通常需要尝试很多不同的值。应用深度学习领域是一个很大程度基于经验的过程。
1.4.3.3 参数初始化
- 为什么要随机初始化权重
如果在初始时将两个隐藏神经元的参数设置为相同的大小,那么两个隐藏神经元对输出单元的影响也是相同的,通过反向梯度下降去进行计算的时候,会得到同样的梯度大小,所以在经过多次迭代后,两个隐藏层单位仍然是对称的。无论设置多少个隐藏单元,其最终的影响都是相同的,那么多个隐藏神经元就没有了意义。
在