自用华为ICT云赛道AI第五章知识点-量子计算简介,量子计算基本理论
量子计算简介
量子是什么?从连续到离散的认知

- 1.1物理量被视作是连续的,系统的能量可以取得任意值,比如初始时小球可以从任意位置释放,因此系统能量的可能取值是一条光滑连续的抛物线。
- 1.2物理量是量子化的,系统的能量只能取分立的值,比如量子谐振子的能量只能取hw/2、3hw/2等值,并且能量之间的差值必定是hw的整数倍。在这里,hw就是一个能量量子。
- 2.1系统的运动状态可以完全确定和预测的。对于经典谐振子,其动能(速度)和势能(位置)可以同时为0,比如初始时小球位于弹簧的平衡位置,系统能量为0。
- 2.2量子力学的不确定性原理表明我们无法同时确定一个系统的精确位置和动量。对于量子谐振子,其动能(速度)和势能(位置)无法同时为0,因此系统能量存在最小值hw/2。
- 3.1经典物理学认为大多数的物质由粒子构成。
- 3.2量子力学则表明粒子既具有波动性(波函数叠加),又具有粒子性(波函数坍缩)。
量子力学基本概念

量子计算发展

- 1992年Deutsch-Jozsa算法属于最早一批量子算法的例子,它证明了量子算法相对于经典算法有指数级别的加速能力
- 1998年:BernhardOmer提出量子计算编程语言
- 2016年,IBM发布了6量子比特的可编程的量子计算机。
- 2009年,MIT三位科学家联合开发了一种求解线性系统的量子算法。
- 讲解词来自:波士顿咨询量子计算报告:2030年市场规模将达500亿美元
- 1、显著的速度优势:经典计算机是按顺序运行的,这对于大型、复杂的问题就很困难,比如大数因数分解(破解最常见的密码体系)。相比之下,量子计算机相当于提供了一个天然的并行运算,能够同时试验多个可能的解,比已知最快经典算法有“指数型(超多项式)”加速。
- 2、温和的速度优势:面向非结构化的搜索任务,包括一些机器学习的应用,运算时间也会随着问题规模指数性增长。此时,量子算法,如Grover搜索的优势就体现出来了。Grover搜索利用量子态的纠缠特性和量子并行计算原理,运算时间仅随着问题规模线性增长。
- 3、不明确的速度优势:当前的经典量子计算在解决路由运输和物流优化等复杂操作或网络的问题是,已经显现了良好的性能
量子计算应用场景和优势

量子计算基本理论
量子比特和量子态

- 带大家看看量子计算到底是怎么回事,是怎么计算的。对于经典比特我们已经非常熟悉了,它就是利用电位的高低来表示二进制的零一,进而有了我们现在的计算机体系。但是在这里有一个问题,N个经典比特在同一时间只能表示一个数。接下来我们看看量子比特是怎么解决这个问题的。那么什么是量子比特呢?在实验上比较常用的有超导量子比特、离子阱量子比特和NV色性量子比特。每个系统都有每个系统的特性。这我们以自旋为例来分析一下。我们知道,经典比特的状态要么是零要么是一,但量子世界很奇特,粒子的自旋可以同时处于向上或者向下,就像这枚旋转的硬币,它可以同时处于文字那一面和国徽那一面,不对他进行观察,他就不是确定的,这就是量子叠加原理。另外我们还有量子纠缠原理,当两个硬币发生纠缠后,如果我们对其中一个硬币进行观察得到国徽,那另一枚硬币也会立马坍缩到国徽那一面,而且跟距离无关。

量子门

- 有了比特过后,需要的就是对比特进行操控的逻辑门了,就像经典比特有与非门等逻辑门可以对比特进行操控,量子比特也有对应的量子逻辑门,例如这里有X门,Y门、Z门等等。它产生的效果可以用一些矩阵来表示,举个例子,X门可以完成比特翻转的任务,它可以将0态翻转为1态,1态翻转为0态。另外一类量子门是旋转门,他可以将量子比特绕着希尔伯特空间中的不同轴来进行旋转,这些旋转角度是可以任意设置的,这也是后面我们搭建可训练的神经网络的基础。当然还有一些量子逻辑门相对较复杂,这里就不展开来讲了。
- 么正变换(Unitary transformation)
基础量子门作用及表示


量子线路
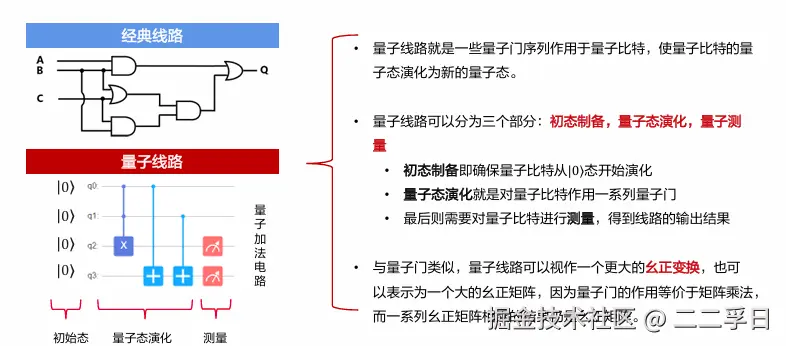
- 有了逻辑门过后,接下来的就是怎么组织这些逻辑门,来让他完成指定的任务。左边是我们非常熟悉的电子线路,它会对电位进行相应的处理,完成逻辑运算,而且人们也证明了,只要几个基本的逻辑门就能完成所有的逻辑操作。在量子层面上,我们也可以将量子逻辑门组织起来,对量子比特进行操作,完成我们的算法,例如右边这幅图,左边的两个零表示的是两个初始状态处在零态的量子比特,然后我们在第一个比特上作用一个哈达马达门,再作用一个控制非门,这个线路就能够来制备一个前面提到的纠缠态的线路。
- 有了逻辑门过后,接下来的就是怎么组织这些逻辑门,来让他完成指定的任务。左边是我们非常熟悉的电子线路,它会对电位进行相应的处理,完成逻辑运算,而且人们也证明了,只要几个基本的逻辑门就能完成所有的逻辑操作。在量子层面上,我们也可以将量子逻辑门组织起来,对量子比特进行操作,完成我们的算法,例如右边这幅图,左边的两个零表示的是两个初始状态处在零态的量子比特,然后我们在第一个比特作用一个哈达马达门,再作用一个控制非门,这个线路就能够来制备一个前面提到的纠缠态的线路。
制备贝尔态的量子线路

基础量子算法一Deutsch算法

通用量子算法应用场景和优势
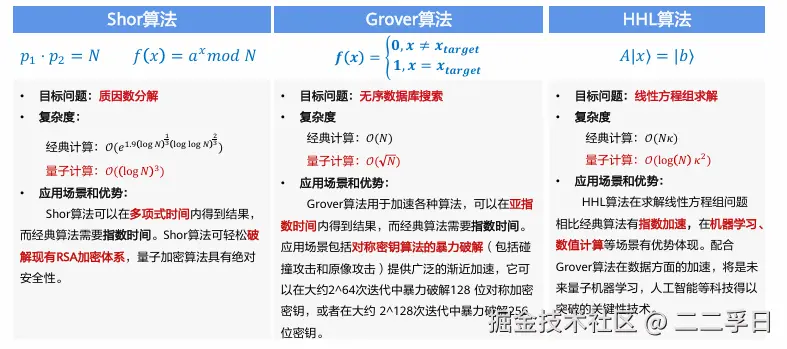
- Grover算法应用场景包括对称密钥算法的暴力破解(包括碰撞攻击和原像攻击)提供广泛的渐近加速,它可以在大约2^64次迭代中暴力破解128位对称加密密钥,或者在大约2^128次迭代中暴力破解256位密钥。
变分量子算法介绍

- VQA的输入是:对问题的解进行编码的损失函数C(θ),对参数进行训练以最小化损失的ansatz,以及(可能)在优化过程中使用的一组训练数据。在循环的每一次迭代中,我们都会使用量子计算机来有效地估计损失(或其梯度)。这些信息被输入到一台经典的计算机中,该计算机利用优化器的能力来解优化问题。一旦满足终止条件,VQA将输出问题解决方案的估计值。输出的形式取决于具体问题。图中显示了一些最常见的输出类型。
变分量子算法应用场景

VQE量子化学

- 量子化学(quantumchemistry)是理论化学的一个分支学科,是应用量子力学的基本原理和方法研究化学问题的一门基础科学。研究范围包括稳定和不稳定分子的结构、性能及其结构与性能之间的关系;分子与分子之间的相互作用;分子与分子之间的相互碰撞和相互反应等问题。
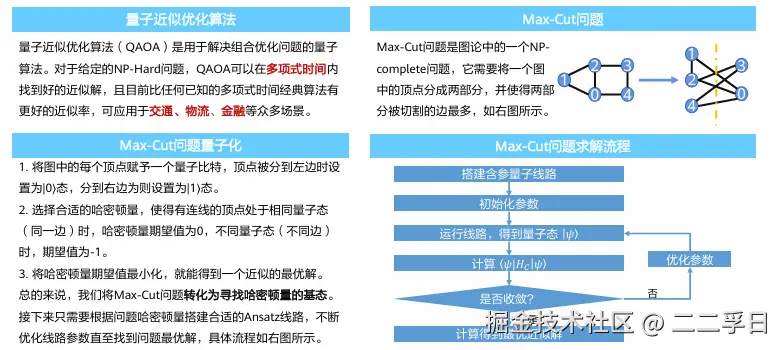
QAOA量子近似优化算法
