【本章主要内容】
- 数组的概念和初始化
- 数组的常见算法及应用
- 数组工具类的使用及常见异常
一、概述
1、什么是数组
在Java中,数组 (Array) 是一个用于存储固定数量、相同类型元素的容器。通过一个统一的数组名来引用这组数据,并通过从0开始的索引 (Index) 来访问其中的每一个元素 (Element) 。
- 数组名: 通过一个变量名对一组数据进行统一命名,这个变量名被称为数组名
- 下标或索引:通过编号的方式对这些数据进行使用和管理,这个编号被称为下标或索引(从 0 开始)。
- 元素:数组中的每一个数据称为元素(Element)。
- 长度:数组中元素的总个数被称为数组的长度(Length)。
2、分类

- 基本数据类型数组是指数组元素是 8 种基本数据类型的值
- 引用数据类型数组是指数组元素中存储的是对象,也称为对象数组
3、特点
- 类型统一:一个数组中所有元素的数据类型必须完全相同。
- 长度固定:数组一旦被创建,其长度 (Length) 就不可改变。
- 内存连续:数组在内存中会开辟一整块连续的空间,数组中的元素在内存中是依次紧密排列的,有序的。这使得通过索引访问元素的速度非常快。
- 引用类型:数组名本身是一个引用变量,它指向堆内存中数组对象的首地址。
二、一维数组
1、声明
数据类型[] 数组名; // 首选的方法
或
数据类型 数组名[]; // 效果相同,但不是首选方法,来自 C/C++ 语言 ,在Java中采用是为了让 C/C++ 程序员能够快速理解java语言。
【注意】: 数组声明的明确事项
- 数组的维度:在 Java 中数组的符号是[],[]表示一维,[] []表示二维。
- 数组的元素类型:dataType,即创建的数组容器可以存储什么数据类型的数据。元素的类型可以是任意的 Java 的数据类型。例如:int、String、Student 等。
- 数组名:arrayRefVar 就是代表某个数组的标识符,数组名其实也是变量名,按照变量的命名规范来命名。数组名是个引用数据类型的变量,因为它代表一组数据。
2、初始化
所谓的初始化是指确定数组的长度和元素的值。因为只有确定了数组的长度,才能为数组开辟对应大小的内存空间。数组的初始化可以分为静态初始化和动态初始化。
(1)静态初始化
静态初始化:在声明时就直接指定数组中包含的元素,由编译器自动计算数组长度。
静态初始化有两种格式,下面分别对两种格式进行说明(合并了声明和初始化)。
// 格式一,完整格式
数据类型[] 数组名 = new 数据类型[]{元素1,元素2...,元素k};
//格式二,常用,Java的类型推断机制,简化了代码的书写。
数据类型[] 数组名 = {元素1,元素2...,元素k};
// 注意:简化格式必须在一条语句中完成声明和初始化,以下写法是错误的!
// int[] arr3;
// arr3 = {10, 20, 30, 40}; // 编译错误
【注意】
- 在以上两种语法格式中,要求大括号中的各元素用逗号隔开。
- 元素可以重复,元素个数也可以是零个或多个。
- 格式 2 是格式 1 的简化,二者没有本质的区别。
- 格式 2 不能像格式 1 先声明再进行初始化,必须在一个语句中完成,如下所示的代码就会报错:
(2)动态初始化
动态初始化:在声明时只指定数组的长度,这也是动态初始化与静态初始化的主要区别。数组中每个元素的值由系统根据其类型赋予默认值。
动态初始化的语法格式如下所示(合并了声明和初始化)。
数据类型[] 数组名 = new 数据类型[数组长度];
// 例如:动态初始化一个长度为5的int数组
int[] arr = new int[5];
【注意】
- 数组长度:表示数组可以容纳的元素数量。必须是一个整数表达式,它可以是一个整数常量、一个整数变量,或者是任何返回整数值的表达式。
- 数组有定长特性,长度一旦指定,不可更改。
- 数组的索引将从
0 开始,到数组长度 - 1 结束。
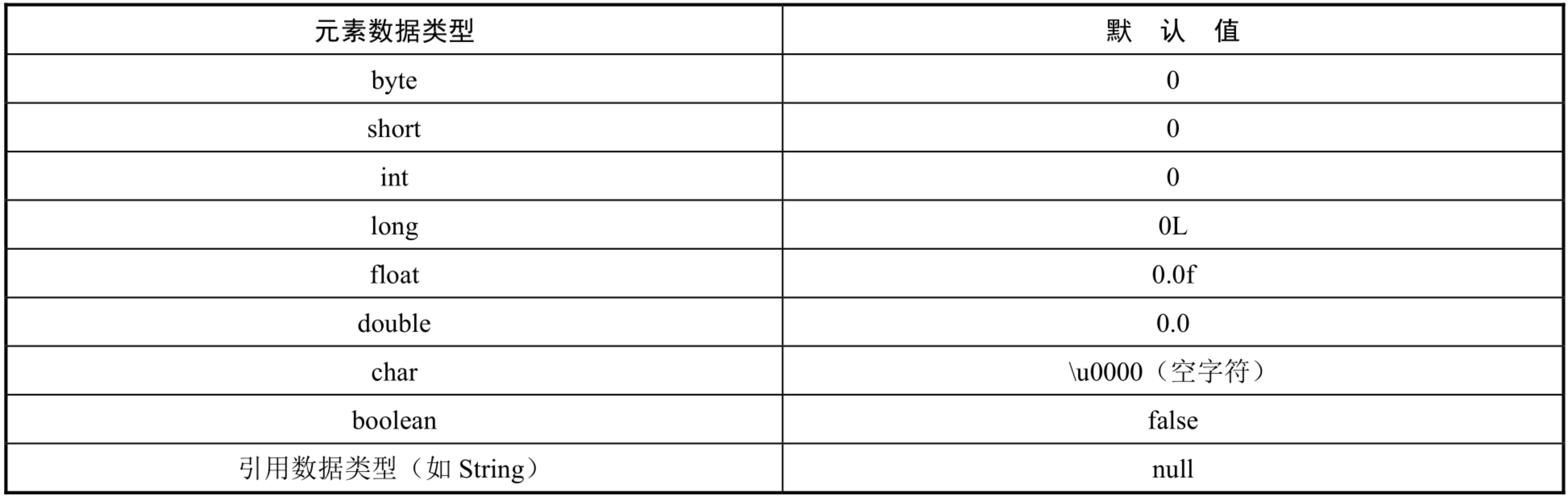
【元素的默认值】
动态初始化后,由于没有指定数组元素,数组元素会自动获得默认值。
3、访问与遍历
(1)元素访问

public class Array {
public static void main(String[] args) {
// 创建数组
int[] arr = {1, 2, 3, 4, 5};
// 输出数组长度和第一个元素
System.out.println(arr.length);
System.out.println(arr[0]);
// 修改第一个元素
arr[0] = 10;
// 输出修改后的第一个元素
System.out.println(arr[0]);
// 获取数组的最后一个元素
System.out.println(arr[arr.length - 1]);
// 尝试访问超出数组长度的元素
System.out.println(arr[arr.length]); // 报错:索引越界异常:java.lang.ArrayIndexOutOfBoundsException: 5
}
}
(2)数组遍历
数组遍历就是对数组中的元素按顺序依次进行访问。
// 传统遍历
class ArrayElementl {
public static void main(String[] args) {
// 创建数组
int[] arr = {10, 20, 30};
// 遍历数组
System.out.println("数组的第一个元素是:" + arr[0]);
System.out.println("数组的第二个元素是:" + arr[1]);
System.out.println("数组的第三个元素是:" + arr[2]);
}
}
// for循环遍历
// 创建数组
int[] arr = {10, 20, 30};
for (int i = 0; i < arr.length; i++) {
System.out.println("数组的第" + (i + 1) + "个元素是:" + arr[i]);
}
// 增强 for 循环 (for-each)遍历
int[] arr = {1, 2, 3, 4, 5};
for (int element : arr) {
System.out.println("元素值为: " + element);
}
4、内存分析
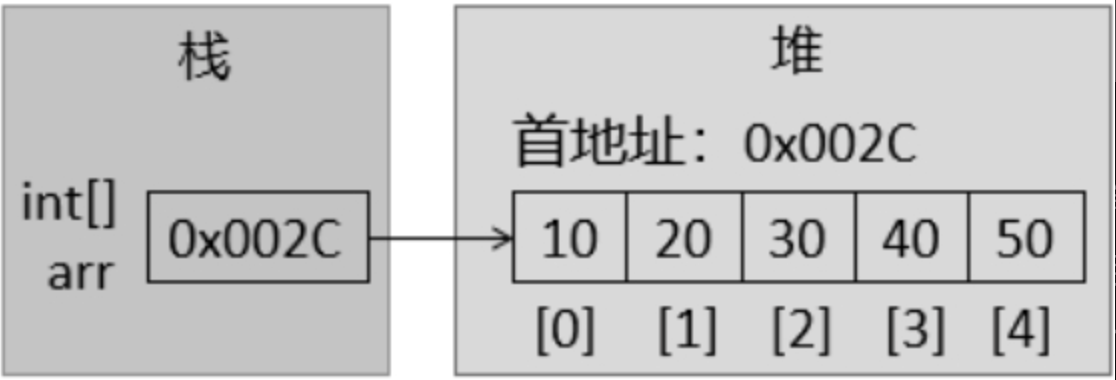
(1)连续的内存空间
当一个数组被初始化时,Java虚拟机(JVM)会在堆内存中为其分配一整块连续的存储空间。
- 空间大小:系统根据数组的元素类型确定每个存储单元的大小(例如,
int类型占4个字节),再根据数组长度决定开辟多少个这样的单元格,并将元素依次放在对应的空间中。 - 数组引用:我们使用的数组名(例如
arr)是一个引用变量,它存储的正是这块连续内存空间的首地址。
(2)寻址原理:首地址与偏移量
-
定位方式:知道了首地址,就可以通过索引(下标)计算出偏移量,从而快速定位到任何一个元素。
- 访问第一个元素
arr[0],就是访问首地址本身(偏移量为0)。 - 访问第二个元素
arr[1],就是在首地址的基础上偏移一个元素的存储宽度。
- 访问第一个元素
-
形象比喻:这个过程就像和朋友们住宾馆,房间都是挨着的。只要找到了第一个房间(首地址),根据房间号的顺序(索引),就能立刻找到其他任何一个房间。
虽然数组名变量中确实存储了地址信息,但Java出于安全和抽象的考虑,并不会直接向用户暴露真实的内存地址。
当我们尝试直接打印数组名(如 System.out.println(arr);),控制台显示的并不是内存地址值,而是一串代表对象信息的字符串。形如 [I@7a81197d,其含义是:
-
[ : 代表这是一个数组。 -
I : 代表数组的元素类型是int。 -
@ : 分隔符。 -
7a81197d : 这是对象的哈希码 (Hash Code) ,它由内存地址计算得来,可以看作是对象的唯一标识,但并非地址本身。
三、数组的赋值与复制
在Java中,变量的赋值行为取决于其数据类型。通过下面的代码,我们可以清晰地看到基本数据类型和引用数据类型(如数组)在赋值时的根本不同。
public class AssignmentTest {
public static void main(String[] args) {
// --- 基本数据类型:值拷贝 ---
int a = 1;
int b = a; // 将a的值复制一份给b
System.out.println("a = " + a + ", b = " + b); // a = 1, b = 1
b = 2; // 修改b的值
System.out.println("修改后, a = " + a + ", b = " + b); // a = 1, b = 2 (a未受影响)
// --- 引用数据类型(数组):引用地址值拷贝 ---
int[] arr1 = {2, 3, 5, 7, 11};
int[] arr2 = arr1; // 将arr1的引用地址值复制给arr2
System.out.println("arr1: " + java.util.Arrays.toString(arr1)); // arr1: [2, 3, 5, 7, 11]
System.out.println("arr2: " + java.util.Arrays.toString(arr2)); // arr2: [2, 3, 5, 7, 11]
arr2[0] = 0; // 通过arr2修改数组元素
System.out.println("修改后, arr1: " + java.util.Arrays.toString(arr1)); // arr1: [0, 3, 5, 7, 11] (arr1受到影响)
System.out.println("修改后, arr2: " + java.util.Arrays.toString(arr2)); // arr2: [0, 3, 5, 7, 11]
}
}
(注:为了更清晰地展示数组内容,代码中使用了 java.util.Arrays.toString() 方法。)
1、基本数据类型:值的复制
当执行 int b = a; 时,Java进行了值拷贝。
- 内存行为:系统会在栈内存中为变量
b 开辟一块新的、独立的空间,然后将变量a 中存储的具体数值 (1) 复制到b 的空间中。 - 结果:
a 和b 是两个完全独立的变量,各自持有自己的数据。因此,修改其中一个变量的值,对另一个变量毫无影响。
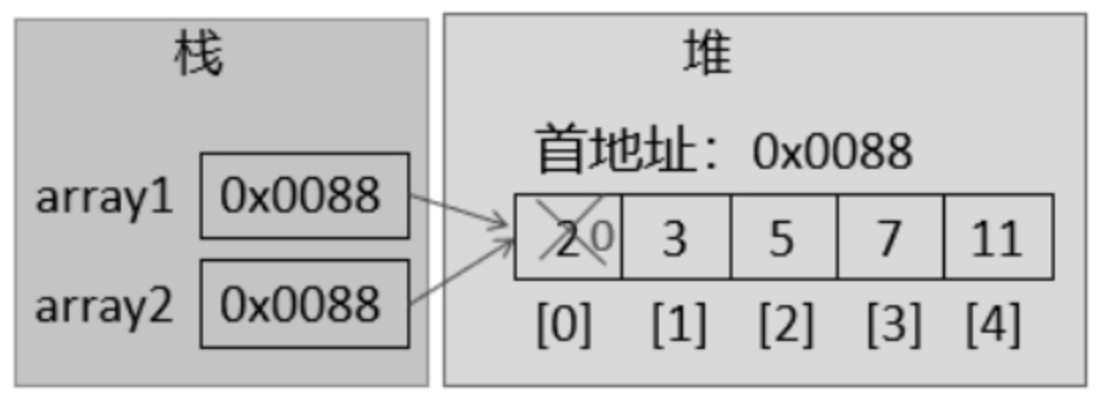
2、数组(引用类型):地址值的复制
当执行 int[] arr2 = arr1; 时,Java进行了引用拷贝。
- 内存行为:数组是引用类型,其实际数据(元素
1, 2, 3)存储在堆内存中。变量
arr1 本身在栈内存中并不存储这些数据,而是存储了该数组对象在堆中的内存地址。
这句赋值语句的本质是:将arr1 变量中所存储的地址值,复制一份给了arr2。 - 结果:
arr1 和arr2 这两个引用变量,现在指向了堆内存中同一个数组对象。它们就像是同一间房子的两把钥匙。无论用哪把钥匙开门进去修改了房间里的东西,另一把钥匙下次开门时看到的也必然是修改后的结果。
3、结论
- 对基本数据类型进行赋值操作,是值的复制。
- 对引用数据类型(包括数组、所有对象)进行赋值操作,是引用的复制(即地址的复制)。
四、数组算法
1、数组元素特征值
数组元素的特征值统计是非常基础的算法,常见的操作有统计数组中满足某特征元素的个数、求元素的最值、平均值、总和等。
(1)求总和、均值
// 求总和、均值
public class TestArraySum {
public static void main(String[] args) {
int[] arr = {4,5,6,1,9};
int sum = 0; // 因为0加上任何数都不影响结果
for(int i=0;i<arr.length;i++){
sum += arr[i];
}
System.out.println("总和为:" + sum);
double mean = (double)sum/arr.length;
System.out.println("均值为:" + mean);
}
}
(2)求总乘积
// 求总乘积
public class TestArrayMul {
public static void main(String[] args) {
int[] arr = {4,5,6,1,9};
long result = 1; // 因为1乘以任何数都不影响结果
for(int i=0; i<arr.length; i++){
result *= arr[i];
}
System.out.println("总乘积为: " + result);
}
}
2、数组元素反转
实现思想: 数组对称位置的元素互换。
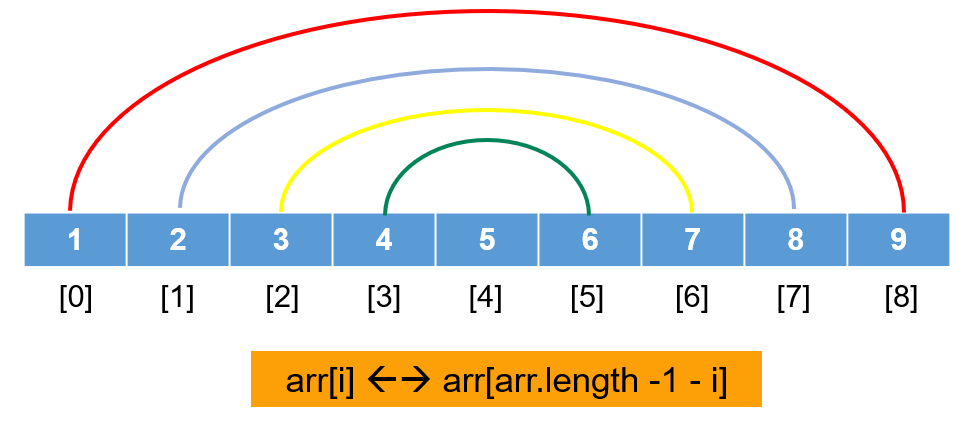
方法一:使用 for 循环原地反转数组
这是最直接的方法,通过交换数组两端的元素来实现反转。
-
确定交换几次
次数 = 数组.length / 2 -
谁和谁交换
for(int i=0; i< arr.length / 2; i++){ int temp = arr[i]; // 使用 temp 临时变量存储 arr1[i] 的值 arr[i] = arr[arr.length-1-i]; // 将数组末尾的元素 arr1[arr.length - 1 - i] 赋值给 arr1[i] arr[arr.length-1-i] = temp; // 将 temp 中存储的原始 arr1[i] 值赋值给 arr1[arr - 1 - i],完成交换。 }
【举例】
int[] arr1 = {1, 2, 3, 4, 5}; // 原数组
int n = arr1.length; // 获取数组长度
// 使用 for 循环反转的核心代码
for (int i = 0; i < n / 2; i++) {
int temp = arr1[i];
arr1[i] = arr1[n - 1 - i];
arr1[n - 1 - i] = temp;
}
// 打印反转后的数组
for (int i = 0; i < arr1.length; i++) {
System.out.print(arr1[i] + " ");
}
方法二:使用辅助数组
这种方法通过创建一个新的数组,并将原数组的元素从后向前复制到新数组中来实现反转。不过此时,相当于堆中有两个数组,在内存中占了 2 倍的空间。
【举例】
int[] arr1 = {1, 2, 3, 4, 5}; // 原数组
int[] arr2 = new int[arr1.length]; // 创建一个新的数组用于存储反转后的元素,其长度与 arr1 相同
for (int i = 0; i < arr1.length; i++) {
arr2[i] = arr1[arr1.length - 1 - i]; // 将原数组 arr1 的元素从后向前依次复制到新数组 arr2
}
// 打印反转后的新数组
for (int i = 0; i < arr2.length; i++) {
System.out.print(arr2[i] + " ");
}
4、数组元素排序算法
(1)排序的基本概念
1. 定义
排序,就是将一组记录(如数组中的元素)按照其关键字(通常是元素值本身)的某种顺序(如升序或降序)进行重新排列的过程。
2. 目的
排序的主要目的之一是为了后续的高效查找。例如,在有序数组中使用二分查找,其效率远高于在无序数组中的线性查找。
3. 分类
- 内部排序:所有排序操作都在内存中完成。适用于数据量不大,可以一次性载入内存的场景。我们通常接触的都是内部排序。
- 外部排序:当数据量巨大,无法一次性全部加载到内存时,需要借助磁盘等外部存储进行排序。外部排序通常是内部排序的延伸和组合。
(2)衡量算法的标尺
我们通过以下三个核心指标来评估一个排序算法的优劣:
1. 时间复杂度 (Time Complexity)
-
概念:它衡量的是算法的执行时间随数据规模
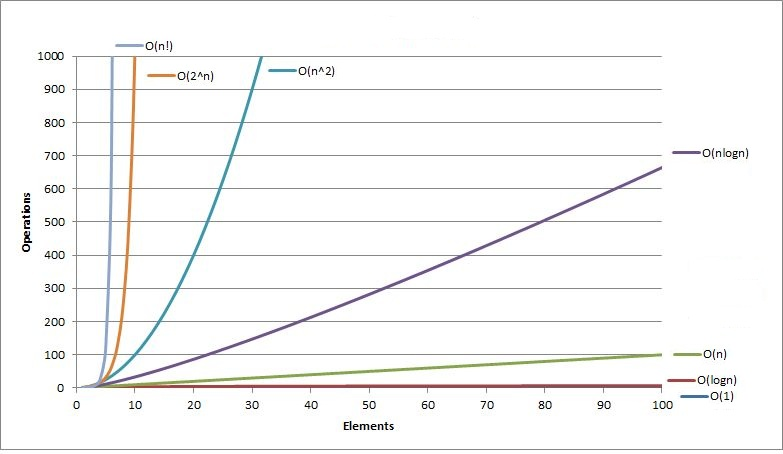
n 增长而变化的趋势,通常用大O表示法O(f(n)) 来表示。时间复杂度关心的是增长率,而不是精确的执行时间。 -
常见复杂度(从优到劣) : O(1) < O(log n) < O(n) < O(n log n) < O(n**2 ) < O(n3 ) < O(2n** )
(注:在算法领域,
log n 通常指以2为底的对数)
2. 空间复杂度 (Space Complexity)
- 概念:它衡量的是算法在运行过程中所需要消耗的额外存储空间。我们关注的是除了存储原始数据外,算法本身需要多少辅助内存。
3. 稳定性 (Stability)
- 概念:如果待排序的序列中有两个相等的元素,在排序后,它们原来的相对前后顺序保持不变,则称该排序算法是稳定的;反之,则为不稳定的。
(4)常见内部排序算法
| 排序算法 | 平均时间复杂度 | 最坏时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| 冒泡排序 | O(n2) | O(n2) | O(1) | 稳定 |
| 选择排序 | O(n2) | O(n2) | O(1) | 不稳定 |
| 插入排序 | O(n2) | O(n2) | O(1) | 稳定 |
| 快速排序 | O(n log n) | O(n2) | O(log n) | 不稳定 |
| 归并排序 | O(n log n) | O(n log n) | O(n) | 稳定 |
| 堆排序 | O(n log n) | O(n log n) | O(1) | 不稳定 |
如何选择?
-
若
n 非常小 (如 n ≤ 50) :- 可选用直接插入排序或直接选择排序。
- 如果数据基本有序,插入排序表现更佳。
-
若
n 较大:- 应采用时间复杂度为 O(n log n) 的排序方法,如快速排序、堆排序或归并排序。
- 快速排序:平均性能最佳,是实际应用中最常用的排序算法之一。
- 归并排序:性能稳定,时间复杂度始终为 O(n log n),且是稳定排序,常用于需要稳定性的场景。
- 堆排序:性能同样稳定,且空间复杂度优于归并排序。
(5)冒泡排序(BubbleSort)
-
核心思想:每一轮通过相邻元素的比较和交换,将当前未排序区间的最大(或最小)元素像气泡一样逐渐"冒"到序列的末尾。
-
性能评估:
- 时间复杂度:O(n2)
- 空间复杂度:O(1)
- 稳定性:稳定,相邻的相等元素不进行交换,保持了它们的原始相对顺序
-
执行步骤:
- 外层循环控制总轮数,共进行
n-1 轮。 - 内层循环负责在当前轮次中,从头到尾比较相邻的两个元素。
- 如果前一个元素大于后一个元素,则交换它们的位置。
- 一轮结束后,未排序区间的最大值就被放置到了正确的位置。
- 外层循环控制总轮数,共进行
-
步骤示意

*(动态演示:visualgo.net/zh/sorting* )
- 代码示例
/**
* 冒泡排序示例:
* 通过不断比较相邻元素,把较大的“冒”到右侧,最终得到一个从小到大的有序数组。
*/
public class BubbleSortDemo {
public static void main(String[] args) {
// 定义并初始化一个待排序数组
int[] arr = {6, 9, 2, 9, 1};
// 记录数组长度,避免在循环里多次调用 arr.length
int n = arr.length;
/* 外层循环:决定需要进行多少轮“冒泡”
* • 第 1 轮结束后,最大的元素被挤到最右端
* • 第 2 轮结束后,次大的也就位
* • ……
* • 理论最多进行 n-1 轮即可
*/
for (int i = 1; i < n; i++) {
// flag 用来标记“本轮是否发生过交换”,若整轮都没交换,说明数组已完全有序,可提前终止
boolean flag = false;
/* 内层循环:在当前尚未排好序的区间内做相邻元素比较
* 此时右侧已有 i 个元素确定,所以 j 只需遍历到 n-i-1(所以范围就是j < n - i)
*/
for (int j = 0; j < n - i; j++) {
// 若前一个元素比后一个大,则顺序不对,需要交换
if (arr[j] > arr[j + 1]) {
int temp = arr[j]; // (1) 把较大的元素暂存
arr[j] = arr[j + 1]; // (2) 把较小的元素前移
arr[j + 1] = temp; // (3) 把较大的元素后移
flag = true; // 记录:本轮确实发生过交换
}
}
// 如果一整轮都没交换,说明数组已是升序,直接跳出外层循环
if (!flag) {
break;
}
}
System.out.println("排序后的数组:");
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
(6)选择排序(SelectionSort)
-
核心思想:每一轮从当前的未排序区间中"选择"出最小(或最大)的元素,并将其与未排序区间的第一个元素交换位置。
-
性能评估:
- 时间复杂度:O(n2)
- 空间复杂度:O(1)
- 稳定性:不稳定,找到最小(或最大)元素后与前方元素交换时,可能改变相等元素的相对顺序。
-
执行步骤:
- 外层循环控制轮数,共进行
n-1 轮。每一轮确定一个位置上的正确元素。 - 在每一轮中,假设未排序区间的第一个元素为最小,记录其索引。
- 内层循环遍历未排序区间,寻找实际最小元素的索引。
- 一轮内循环结束后,将找到的实际最小元素与未排序区间的第一个元素进行交换。
- 外层循环控制轮数,共进行
-
步骤示意:

- 代码示例
/**
* 选择排序示例:
* 每一轮从未排序区间选择最小的元素,放到已排序区间的末尾。
*/
public class TestSelectionSort {
public static void main(String[] args) {
// 定义并初始化一个待排序数组
int[] arr = {6, 9, 2, 9, 1};
// 记录数组长度
int n = arr.length;
/* 外层循环:决定需要进行多少轮选择
* • i 代表当前轮次中,最小元素应该被放置到的目标位置的索引
* • 总共需要进行 n-1 轮
*/
for (int i = 0; i < n - 1; i++) {
int minIndex = i; // 假设本轮未排序部分的第一个元素是最小的
/* 内层循环:在 arr[i+1...n-1] 这个未排序区间中找到最小元素的索引
*/
for (int j = i + 1; j < n; j++) {
if (arr[j] < arr[minIndex]) {
minIndex = j; // 更新最小元素的索引
}
}
// 如果最小元素的索引不是当前轮次的起始位置i,则交换
if (minIndex != i) {
int temp = arr[i];
arr[i] = arr[minIndex];
arr[minIndex] = temp;
}
}
System.out.println("排序后的数组:");
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k] + " ");
}
}
}
(7)插入排序(InsertionSort)
-
核心思想:将整个数组看作已排序和未排序两部分。每一轮从未排序部分取出一个元素,将其插入到已排序部分的正确位置,以维持已排序部分的有序性。就像打扑克牌时整理手中的牌。
-
性能评估:
- 时间复杂度:O(n2) (但在近乎有序的数组上效率很高,接近O(n))
- 空间复杂度:O(1)
- 稳定性:稳定
-
执行步骤:
- 默认数组第一个元素构成初始的已排序区间。
- 外层循环从未排序区间的第一个元素(即数组第二个元素)开始,逐个取出作为“待插入元素”。
- 内层循环(或while循环)将“待插入元素”与已排序区间的元素从后往前比较。
- 若已排序元素大于“待插入元素”,则将该元素后移一位。
- 重复步骤4,直到找到插入位置(即遇到一个小于或等于“待插入元素”的已排序元素,或已到达区间头部),将“待插入元素”放入该位置。
-
步骤示意:

- 代码示例:
/**
* 插入排序示例:
* 将数组分为已排序和未排序两部分,每次从未排序部分取一个元素插入到已排序部分的正确位置。
*/
public class InsertionSort {
public static void main(String[] args) {
// 定义并初始化一个待排序数组
int[] arr = {6, 9, 2, 9, 1};
// 记录数组长度
int n = arr.length;
/* 外层循环:从第二个元素开始(索引为1),逐个选取元素作为待插入元素
* i 指向当前待插入元素的索引
*/
for (int i = 1; i < n; i++) {
int currentElement = arr[i]; // 当前需要被插入到前面有序序列中的元素
int j = i - 1; // j 是指向已排序序列中最后一个元素的索引
/* 内层循环 (或者说是一个查找和移动的过程):
* 将 currentElement 与已排序序列中的元素从后向前比较
* 如果已排序序列中的元素 arr[j] 大于 currentElement,
* 则将 arr[j] 向后移动一位,为 currentElement 腾出空间
*/
while (j >= 0 && arr[j] > currentElement) {
arr[j + 1] = arr[j]; // 元素后移
j--; // 继续向前比较
}
// 当循环结束时,j+1 就是 currentElement 应该插入的位置
// (因为 j 要么变成了 -1,要么 arr[j] <= currentElement)
arr[j + 1] = currentElement; // 插入元素
}
System.out.println("排序后的数组:");
for (int k = 0; k < arr.length; k++) {
System.out.print(arr[k] + " ");
}
}
}
5、数组元素查找算法
(1)线性查找 (Linear Search)
也称为顺序查找,是最基础的查找算法。
-
核心思想:从数组的第一个元素开始,逐个向后扫描,将其与目标值进行比较。
-
适用场景:适用于任何数组,无论其是否有序。
-
执行过程:
- 如果当前元素与目标值相等,查找成功,返回当前元素的索引。
- 如果扫描完整个数组仍未找到,则查找失败。
public class TestArrayOrderSearch {
//查找value第一次在数组中出现的index
public static void main(String[] args){
int[] arr = {4,5,6,1,9};
int value = 1; //要查找的元素
int index = -1; //下标一开始初始化为-1,因为正常的下标不会是-1,所以如果最后index的值仍然是-1,那么说明要查找的元素不在此数组中
for(int i=0; i<arr.length; i++){
if(arr[i] == value){
index = i;
break;
}
}
//输出结果
if(index==-1){
System.out.println(value + "不存在");
}else{
System.out.println(value + "的下标是" + index);
}
}
}
(2)二分查找 (Binary Search)
-
核心前提:数组必须是有序的。这是使用二分查找的绝对前提。
-
核心思想:通过不断将查找范围对半分割,来快速定位目标元素。
-
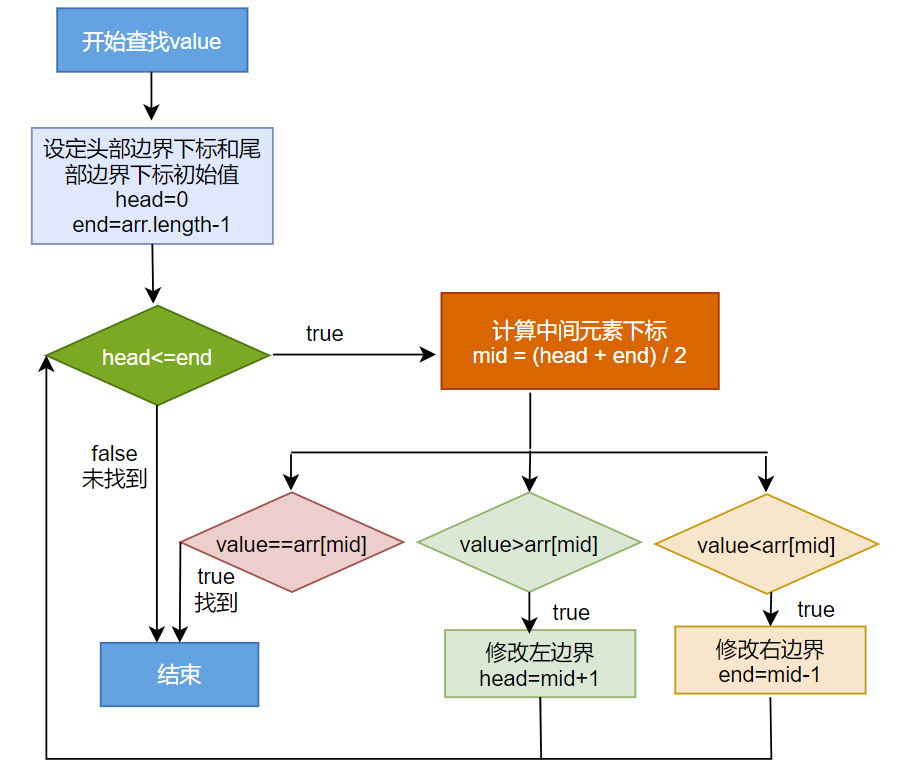
执行过程:
-
定义三个指针:
head(头部)、tail(尾部)和mid(中间)。 -
比较
arr[mid] 与目标值:- 若相等,则查找成功。
- 若
arr[mid] 小于目标值,说明目标在右半区,将head 移至mid + 1。 - 若
arr[mid] 大于目标值,说明目标在左半区,将tail 移至mid - 1。
-
重复步骤2,直到
head > tail,表示查找范围为空,查找失败。
-
/**
* 二分查找示例:
* 在一个有序数组中高效地查找目标值。
*/
public class TestBinarySearch {
public static void main(String[] args) {
int[] arr = new int[]{-99, -54, -2, 0, 2, 33, 43, 256, 999};
boolean isFlag = false; // 标记是否找到目标值,找到就设置为true
int target = 256; // 目标值
int head = 0; // 头索引
int tail = arr.length - 1; // 尾索引
// 循环条件: 头索引小于等于尾索引,因为当头索引大于尾索引时,说明数组中不存在目标值,此时循环结束
while (head <= tail) {
// 计算中间索引,head + (tail - head) 防止(tail+head) 溢出
int mid = head + (tail - head) / 2;
if (arr[mid] == target) {
System.out.println("找到目标值, 索引为: " + mid);
isFlag = true;
break;
} else if (arr[mid] < target) { // 目标值在右半部分,更新左边界
head = mid + 1;
} else { // 目标值在左半部分,更新右边界 (arr[mid] > target)
tail = mid - 1;
}
}
if (!isFlag) {
System.out.println("未找到目标值: " + target);
}
}
}
(3)查找最值
- 核心思想:采用“打擂台”的方式。先假设数组第一个元素是最大(或最小)值,然后遍历数组的其余元素,逐个与当前的“擂主”比较,如果挑战者更优,则更新“擂主”。
// 求最值及最值出现的下标
public class TestArrayExtrema {
public static void main(String[] args) {
int[] arr = {4,5,6,1,9,9,3};
//找最大值
int max = arr[0]; // 将变量 max 初始化为数组的第一个元素 arr[0]
for(int i=1; i<arr.length; i++){ // 循环查找最大值,此处i从1开始,是max不需要与arr[0]再比较一次了
if(arr[i] > max){
max = arr[i];
}
}
System.out.println("最大值是:" + max);
System.out.print("最大值的下标有:"); // 表示接下来将输出最大值的下标。
//遍历数组,看哪些元素和最大值是一样的
for(int i=0; i<arr.length; i++){
if(max == arr[i]){
System.out.print(i+"\t"); // 用制表符 \t 分隔
}
}
System.out.println();
// 找最小值
int min = arr[0];
for(int i=1; i<arr.length; i++){
if(arr[i] < min){
min = arr[i];
}
}
System.out.println("最小值是:" + min);
System.out.print("最小值的下标有:");
//遍历数组,看哪些元素和最小值是一样的
for(int i=0; i<arr.length; i++){
if(min == arr[i]){
System.out.print(i+"\t");
}
}
}
}
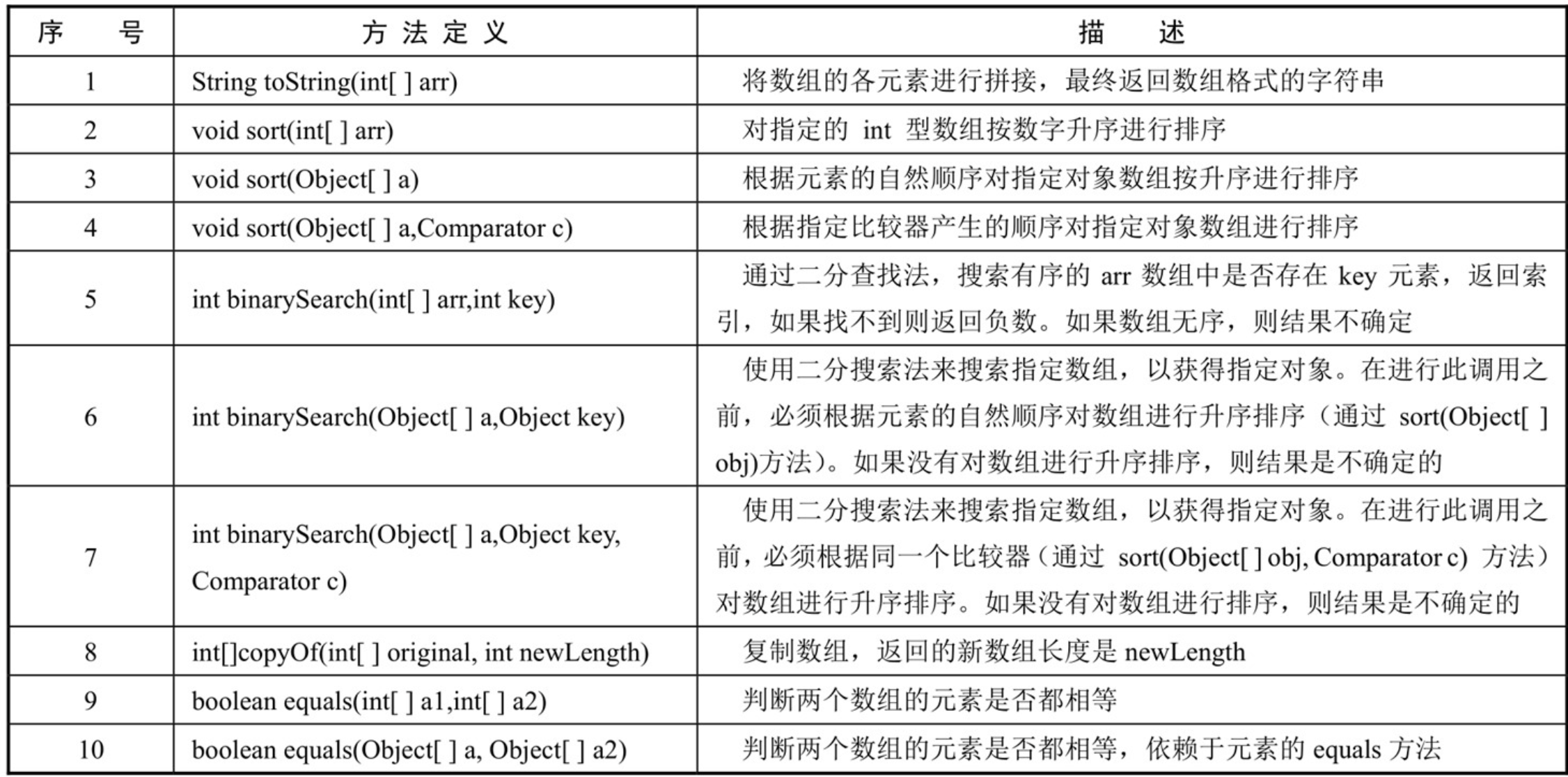
6、Arrays 工具类的使用
在实际的后端开发中,我们很少自己从头编写排序、查找等基础算法。JDK在java.util.Arrays类中为我们提供了经过高度优化的、可以直接使用的静态方法。
import java.util.Arrays;
public class ArraysUtilDemo {
public static void main(String[] args) {
int[] arr = {3, 2, 5, 1, 6};
System.out.println("排序前: " + Arrays.toString(arr)); // 使用toString()打印
Arrays.sort(arr); // 使用sort()排序
System.out.println("排序后: " + Arrays.toString(arr));
}
}
7、数组中的常见异常
(1)ArrayIndexOutOfBoundsException (数组索引越界异常)
- 触发原因:访问了不存在的索引。数组的合法索引范围是 [0, array.length - 1]。任何超出这个范围的访问都会触发此异常。
- 开发者法则:这不是一个需要用 try-catch 捕获的异常,而是一个必须修复的编码Bug。
public class ArrayIndexOutOfBoundsDemo {
public static void main(String[] args) {
int[] arr = {1, 2, 3};
// 正确访问最后一个元素
System.out.println("最后一个元素:" + arr[arr.length - 1]); // 输出: 3
// 错误示例:以下两行都会抛出 ArrayIndexOutOfBoundsException
// System.out.println(arr[3]);
// System.out.println(arr[arr.length]);
}
}
(2)NullPointerException (空指针异常)
-
触发原因:当一个引用变量的值为
null 时,尝试通过它去调用方法或访问属性(如length)。null 表示“没有指向任何对象”,自然无法进行任何操作。 -
常见场景:
- 一个数组变量被声明但从未被
new 初始化。 - 对于对象数组,数组本身已初始化,但其内部元素为
null。 - 对于二维数组,只初始化了外层数组,而内层数组为
null。
- 一个数组变量被声明但从未被
观察以下代码
public class NullPointerDemo {
public static void main(String[] args) {
// 这是导致空指针异常的典型场景(针对二维数组)
int[][] arr = new int[3][]; // 只创建了外层数组,arr[0], arr[1], arr[2] 的值都是 null
// arr[0] 的值是 null,尝试在 null 上访问索引 [0],必然导致空指针异常
System.out.println(arr[0][0]); // 触发 NullPointerException
}
}
五、多维数组
当要存储一组数据时,可以考虑使用一维数组;那么当有多组数据需要存储和处理时,就需要用到多维数组。一般来讲,二维数组就已经满足了很多场景下的需求。
二维数组实际上就是一维数组作为元素构成的新数组,里面的每个元素都是一个一维数组。我们往往将二维数组中一维数组的个数称为行数,将每个一维数组的元素个数称为列数。
在 Java 中,二维数组不一定是规则的矩阵,即每个一维数组的列数不一定一样。从数组底层的运行机制来看,其实没有多维数组。
1、声明
// 推荐方式
数组类型[][] 数组名;
// 其他等价方式
数组类型 数组名[][];
数组类型[] 数组名[];
2、初始化
(1)静态初始化
// 格式一
数据类型[][] 数组名 = new 数据类型[][]{{元素1,元素2...},{元素1,元素2...},{元素1,元素2...}};
// 格式二,简化版
数据类型[][] 数组名 = {{元素1,元素2...},{元素1,元素2...},{元素1,元素2...}};
(2)动态初始化
所谓动态初始化,是指在对数组初始化时,只是确定数组的行数和列数,甚至行数和列数都需要在程序运行期间才能确定。当确定完数组的行数和列数之后,数组的元素是默认值。
动态初始化分为两种,一种是每行的列数可以相同,另一种是每行的列数可以不同。
- 规则数组 (每一行列数相同)
//(1)确定行数和列数
//此时创建完数组,行数、列数确定,而且元素也都有默认值
数据类型[] [] 二维数组名 = new 数据类型[m] [n];
//(2)再为元素赋新值
二维数组名[行下标] [列下标] = 值;
m:表示这个二维数组有多少个一维数组。或者说二维表有几行
n:表示每一个一维数组的元素有多少个。或者说每一行共有几列
// 创建一个3行4列的二维数组
int[][] arr = new int[3][4];
- 不规则数组 (每一行列数可以不同)
//(1)先确定总行数
// 此时只是确定了总行数,每一行里面现在是null
数据类型[][] 二维数组名 = new 数据类型[总行数][];
//(2)再确定每一行的列数,创建每一行的一维数组
// 此时已经new完的行的元素就有默认值了,没有new的行还是null
二维数组名[行下标] = new 数据类型[该行的总列数];
//(3)再为元素赋值
二维数组名[行下标][列下标] = 值;
// 只指定行数
int[][] arr = new int[3][];
// 再为每一行(每个一维数组)单独开辟空间
arr[0] = new int[2]; // 第0行有2列
arr[1] = new int[3]; // 第1行有3列
arr[2] = new int[1]; // 第2行有1列
3、访问与遍历
(1)元素访问
-
二维数组长度/行数:
二维数组名.length -
**二维数组行下标的范围:**
[0, 二维数组名.length-1] (此时把二维数组看成一维数组的话,元素是行对象。) -
**二维数组某一个元素:**
二维数组名[行下标] [列下标](即先确定行/组,再确定列。) -
**二维数组某一行的列数:**
二维数组名[行下标].length(二维数组的每一行是一个一维数组。)
(2)遍历方式:嵌套循环
int[][] arr = {{1, 2}, {3, 4, 5}};
System.out.println("---- 标准for循环遍历 ----");
for (int i = 0; i < arr.length; i++) { // 遍历行
for (int j = 0; j < arr[i].length; j++) { // 遍历当前行的列
System.out.print(arr[i][j] + "\t");
}
System.out.println(); // 换行
}
System.out.println("---- 增强for循环遍历 ----");
for (int[] row : arr) { // 遍历每一行(得到一个一维数组)
for (int element : row) { // 遍历当前行中的每个元素
System.out.print(element + "\t");
}
System.out.println(); // 换行
}
// 注意:上述代码中,二维数组的索引从0开始,到数组长度-1结束。
// 另外,二维数组的遍历方式与一维数组类似,只是多了一个外层循环。