数据结构---栈&&队列
目录
[TOC]
什么是数据结构
数据结构就是在计算机中存储和组织数据的方式,我们知道计算机中的数据非常庞大,如何以高效的方式组织和存储呢,这就好比一个庞大图书馆中存储了大量的数据,我们不仅仅要把书放进去还应该在合适的时候取出来
如果自己的书相对比较少可以随意摆放,如果你有一家书店书的数量相对比较多,应该怎么放?,
图书摆放使得两个相关操作方便实现 新书怎么插入? 怎么找到某本指定的书
- 方法一哪里有空放哪里,一步到位 找某本书不方便查找
- 方法二 新进一本 《阿Q正传》,按照字母顺序找到位置插入,二分查找法
- 方法三:把书架划分成几块区域,按照类别存放,类别中按字母顺序,先定类别在二分查找
总结:解决方法的效率跟数据的组织方式有关,计算机中存储的数据相对于图书馆的书籍来说,数据更大,数据种类更多,以什么样的方式,来存储和组织我们的数据才能在使用数据时更加方便?这就是数据结构需要考虑的问题
常见的数据结构比较多
- 每一种都有其对应的应用场景,不同的数据结构的不同操作性能是不同的,
- 有的查询性能很快,有的插入速度很快,有的插入头和插入尾的速度很快
- 有的做范围查找很快,有的允许元素重复,有的不允许重复
- 在开发中如何选择,要根据具体的需求来选择
- 注意数据结构和语言无关,常见的编程语言都有直接或间接的使用上述常见的数据结构
什么是算法 Algorithm
算法的认识
不同的算法执行效率是不一样的,也就是说解决问题的过程中不仅仅数据存储方式会影响效率,算法的优劣也会影响着效率
算法的定义:一个有限的指令集,每条指令描述不依赖于语言,接受一些输入(有些情况不需要输入)产生输出,一定在有限步骤之后终止
Algorithm这个单词本意就是解决问题的方法、步骤逻辑,数据结构的实现离不开算法
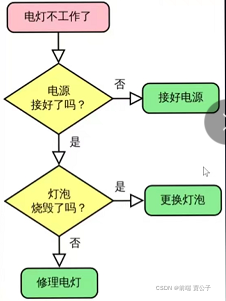
生活中的数据结构和算法
找出线缆出问题的地方
假设上海和杭州之间有一个高架桥,高架线长度时100000米,有一天其中一米出现了故障,请你想出一种算法可以快速定位到出问题的地方
线性查找:从上海的起点开始一米一米的排查,最终找到出问题的线段,但是如果线段在另一头,我们需要排查1000000次平均需要5000000次
二分查找:从中间位置开始查找,看一下问题在上海到中间的位置,还是中间到杭州的位置,查找对应的问题后,在从中间位置分开,重新锁定一般的路程,最坏的情况是20次就可以找到出现问题的地方(1000000,2)以二到底,1000000的对数约等于20
数组结构
普通语言的数组封装
- 常见的数组不能存放不同的数据类型,因此在封装时通常存放在数组中迭的是object类型
- 常见的语言数组不会自动改变(需要进行扩容操作)
- 常见语言的数组进行中间插入和删除操作性能比较低
栈结构 stack
栈也是一种非常常见的数据结构,并且在程序中的应用非常广泛
数组
- 数组是一种线性结构,并且可以在数组的任意位置插入和删除数据
- 但是有的时候我们为了实现某些功能,必须对任意性加以限制
- 而栈和队列是比较常见的受限的线性结构
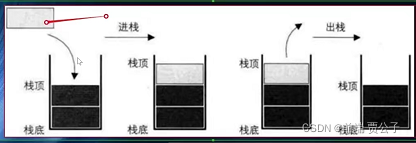
栈(stack)它是受限的线性表,先进后出(UIFO)
- 其限制是仅允许在表的一端进行插入和删除运算,这一端被称为栈顶,相对的把令一端称为栈底
- UIFO表示就是后进入的元素,第一个弹出栈空间,类似于自动餐托盘,最后放上的托盘往往先被拿出去使用
- 向一个栈插入新元素又称作进栈,入栈,或者压栈,他是把新元素放到栈顶元素的上班,使之成为新的栈顶元素
- 从一个栈删除元素右称作出栈或者退栈,他是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素
生活中类似于栈的
- 自动餐的托盘,最新放上去的,最先被客人拿走使用
- 收到很多邮件(实体的)从上往下依次处理这些邮件(最新到的邮件,最先处理)
- 注意不允许改变邮件次序,从最小开始,或者处于紧急的邮件,否则我们就不在是栈结构了,而是队列或者优先级队列结构
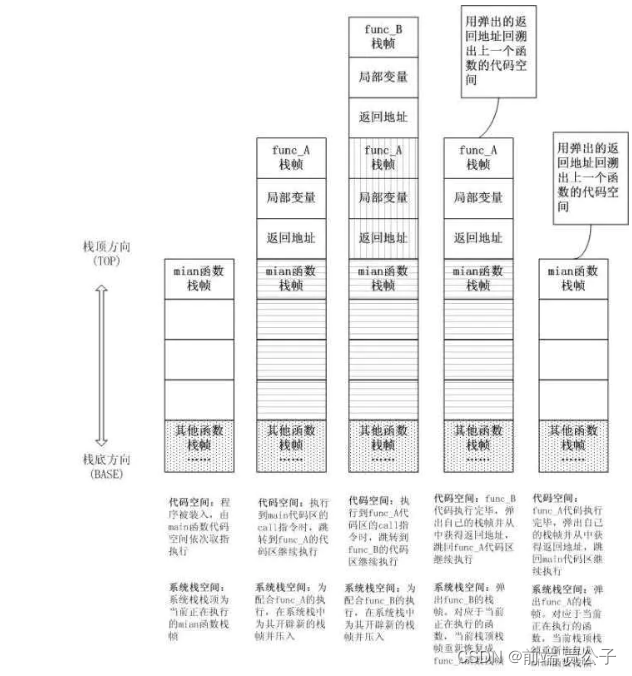
程序中什么是使用栈实现的(函数调用栈)
- 函数之间的相互调用a调用b,b调用c c调用d
- 依次入栈当前栈的顺序为a->b->c->d
- d调用完弹出栈c->b->a依次弹出栈
- 递归就是自己在调用自己只进栈,容易造成栈溢出
栈结构的实现
实现栈结构的两种比较常见的方式:基于数组实现,基于链表实现
- push //将元素压入栈
- pop从栈中取出元素
- peak查看一下栈顶元素
- isEmpty判断栈是否为空
- size 获取栈中的个数
- toString方法
// method :和某一个对象实例有联系
//封装栈类
function Stack() {
//栈中的属性
this.items = []
// 栈的相关操作
//将元素压入栈
Stack.prototype.push = function (element) {
this.items.push(element)
}
//从栈中取出元素
Stack.prototype.pop = function () {
return this.items.pop()
}
//查看一下栈顶元素
Stack.prototype.peak = function () {
return this.items[this.items.length - 1]
}
//判断栈是否为空
Stack.prototype.isEmpty = function () {
return this.items.length == 0
}
// 获取栈中的个数
Stack.prototype.size = function () {
return this.items.length
}
// toString方法
Stack.prototype.toString = function () {
let resultString = ''
for (let i = 0; i < this.items.length; i++) {
resultString += this.items[i] + ''
}
return resultString
}
}
let stack = new Stack()
十进制转二进制
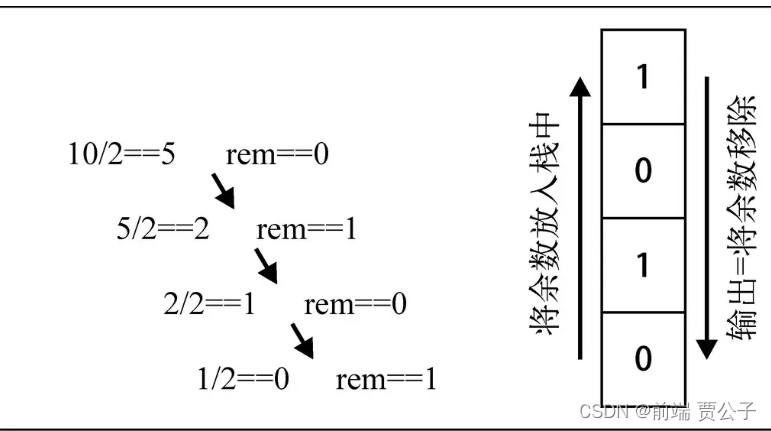
把十进制转为二进制,我们可以将十进制数字和2整除(二进制就是满二进一)
100转2进制
计算100/2余数为0。计算50/2余数为0 计算25/2余数为1.计算12/2余数为0,计算6/2余数为0 计算3/2余数为1 计算1/2余数为1 二进制结果:1100100
//将十进制转二进制
function dec2bin(decNumber) {
// 定义栈对象
var s = new Stack()
//不确定循环多少次用while循环,取出结果(作为下次的数)和余数(保存起来)
while (decNumber > 0) {
//获取余数并放到栈中
s.push(decNumber % 2)
//获取整除后的结果(向下取整),作为下次运行的结果
decNumber = Math.floor(decNumber / 2)
}
//从栈中取出0/1
let binString = ''
while (!s.isEmpty()) (
binString += s.pop()
)
return binString
}
队列结构 Queue
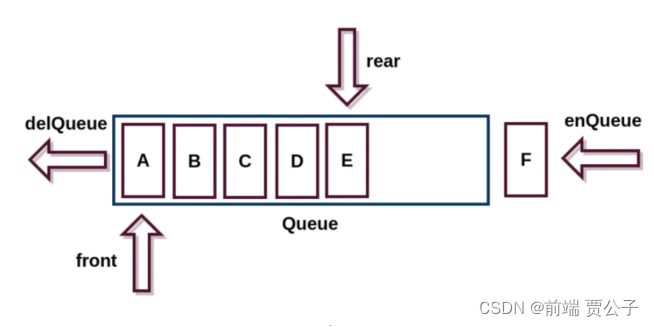
生活中类似对列的结构:电影院,商城,排队上厕所 优先排队的人优先处理
- 他是一种受限的线性表,先进先出(First in First Out)
- 受限之处在于他只允许在前端(front)进行删除操作
- 而在后端 (rear)进行插入操作
队列的应用
线程对列
- 在开发中,为了让任务可以并行处理,通常会开启多个线程
- 但是,我们不能让大量的线程同时运行处理任务(占用资源过多)
- 这个时候,如果有需要开启线程处理任务的情况,我们会使用线程队列
- 线程队列会依照次序来启动线程,并且处理对应的任务
对列类的创建
实现对列结构的两种比较常见的方式:基于数组实现,链表实现
- enter 将元素加入到对列中
- delete 从对列中删除前端元素
- front查看前端的元素
- isEmpty查看队列是否为空
- size 查看队列中元素的个数
- toString方法
<script>
// 封装队列类
function Queue() {
// 属性
this.items = []
// 队列操作的方法
// enter 将元素加入到对列中
Queue.prototype.enter = function (element) {
this.items.push(element)
}
// delete 从对列中删除前端元素
Queue.prototype.enter = function () {
return this.items.shift()
}
// 查看前端的元素
Queue.prototype.front = function () {
return items[0]
}
// 查看队列是否为空
Queue.prototype.isEmpty = function () {
return this.items.length == 0
}
// 查看队列中元素的个数
Queue.prototype.size = function () {
return this.items.length
}
// toString方法
Queue.prototype.toString = function () {
let resultString = ''
for (let i = 0; i < this.items.length; i++) {
resultString += this.items[i] + ''
}
return resultString
}
}
// 创建队列对象
let queue = new Queue()
</script>
击鼓传花面试题
几个朋友一起玩一个有戏,所有学生围成一圈,开始数数,数到某个数字的人自动淘汰,最后剩下的这个人会获得胜利,请问最后剩下的是原来那个位置上的人
思路
把所有人放到对列中,开始数数, 不是num的时候,重新加入到对列末尾, num这个数字之前的人重新放入到对列末尾,num对应这个人直接淘汰掉,获取剩下的那个人
function PassGame(nameList, num) {
//创建一个对列结构
let queue = new Queue()
//将所有人依次加入到对列
for (let i = 0; i < nameList.length; i++) {
queue.enter(nameList[i])
}
// 开始数数字,
while (queue.size() > 1) {
// 不是num的时候,重新加入到对列末尾,
// num这个数字之前的人重新放入到对列末尾
for (let i = 0; i < num - 1; i++) {
queue.enter(queue.delete())
}
// num对应这个人直接淘汰掉
queue.delete()
}
//获取剩下的那个人
alert(queue.size())
let endName = queue.front()
alert('最终剩下的人是' + endName)
return nameList.indexOf(endName)
}
names = ['lisa', 'any', 'tom', 'why', 'zs']
PassGame(names, 3)
// ['lisa', 'any', 'tom', 'why', 'zs']
// ['why,zs,lisa,any']
// ['any,why,zs']
// ['any why']
// ['why']
优先级队列
我们知道,普通的队列插入一个元素,数据会放在后端,并且需要前面所有的元素都处理完才会处理前面的数据
但是优先级队列,在插入一个元素的时候会考虑到数据的优先级,和其他的数据优先级进行比较,比较完成后,可以得出这个元素在对列中正确的位置,其他处理方式,和基本对列处理方式一样
优先级队列主要考虑的问题:每个元素不在只有一个数据,而是包含了数据的优先级,在添加方式中,根据优先级放入正确的位置
例如:登机的顺序,头等舱和商务舱的优先级高于经济舱,急诊科医生先处理病情严重的患者
计算机中,我们可以经过优先级队列来重新排序队列中的任务顺序,比如每个线程的任务重要性不同,我们可以通过优先级的大小,来决定线程在对列中被处理的次序
优先级队列的实现
封装元素和优先级放在一起,添加元素时,将新插入元素的优先级和列中已存在的优先级进行比较,以获取自己的正确位置
优先级越小越靠前 ,如果对列为空,不需要做任何比较 如果有数据,小的插入到前面,大的在后面
//封装优先级队列
function Priority() {
// 在 Priority 重新构建了一个类:可以理解成内部类
function QueueElement(element, priority) {
this.element = element//元素
this.priority = priority//优先级
}
this.items = []
// 实现插入类方法
Priority.prototype.enqueue = function (element, priority) {
let queueElement = new QueueElement(element, priority)
//判断队列是否为空
if (this.items.length == 0) {
this.items.push(queueElement)
} else {
let added = false
for (let i = 0; i < this.items.length; i++) {
if (queueElement.priority < this.items[i].priority) {
this.items.splice(i, 0, queueElement)
added = true
break
}
}
if (!added) {
this.items.push(queueElement)
}
}
}
}
let pq = new Priority()
pq.enqueue('abc', 111)
pq.enqueue('cba', 200)
pq.enqueue('nba', 50)
pq.enqueue('nba', 66)
console.log(pq)//50,66,111,200