线性代数笔记

阿七的书桌
81 阅读2分钟

向量

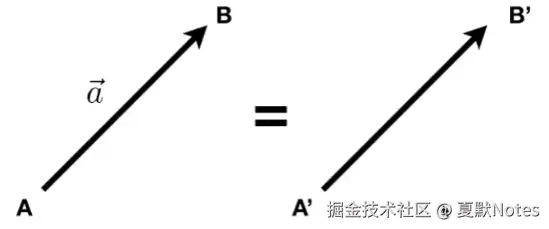
image.png

向量（vector），顾名思义，就是有方向的量，大家可以把向量理解成一条既有大小又有方向的有向线段。

向量一般有两组表示形式，一种是 a⃗\vec a，另一种则是加粗的 a\boldsymbol a。

上图为向量AB，以A点为起点，B点为终点，表示为 AB→=B−A \overrightarrow{AB} = B - A

向量表示两个内容：方向、长度

向量平移移动到不同的位置，仍然表示同一向量, A 和 B的相对位置没有改变

向量的长度：∥a⃗∥\Vert \vec a \Vert

单位向量

  • 长度为1
  • 一个向量除以自身的长度，即可得到同方向，长度为1的单位向量 a^=a⃗/∥a⃗∥\hat a = \vec a / \Vert \vec a \Vert
  • 可以用单位向量只表示一个方向

image.png

向量相加：平行四边形法则、三角形法则

image.png

通过坐标系。x 和 y可以表示任意向量

A=(xy)AT=(x,y)∥A∥=x2+y2A = \dbinom {x}{y} \qquad A^{\mathrm{T}} = (x, y) \qquad \Vert A \Vert = \sqrt {x^2 + y^2}

点乘

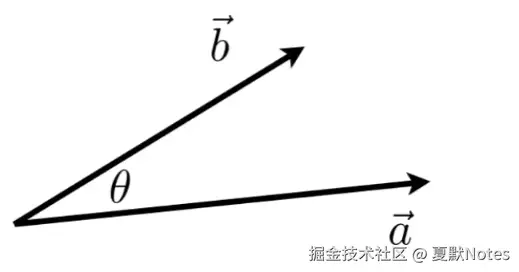
image.png

向量点乘得到的是一个数

a⃗⋅b⃗=∥a⃗∥∥b⃗∥cos⁡θ\begin{align} \vec a \cdot \vec b = \Vert\vec a\Vert \Vert\vec b \Vert \cos\theta \end{align}

在图形学中的应用：给定两个向量，可以算出夹角的余弦，即可算出两个向量之间的夹角

cos⁡θ=a⃗⋅b⃗∥a⃗∥∥b⃗∥\begin{align} \cos\theta = \frac{\vec a \cdot \vec b}{\Vert \vec a \Vert \Vert \vec b \Vert} \end{align}

当两个向量都是单位向量的时候

cos⁡θ=a^⋅b^\begin{align} \cos \theta = \hat a \cdot \hat b \end{align}

满足交换律、结合律、分配律

a⃗⋅b⃗=b⃗⋅a⃗a⃗⋅(b⃗+c⃗)=a⃗⋅b⃗+a⃗⋅c⃗(ka⃗)⋅b⃗=a⃗⋅(kb⃗)=k(a⃗⋅b⃗)\begin{align} &\vec a \cdot \vec b = \vec b \cdot \vec a \\ &\vec a \cdot (\vec b + \vec c) = \vec a \cdot \vec b + \vec a \cdot \vec c \\ &(k \vec a) \cdot \vec b = \vec a \cdot (k \vec b) = k(\vec a \cdot \vec b) \end{align}

笛卡尔坐标系下的点积，按分量相乘，然后加起来

  • 在2D中
a⃗⋅b⃗=(xaya)⋅(xbyb)=xaxb+yayb\vec a \cdot \vec b = \dbinom {x_a}{y_a} \cdot \dbinom {x_b}{y_b} = x_ax_b + y_ay_b
  • 在3D中
a⃗⋅b⃗=(xayaza)⋅(xbybzb)=xaxb+yayb+zazb\vec a \cdot \vec b = \left( \begin{matrix} x_a \\ y_a \\ z_a \end{matrix} \right) \cdot \left( \begin{matrix} x_b \\ y_b \\ z_b \end{matrix} \right) = x_ax_b + y_ay_b + z_az_b

点乘可用于计算投影

image.png

b⃗⊥\vec b_\perp：b⃗\vec b 投影到 a⃗\vec a 上

  • b⃗⊥\vec b_\perp 必须沿着 a⃗\vec a
    • b⃗⊥=ka^\vec b_\perp = k\hat a
  • k是多少
    • k=∥b⃗⊥∥=∥b⃗∥cos⁡θ k = \Vert \vec b_\perp \Vert = \Vert \vec b \Vert \cos\theta

叉积

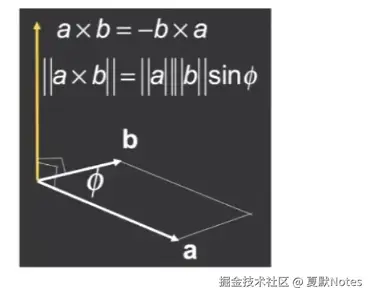
image.png

  • 叉积与两个初始向量正交（垂直）
  • 叉积出的向量垂直于两个向量所在的平面
  • 可以由右手定则确定方向
  • 可用于构建坐标系
x⃗×y⃗=+z⃗y⃗×x⃗=−z⃗y⃗×z⃗=+x⃗z⃗×y⃗=−x⃗z⃗×x⃗=+y⃗x⃗×z⃗=−y⃗\vec x \times \vec y = + \vec z \qquad \vec y \times \vec x = - \vec z \\ \vec y \times \vec z = +\vec x \qquad \vec z \times \vec y = - \vec x \\ \vec z \times \vec x = + \vec y \qquad \vec x \times \vec z = - \vec y

如果 x⃗×y⃗=+z⃗\vec x \times \vec y = + \vec z 表示右手坐标系，如果 x⃗×y⃗=−z⃗\vec x \times \vec y = - \vec z 表示左手坐标系

叉积不满足交换律

a⃗×b⃗=−b⃗×a⃗a⃗×a⃗=0⃗a⃗×(b⃗+c⃗)=a⃗×b⃗+a⃗×c⃗a⃗×(kb⃗)=k(a⃗×b⃗)\vec a \times \vec b = - \vec b \times \vec a \\ \vec a \times \vec a = \vec 0 \\ \vec a \times (\vec b + \vec c) = \vec a \times \vec b + \vec a \times \vec c \\ \vec a \times (k\vec b) = k(\vec a \times \vec b)

叉积：笛卡尔公式

a⃗×b⃗=(yazb−ybzazaxb−xazbxayb−yaxb)a⃗×b⃗=A∗b=(0−zayaza0−xa−yaxa0)=(xbybzb)\vec a \times \vec b = \left( \begin{matrix} y_az_b - y_bz_a \\ z_ax_b - x_az_b \\ x_ay_b - y_ax_b \end{matrix} \right) \\[3ex] \vec a \times \vec b = A * b = \left( \begin{matrix} 0 &-z_a &y_a \\ z_a &0 &-x_a \\ -y_a &x_a &0 \end{matrix} \right) = \left( \begin{matrix} x_b \\ y_b \\ z_b \end{matrix} \right)

叉积在图形学中的应用

  • 判断左/右
  • 判断内/外

任意三个向量组成的坐标系，满足以下三个条件，即右手坐标系

∥u⃗∥=∥v⃗∥=∥w⃗∥=1u⃗⋅v⃗=v⃗⋅w⃗=u⃗⋅w⃗=0w⃗=u⃗×v⃗\begin{align} &\Vert \vec u \Vert = \Vert \vec v \Vert = \Vert \vec w \Vert = 1 \\ &\vec u \cdot \vec v = \vec v \cdot \vec w = \vec u \cdot \vec w = 0 \\ &\vec w = \vec u \times \vec v \end{align}

可以将任意向量 p⃗\vec p 分解到三个轴上去：

p⃗=(p⃗⋅u⃗)u⃗+(p⃗⋅v⃗)v⃗+(p⃗⋅w⃗)w⃗\vec p = (\vec p \cdot \vec u)\vec u + (\vec p \cdot \vec v)\vec v + (\vec p \cdot \vec w)\vec w

矩阵

由 m x n 个数排成的m行n列的数表称为m行n列的矩阵，简称 m*n 矩阵。记作：

(135204)\left( \begin{matrix} 1 &3 \\ 5 &2 \\ 0 &4 \end{matrix} \right)

只有同型矩阵之间才可以进行加法运算，将两个矩阵相同位置的元相加即可，m行n列的两个矩阵相加后得到一个新的m行n列矩阵

矩阵相乘

前一个矩阵的列数必须等于后一个矩阵的行数，相乘才有意义：(M×N)(N×P)=(M×P)(M \times N)(N \times P) = (M \times P)

结果中元素(i ,j) 为A的第 i 行和B的 j 列的点积

矩阵的乘积

  • 没有交换律，（AB和BA一般都不同）
  • 满足结合律和分配律
    • (AB)C=A(BC)(AB)C = A(BC)
    • A(B+C)=AB+ACA(B + C) = AB + AC
    • (A+B)C=AC+BC(A + B)C = AC + BC

矩阵与向量相乘

将向量视为列矩阵（M x 1）的时候可以相乘

矩阵与向量的相乘会是转换的关键

比如：2D的图形关于y轴的镜像

(−1001)(xy)=(−xy)\left( \begin{matrix} -1 &0 \\ 0 &1 \end{matrix} \right) \left( \begin{matrix} x \\ y \end{matrix} \right) = \left( \begin{matrix} -x \\ y \end{matrix} \right)

矩阵转置

将行和列交换顺序（ij -> ji）

(123456)T=(135246)\left( \begin{matrix} 1 &2 \\ 3 &4 \\ 5 &6 \end{matrix} \right)^T = \left( \begin{matrix} 1 &3 &5 \\ 2 &4 &6 \end{matrix} \right)

性质

(AB)T=BTAT(AB)^T = B^TA^T

单位矩阵

I3×3=(100010001)AA−1=A−1A=I(AB)−1=B−1A−1I_{3 \times 3} = \left( \begin{matrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{matrix} \right) \\[3ex] AA^{-1} = A^{-1}A = I \\[3ex] (AB)^{-1} = B^{-1}A^{-1}

矩阵形式的向量乘法

点积

a⃗⋅b⃗=a⃗Tb⃗=(xayaza)(xbybzb)=(xaxb+yayb+zazb)\vec a \cdot \vec b = \vec a^T \vec b = (x_a \quad y_a \quad z_a) \left( \begin{matrix} x_b \\ y_b \\ z_b \end{matrix} \right) = (x_ax_b + y_ay_b + z_az_b)

叉积

a⃗×b⃗=A∗b=(0−zayaza0−xa−yaxa0)(xbybzb)\vec a \times \vec b = A * b = \left( \begin{matrix} 0 &-z_a &y_a \\ z_a &0 &-x_a \\ -y_a &x_a &0 \end{matrix} \right) \left( \begin{matrix} x_b \\ y_b \\ z_b \end{matrix} \right)
avatar
文章
阅读
粉丝