算法模块之链表

小小高不懂写代码
59 阅读5分钟

理论基础

链表是一种特殊的数组结构, 主要分为单向链表、双向链表、环形链表三种, 如下图所示:

链表的种类

  • 单向链表

    • 每一个节点当中, 存在一个data属性用于存放值, next属性用于指向下一个节点 单链表

  • 双向链表

    • 区别于单向链表, 多了一个prev属性用于指向前一个节点, 因此双向链表可以向前查询也可以向后查询 双向链表

  • 环形链表

    • 与双向链表类似, 区别在于形成了一个环形 循环链表

链表的存储方式

链表的节点在内存中是分散存储的，通过指针连在一起

链表的操作

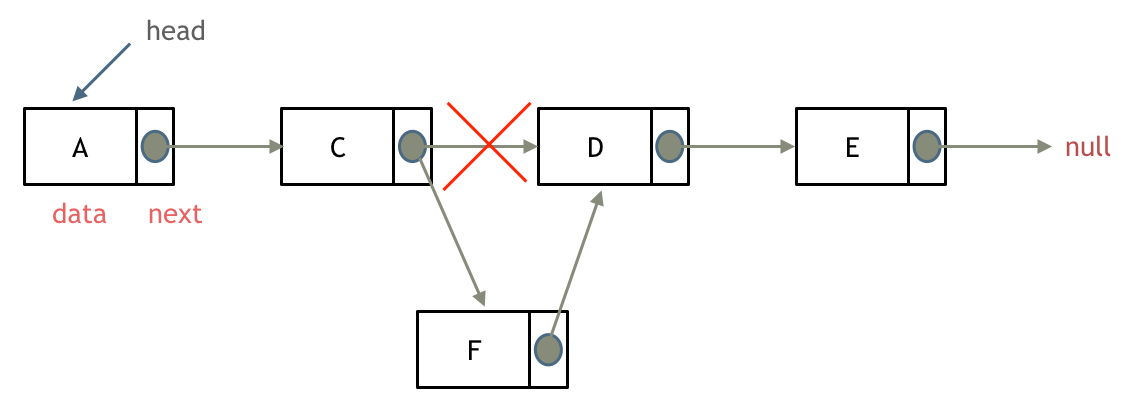
  • create: 指定索引和 value
    • 找到要添加节点的位置
    • 新增节点, 当前节点的 next 指针指向新增节点, 新增节点的 next 指针指向下一个节点
    • 添加链表
  • read: 根据指定索引找到对应节点
  • update: 指定索引和 newValue
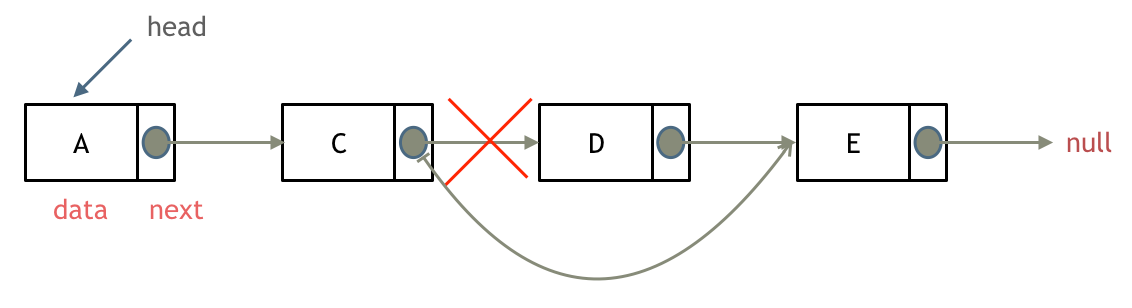
  • delete: 指定索引
    • 找到要删除的节点的前一个节点
    • 前一个节点的 next 指针指向删除节点的下一个节点
    • 需不需要将删除的节点置为 null 看编程语言, 高级语言自带垃圾清理
    • 删除链表中的某个节点

案例分析: 设计一个链表

这个作为一道经典题目, 非常适合我们去熟悉链表的整体, 我们要实现以下功能:

  • get(index): 获取链表中第 index 个节点的值。如果索引无效，则返回-1。
  • addAtHead(val): 在链表的第一个元素之前添加一个值为 val 的节点。插入后，新节点将成为链表的第一个节点。
  • addAtTail(val): 将值为 val 的节点追加到链表的最后一个元素。
  • addAtIndex(index,val): 在链表中的第 index 个节点之前添加值为 val 的节点。如果 index 等于链表的长度，则该节点将附加到链表的末尾。如果 index 大于链表长度，则不会插入节点。如果 index 小于 0，则在头部插入节点。
  • deleteAtIndex(index): 如果索引 index 有效，则删除链表中的第 index 个节点。
/**
 * 链表节点的构造函数
 */
 class LinkNode {
     constructor(data, next) {
         this.data = data;
         this.next = next;
     }
 }
 
 /**
 * 链表的构造函数
 */
 class LinkList {
     constructor() {
         this.head = null;
         this.tail = null;
         this.size = 0;
     }
     
     /**
     * @param {Number} index
     * @retusn LinkNode | null
     */
     get = (index) => {
         // 找不到对应节点
         if (index < 0 || index >= this.size) {
             return null;
         }
         let current = new LinkNode(null, this.head);
         while (index-- >= 0) {
             current = current.next;
         }
         
         return current;
     };
     
     /**
     * @param {any} value
     */
     addAtHead = (value) => {
         const node = new LinkNode(value, this.head);
         this.head = node;
         this.size++;
         if (!this.tail) {
             this.tail = node;
         }
     };
     
     /**
     * @param {any} value
     */
     addAtTail = (value) => {
         const node = new LinkNode(value, null);
         if (this.tail) {
             this.tail.next = node;
             this.tail = node;
             this.size++;
             return;
         }
         
         this.tail = node;
         this.head = node;
         this.size++;
     };
     
     /**
     * @param {any} value
     * @param {number} index
     */
     addAtIndex = (value, index) => {
         if (index > this.size) {
             return;
         }
         
         if (index === this.size) {
             return this.addAtTail(value);
         }
         
         if (index <= 0) {
             return this.addAtHead(value);
         }
         
         const prevNode = this.get(index - 1);
         const node = new LinkNode(value, prevNode.next);
         prevNode.next = node;
         this.size++;
     };
     
     /**
     * @param {number} index
     */
     deleteAtIndex = (index) => {
         if (index < 0 || index > this.size) {
             return;
         }
         
         if (index === 0) {
             this.head = this.head.next;
             this.size--;
             if (index === (this.size - 1)) {
                 this.tail = this.head;
             }
             return;
         }
         
         const prevNode = this.get(index - 1);
         prevNode.next = prevNode.next.next;
         if (index === this.size - 1) {
             this.tail = prevNode;
         }
         this.size--;
     };
 }

到这里就完成了基本的单向链表的操作了

其他案例分析

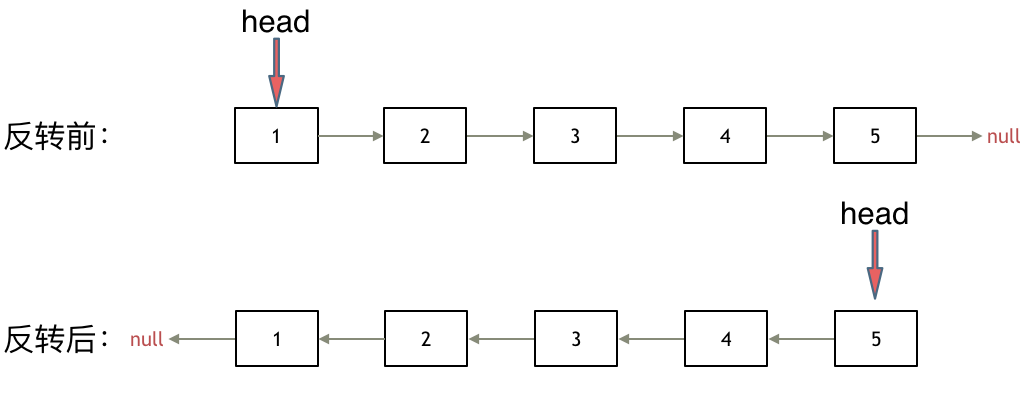
翻转链表

这道题考查的是对链表的节点操作, 这里我们用单向链表进行演示

解法一: 双指针法

翻转链表

/**
* @param {LinkNode} head 需要翻转的链表的头部
* @returns LinkNode
*/
function reserveLinkList(head) {
    if (!head || !head.next) {
        return head;
    }
    
    let [prev, current, temp] = [null, head, null];
    
    while (curren) {
        temp = current.next;
        current.next = prev;
        prev = current;
        current = temp;
    }
    
    return prev;
}

解法二: 递归

递归比较抽象, 核心思想就是一个前节点和后节点互相交换

function reserveLinkNode(prev, current) {
    if (!current) {
        return prev;
    }
    
    const temp = current.next;
    current.next = prev;
    prev = current;
    current = temp;
    
    return reserveLinkNode(prev, current);
}

function resreveLinkList(head) {
    return reserveLinkNode(null, head);
}

两两交换链表的节点

和翻转链表相似, 区别在于跨越幅度是两个节点。这里介绍个新的知识点: 虚拟头节点。一般用在需要操作头节点的场景，主要是为了减少头尾节点的判断。

function swapPairs(head) {
    let temp = new LinkNode(null, this.head);

    while (temp.next && temp.next.next) {
        const current = temp.next.next;
        const prev = temp.next;
        
        prev.next = current.next;
        current.next = prev;
        temp.next = current;
        temp = prev;
    }
    
    return temp.next;
}

链表相交

给你两个单链表的头节点 headA 和 headB ，请你找出并返回两个单链表相交的起始节点。如果两个链表没有交点，返回 null 。

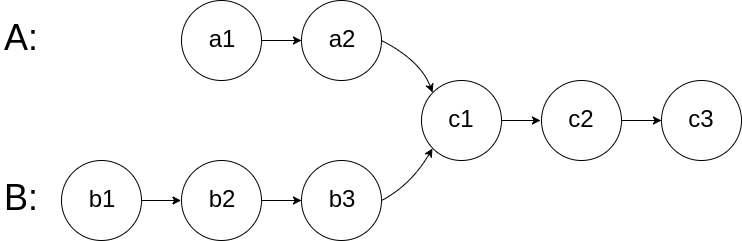
解法如下:

  1. 求出两个链表的长度
  2. 短链表移动至长链表的尾端
  3. 移动指针, 递归求出相交点
/**
* @param {LinkNode} head
* @returns number
*/
function getLength(head) {
    let current = head;
    let size = 0;
    
    while (current) {
        size++;
        current = current.next;
    }
    
    return size
}

/**
* @param {LinkNode} headA
* @param {LinkNode} headB
* @retusn LinkNode
*/
function getInstanceNode(headA, headB) {
    const sizeA = getLength(headA);
    const sizeB = getLength(headB);
    // 这里我们默认A链表是长的
    let currentA = headA;
    let currentB = headB;
    if (sizeA < sizeB) {
        [currentA, currentB] = [currentB, currentA];
        [sizeA, sizeB] = [sizeB, sizeA];
    }
    
    // 将指针移动到与B链表相同长度的地方
    let sizeDiffence = sizeA - sizeB;
    while (sizeDiffence) {
        currentA = currentA.next;
    }
    
    // 这里反向思考, 求相交点, 那么循环求不同点则跳出循环
    while (currentA && currentA !== currentB) {
        currentA = currentA.next;
        currentB = currentB.next;
    }
    return currentA;
}

删除链表的倒数第N个元素

这题是典型的双指针法, 如果不用双指针, 你就需要先计算出链表的长度, 然后得出从前往后是第几个节点, 再删除。也不是不能做～

但既然我们提起了双指针，就用双指针, 逻辑如下:

  1. 创建虚拟头节点, 方便对真实头节点进行操作
  2. 定义fast和slow指针，初始化指向虚拟头节点
  3. 先让fast指针走n+1步, 为什么是n+1呢, 是因为只有走n+1才能让slow指针指向需要删除的节点的前一个节点
  4. fast和slow同时移动, 直至fast走到末尾
  5. 删除slow指针的下一个节点
function removeNthFromEnd(head, n) {
    const virtualNode = new LinkNode(null, head);
    
    let [slowIndex, fastIndex] = [virtualNode, virtualNode];
    
    while (n--) {
        fastIndex = fastIndex.next;
    }
    
    while (fastIndex && fastIndex.next !== null) {
        slowIndex = slowIndex.next;
        fastIndex = fastIndex.next;
    }
    
    slowIndex.next = slowIndex.next.next;
    
    return virtualNode.next;
}

结语

链表大概的理论就这些, 虽然文中我使用的是单向链表, 并没有提及双向链表和环行链表, 但是大查不查, 作者也是个半吊子, 用掘金记录自己的算法成长过程, 也算是在枯燥的生活的一种慰藉吧。

avatar
文章
阅读
粉丝