DeepSeek技术解读-从MHA到MLA的完整解读（适合有点基础的同学）一、传统的多头注意力机制（MHA，Multi-

一、传统的多头注意力机制（MHA，Multi-Head Attention）：

在标准的Transformer中，多头注意力机制（MHA）通过并行计算多个注意力头来捕捉输入序列中的不同特征。每个注意力头都有自己的查询（Query, Q）、键（Key, K）和值（Value, V）矩阵，他们各自的主要作用如下：

查询矩阵 Q：查询矩阵是你想要寻找某个信息的"问题"。在Transformer中，查询矩阵是输入的一个投影，表示当前token对其他token的"需求"。它帮助你确定自己在序列中的位置和需要关注什么内容。
键矩阵 K：键矩阵是每个token提供的"信息"或"标识符"。每个token都有一个与之关联的键，用于与查询进行对比，以确定它与查询的相关性。你可以把键想象成词语的"标签"。
值矩阵 V：值是实际的信息，提供了词向量的内容。根据Q与K的匹配程度，V最终用来生成输出向量。

假定：d是隐向量维度， $n_h$ 是注意力头的数量， $d_h$ 是每个注意力头的维度， $h_t$ 是attention层地t个token的输入隐向量。

标准的MHA首先使用三个权重矩阵（训练参数） $W_q,W_k,W_v \in{\mathbb{R}^{d_h*n_h*d}}$ 计算得到 $q_t,k_t,v_t$ 向量。然后 $q_t,k_t,v_t$ 向量拆分成 $n_h$ 份（每个注意力头分一份）：

[q_{𝑡,1};q_{𝑡,2}; ...; q_{𝑡,𝑛_ℎ}]= q_𝑡 \\ [k_{𝑡,1};k_{𝑡,2}; ...; k_{𝑡,𝑛_ℎ}]= k_𝑡 \\ [v_{𝑡,1};v_{𝑡,2}; ...; v_{𝑡,𝑛_ℎ}]= v_𝑡

使用 $q_t,k_t$ 计算注意力得分，并使用注意力权重对 $v_t$ 进行加权求和，得到每个注意力头的结果：

o_{𝑡,𝑖} =\sum^{t}_{j=1}{︁Softmax_𝑗 (\frac{q^𝑇 _{𝑡,𝑖} k_{𝑗,𝑖}}{\sqrt{d_h}})} v_{j,i}

最后把所有注意力头结果向量拼接起来，通过一层限行映射回原始维度：

u_𝑡 = 𝑊^𝑂[o_{𝑡,1}; o_{𝑡,2}; ...; o_{𝑡,𝑛_ℎ}]

二、多头潜在注意力机制（MLA，Multi-Head Latent Attention) ：

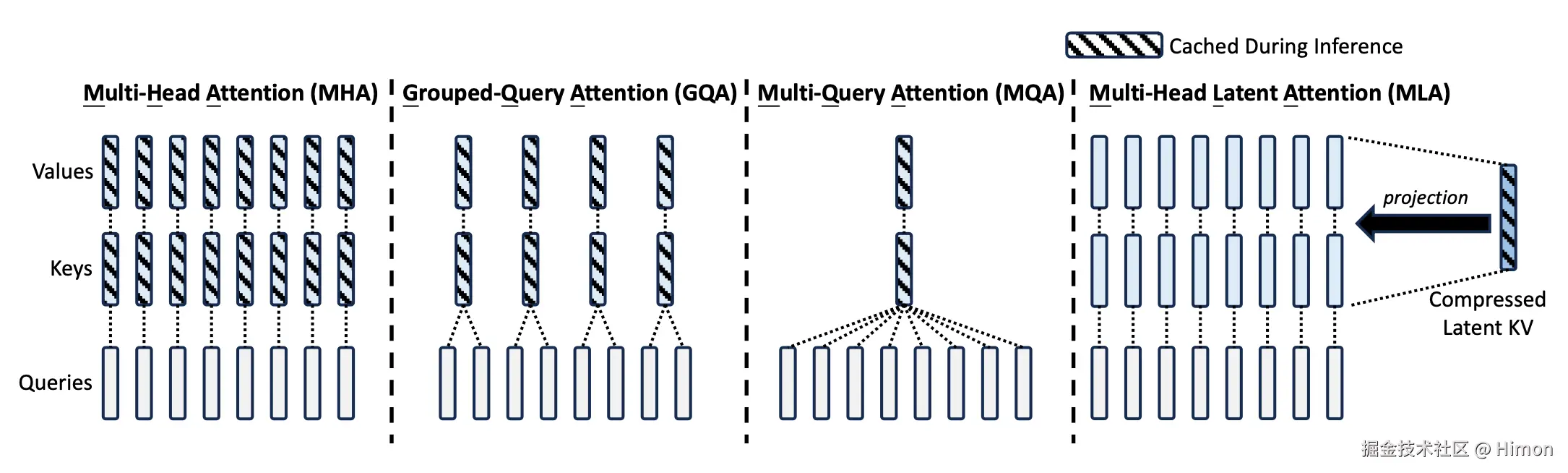
MLA的核心是对value和key进行低秩联合压缩来减少推理时的键值缓存（KV cache），MLA设计中所有的K和V都需要缓存，MLA只需要缓存一个压缩的向量，并且此向量纬度远远小于 $d_hn_h$ ，只需要在推理计算时再向上投影生成所有的K和V。具体计算如下：

2.1 对value和key进行低秩联合压缩：

具体的：

生成压缩潜在隐向量（latent vector），其中 $𝑊^{𝐷𝐾𝑉} ∈ \mathbb{R}^{𝑑_𝑐×𝑑}$ 是下投影矩阵 $c^{𝐾𝑉}_𝑡 = 𝑊^{𝐷𝐾𝑉}h_𝑡$ 。
通过上投影矩阵 $𝑊^{UK}, 𝑊^{UV} ∈ \mathbb{R}^{d_hn_h*𝑑_𝑐}$ 将潜在隐向量分别重建键K矩阵和值V矩阵，注意可以认为是映射成隐向量维度 h ，而不是每个注意力头的维度： $k^𝐶_t = 𝑊^{UK}c^{𝐾𝑉}_𝑡$ ， $v^𝐶_t = 𝑊^{UV}c^{𝐾𝑉}_𝑡$
应用旋转位置编码（RoPE），引入位置信息。因为传统的MHA中，每个token都对应着自己的K向量，天然包含了位置信息，现在通过一个共用的潜在隐向量映射得到的K是不包含位置信息的。 $k^R_t = RoPE(W^{KR}h_t)$ 。其中， $𝑊^{KR} ∈ \mathbb{R}^{𝑑^R_h*d}$ 是用于生成解耦键的矩阵， $d^R_h$ 是解耦键的维度。
将位置矩阵 $k^R_t$ 和上投影得到的矩阵 $k^C_t$ 拼接得到最终的地t个位置token的K矩阵： $k_t = [k^V_t;k^R_t]$ ， $v_t=v^C_t$ 。

因此在推理过程中，为了加速推理，需要将K、V缓存。当采用MLA：只有 $k^{KV}_t$ 和 $k^R_t$ 需要缓存，只需要缓存 $(d_c + d^R_h) * l$ 个参数。如果是MLA，所有keys和values向量都需要缓存，则需要缓存 $2n_h d_h l$ 个参数。

2.2 处理query向量

同样的，为了降低训练过程中的内存激活量，对Q也进行类似的处理:

2.3 计算attention输出

最后使用query ( $q_{t,i}$ ),keys ( $k_{j,i}$ )和values ( $v^C_{j,i}$ )计算attention结果，这里 $q_{t,i}$ 和 $k_{j,i}$ 都拼接了RoPE位置向量，所以纬度是一样的，其中 $𝑊^O ∈ \mathbb{R}^{𝑑*d_hn_h}$ 表示输出映射层矩阵，最终得到纬度为d的输出隐向量：