Let's build GPT: from scratch, in code, spelled out
《Let's build GPT:from scratch, in code, spelled out.》是 [Andrej Karpathy] 大佬录制的课程,该课程约 2 小时,从头构建出一个可工作的 GPT,Talk is Cheap,show me the Code,相当硬核。
参考
Let's build GPT:from scratch, in code, spelled out. (maxieewong.com)
Day2 - 從nanoGPT開始 (1) - iT 邦幫忙::一起幫忙解決難題,拯救 IT 人的一天 (ithome.com.tw)
Transformer通俗笔记:从Word2Vec、Seq2Seq逐步理解到GPT、BERT-CSDN博客
数据
课程中训练了一个基于字符级别的语言模型,根据前面的字符,来预测下一个字母。使用的数据集是(Tiny Shakespeare,1.06MB)。对应的 GitHub 项目是 nanoGPT。Andrej Karpathy 大佬带你,手把手,从零开始写一个 nanoGPT。
nanoGPT 也是 Andrej Karpathy 开发的开源项目,它是一个用于训练/微调中等规模 GPT 模型的最简单、最快速的方案。它是对 minGPT 的改写,更注重实用性而不是理论教育。
tokenize
tokenize 是将原始文本转化为数值表示,即 Token 序列。课程中基于字符级别的语言模型,tokenzie 算法非常简单,将所有字符排序形成一个字符表,字符的在字符表中 index 则是字符的数值
# 这里采用基于字符级别的语言模型,它的 Tokenize 算法比较简单。将上面的词汇表 (chars) 映射为整数,stoi 字符到整数的映射,itos 整数到字符的映射。encode 和 decode 分别是对字符串的编解码。
# create a mapping from characters to integers
stoi = { ch:i for i,ch in enumerate(chars) }
itos = { i:ch for i,ch in enumerate(chars) }
encode = lambda s: [stoi[c] for c in s] # encoder: take a string, output a list of integers
decode = lambda l: ''.join([itos[i] for i in l]) # decoder: take a list of integers, output a string
print(encode("hii there"))
print(decode(encode("hii there")))
结果
[46, 47, 47, 1, 58, 46, 43, 56, 43]
hii there
将自然语言文本转化为数值表示。 如何进行 tokenize 有很多高级算法,比如:google/sentencepiece(github.com/google/sent…
训练集与验证集
tokenize 后得到一个数值序列,将这个序列进行切分组合构成训练集和验证集。
训练过程是多次迭代,每次迭代的训练集和验证集称做一个 block 。所以将 token 序列进行切分,block_size 个 token 构成一个 block .
block_size = 8
train_data[:block_size+1]
x = train_data[:block_size]
y = train_data[1:block_size+1]
for t in range(block_size):
context = x[:t+1]
target = y[t]
print(f"when input is {context} the target: {target}")
这里取了训练集中的第一个 Block。block_size 大小为 8,为什么我们取了 9 个 Token 呢?
因为训练方式,将 Chunck 拆分为两个子集 x 和 y,其中 x 表示输入 Token 序列,在使用时是累增的,y 表示基于该输入,与其的输出。
when input is tensor([18]) the target: 47
when input is tensor([18, 47]) the target: 56
when input is tensor([18, 47, 56]) the target: 57
when input is tensor([18, 47, 56, 57]) the target: 58
when input is tensor([18, 47, 56, 57, 58]) the target: 1
when input is tensor([18, 47, 56, 57, 58, 1]) the target: 15
when input is tensor([18, 47, 56, 57, 58, 1, 15]) the target: 47
when input is tensor([18, 47, 56, 57, 58, 1, 15, 47]) the target: 58
为了利用 GPU 的并行计算能力,把 batch_size 个 block 组合成一个 batch 。一个 batch 是同时进入 GPU 进行计算。相互直接隔离,互不干扰。
torch.manual_seed(1337)
batch_size = 4 # how many independent sequences will we process in parallel?
block_size = 8 # what is the maximum context length for predictions?
def get_batch(split): # generate a small batch of data of inputs x and targets y
data = train_data if split == 'train' else val_data
ix = torch.randint(len(data) - block_size, (batch_size,))
x = torch.stack([data[i:i+block_size] for i in ix])
y = torch.stack([data[i+1:i+block_size+1] for i in ix]) return x, y
语言模型
语言是一套复杂的符号系统。语言符号通常在音韵(Phonology)、词法(Mor phology)、句法(Syntax)的约束下构成,并承载不同的语义(Semantics)。语言 符号具有不确定性。同样的语义可以由不同的音韵、词法、句法构成的符号来表 达;同样的音韵、词法、句法构成的符号也可以在不同的语境下表达不同的语义。 因此,语言是概率的。并且,语言的概率性与认知的概率性也存在着密不可分的关系。语言模型(LanguageModels, LMs)旨在准确预测语言符号的概率。从语 言学的角度,语言模型可以赋能计算机掌握语法、理解语义,以完成自然语言处理 任务。从认知科学的角度,准确预测语言符号的概率可以赋能计算机描摹认知、演 化智能。从 ELIZA 到 GPT-4,语言模型经历了从规则模型到统计模型,再 到神经网络模型的发展历程,逐步从呆板的机械式问答程序成长为具有强大泛化 能力的多任务智能模型。
按照语言模型发展的顺序依次基于统计方法 的n-grams 语言模型、基于循环神经网络(RecurrentNeuralNetwork,RNN)的语 言模型,基于Transformer的语言模型。
BigramLanguageModel 二元语言模型是根据前一个词,来推测下一个词,是一个经典、简单、易于理解的框架,Andrej Karpathy借助 BigramLanguageModel 先帮助我们把语言模型的大框架搭建起来。然后,在框架内,一步一步,添砖加瓦,一点点改出基于 Transformer 的 GPT
N-Gram
语言模型通过对语料库(Corpus)中的语料进行统计或学习来获得预测语言符号概率的能力。通常,基于统计的语言模型通过直接统计语言符号在语料库中 出现的频率来预测语言符号的概率。其中,N-Gram 是最具代表性的统计语言模型。N-Gram 语言模型基于马尔可夫假设和离散变量的极大似然估计给出语言符号的概率。
N-Gram 的基本思想是将文本里面的内容按照字节进行大小为N的滑动窗口操作,形成了长度是N的字节片段序列。n-grams 语言模型中的n-gram指的是长度为n的词序列。
每一个字节片段称为gram,对所有gram的出现频度进行统计,并且按照事先设定好的阈值进行过滤,形成关键gram列表,也就是这个文本的向量特征空间,列表中的每一种gram就是一个特征向量维度。
该模型基于这样一种假设,第N个词的出现只与前面N-1个词相关,而与其它任何词都不相关,整句的概率就是各个词出现概率的乘积。这些概率可以通过直接从语料中统计N个词同时出现的次数得到。常用的是二元的Bi-Gram和三元的Tri-Gram。
n-grams语言模型通 过依次统计文本中的n-gram及其对应的(n-1)-gram在语料库中出现的相对频率来 计算文本w1:N 出现的概率。计算公式如下所示:
当n=2时,称之为bigrams,其对前一个词进行考虑。此时,分子C(wi−n+1 : i) = C(wi−1,wi),C(wi−1,wi) 为词序列{wi−1,wi} 在语料库中出现 的次数;分母C(wi−n+1: i−1) = C(wi−1),C(wi−1) 为词 wi−1 在语料库中出现的次数
n-grams 具备对未知文本的泛化能力。这也是其相较于传统基于规则的方法的优势。但是,这种泛化能力会随着n的增大而逐渐减弱。
BigramLanguageModel
模型介绍
前面的 N-gram Language Model用的是统计方法建立语言模型, 但 Bigram Language Model 是使用 NN 的方法建立语言模型
课程则是从实现一个二元语言模型(BigramLanguageModel) 开始,该模型是根据当前字符推测下一个字符。模型只包含一层 (nn.Embedding)
# 二元语言模型实现
class BigramLanguageModelV1(nn.Module):
# 每个词直接从一个查找表中获取下一个词的logits值
# logits是模型做出预测前的一组未经归一化的分数,反映了不同结果的相对可能性
# an Embedding module containing vocab_size tensors of size vocab_size
self.token_embedding_table = nn.Embedding(vocab_size, vocab_size)
nn.Embedding 类 是 PyTorch 框架中用于词嵌入的一个模块。它接受两个参数:vocab_size(词汇表大小)和嵌入的维度。在这个例子中,嵌入的维度被设置为与词汇表的大小相同,这意味着每个词都会被映射到一个与整个词汇表大小相同的向量中。
nn.Embedding :

词嵌入 token embedding
词嵌入跟前面的 Tokenize 有什么区别?Tokenize 也是一种将词语转化为计算机可以理解的数值关系。
Tokenize 是基于词汇表,对自然语言进行编码。这种编码不带有语义信息。而词嵌入,是对编码后的 Token 经过 Embedding 层大量语料的训练,得到对应的词向量。经过语料训练后,词向量中带有语义信息。
语义的一种体现是,两个词向量之间的距离,表示了他们之间的相关性。最经典的案例是,词向量还有一个神奇的特性:它不仅可以反映语义上的相似性,还能利用两个向量的差来反映语义中的抽象关系。例如,词向量有一个著名的公式:女人 - 男人 = 皇后 - 国王。
模型训练
GPT 模型训练是累增训练,一次迭代训练 block 中的 token ,第一次用一个 token ,第二次用两个 token, 依次累增。
BigramLanagerModel 模型是给出一个 token 预测下一个 token, 与实际下一个 token 比较,进行学习。在模型结构介绍中,可知声明了一个 nn.Embedding 层,那如何使用其预测下一个 token 呢?首先分析一下具体的训练过程。
损失函数
# 二元语言模型实现
class BigramLanguageModelV1(nn.Module):
# 模型前向传播
# idx:即前面的 x,表示输入数据,词在词汇表中的索引的向量
# targets:训练的目标输出,比如正确的下一个词的索引
def forward(self, idx, targets=None):
# idx and targets are both (B,T) tensor of integers
logits = self.token_embedding_table(idx) # (B,T,C)
if targets is None:
loss = None
else:
B, T, C = logits.shape
logits = logits.view(B*T, C)
targets = targets.view(B*T)
loss = F.cross_entropy(logits, targets)
return logits, loss
# get device
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
# create model
m = BigramLanguageModelV1(vocab_size).to(device)
logits, loss = m(xb.to(device), yb.to(device))
print(logits.shape)
print(loss)
torch.Size([32, 65])
tensor(5.0364, grad_fn=<NllLossBackward0>)
idx 和 targets 的 shape 是 (B, T), B 是 batch_size , T 是 block_size 。
nn.Embedding 层的声明的 shape 是 (vocab_size, vocab_size), 因此 idx 中的每个元素字符可以从 token_embedding_table 中查表获得一个 vocab_size 维度的向量(这里的从 embedding_table 查表等同于激活函数计算)。 所以 logits 的 shape 是 (B, T, C) , C 是 vocab_size.
接下来使用 PyTorch 的 cross_entropy 函数来计算交叉熵误差:
这个函数会在内部进行以下操作:
- 对 logits 应用 softmax 函数,得到每个词的预测概率。
- 对每个位置,取出目标词的预测概率。
- 对这些概率取负对数,得到交叉熵损失。
- 对所有位置的交叉熵损失取平均,得到最终的损失值。
将 B 与 T 两个维度合并, logits shape 调整为 (B * T, C), targets shape 调整为 (B * T)。这样做的目的是将每个位置的预测和目标都看作是独立的样本。进行交叉熵误差计算,获得下一个 token 的概率。
交叉熵误差(Cross-Entropy Loss,简称CE)是一种常用的损失函数(loss function),尤其在机器学习和深度学习中的分类问题。它是用来衡量模型预测概率分布与真实概率分布之间的相似度。交叉熵误差的值越小,表示模型预测的概率分布与真实概率分布越接近,模型的性能越好。交叉熵损失衡量的是模型的预测与真实目标之间的差异。如果模型对正确的下一个词给出了高概率,那么损失就会很低;反之,如果模型给出了错误的预测,损失就会很高。
训练代码
# 8. 训练
# create a PyTorch optimizer
optimizer = torch.optim.AdamW(m.parameters(), lr = 1e-3)
from tqdm import tqdm
for steps in tqdm(range(10000)): # increase number of steps for good results...
# sample a batch of data
xb, yb = get_batch('train')
# evaluate the loss
logits, loss = m(xb.to(device), yb.to(device))
optimizer.zero_grad(set_to_none=True)
loss.backward()
optimizer.step()
在训练过程中,我们的目标就是最小化这个交叉熵损失。PyTorch 的优化器(如 Adam)会自动计算损失对模型参数的梯度,并根据梯度更新模型参数,使损失逐步降低。
这个过程会反复进行多个 epoch,直到模型在验证集上的性能不再提升。这意味着模型已经学会了根据上下文预测下一个词。
所以,交叉熵损失是连接模型预测和真实目标的桥梁。它提供了一种衡量模型性能的方法,并指引模型通过梯度下降来学习和改进。
注意力机制 Attention
自注意力 Self-Attention 是指序列内部的注意力计算。在自注意力中,Query、Key、Value 矩阵都来自同一个输入序列。也就是说,序列中的每个位置都要和序列中的每个位置(包括自己)计算注意力。这使得序列中的每个位置都能够“关注”到序列中的任意一个位置。通过自注意力,模型能够学习序列内部的依赖关系,捕捉序列的内部结构。
Masked Self-Attention 是 Self-Attention 的一个变种,它通过应用一个掩码(mask)来限制元素间的注意力分布。在处理序列数据(如文本或时间序列)时,有时我们希望模型在计算注意力权重时只考虑当前位置之前的元素(或特定范围内的元素),以保持信息流的方向性或遵循特定的顺序。这就是掩码发挥作用的地方。
交叉注意力 Cross-Attention 则是在两个不同序列之间进行注意力计算。在交叉注意力中,Query 矩阵来自一个序列(通常称为“目标序列”),而 Key 和 Value 矩阵来自另一个序列(通常称为“源序列”)。这使得目标序列中的每个位置都能够"关注"到源序列中的任意一个位置。通过交叉注意力,模型能够学习两个序列之间的对应关系,实现信息的传递和融合。
多头注意力
对 BigramLanguageModel 进行 Attension 改造。
Head
class Head(nn.Module):
""" 单头自注意力机制 """
def __init__(self, head_size):
super().__init__()
# 定义 key, query, value 的线性变换
# 这里的线性变换相当于将输入 x 映射到 key, query, value 空间
# 映射的维度由 head_size 定义,通常 head_size = n_embd // n_head
self.key = nn.Linear(n_embd, head_size, bias=False)
self.query = nn.Linear(n_embd, head_size, bias=False)
self.value = nn.Linear(n_embd, head_size, bias=False)
# 定义注意力掩码矩阵的上三角矩阵
# 这个矩阵用于在计算注意力时,屏蔽掉后面的位置,实现因果注意力
# 这里使用 register_buffer 是为了将这个矩阵注册为模型的一部分,但不作为参数进行优化
self.register_buffer('tril', torch.tril(torch.ones(block_size, block_size)))
# dropout 层,用于在训练时随机丢弃一部分注意力权重,提高模型的泛化能力
self.dropout = nn.Dropout(dropout)
def forward(self, x):
# x 的维度: (batch_size, seq_length, n_embd)
B,T,C = x.shape
# 计算 key, query, value
# k, q, v 的维度: (batch_size, seq_length, head_size)
k = self.key(x) # (B,T,C)
q = self.query(x) # (B,T,C)
# 计算注意力分数 (attention scores)
# 这里先计算 q 和 k 的点积,然后除以 head_size 的平方根进行缩放
# 这个缩放操作是为了让注意力分数的方差在不同的 head_size 下保持稳定
# wei 的维度: (batch_size, seq_length, seq_length)
wei = q @ k.transpose(-2,-1) * C**-0.5 # (B, T, C) @ (B, C, T) -> (B, T, T)
# 应用注意力掩码
# 这里使用 masked_fill 函数,将 tril 矩阵中为 0 的位置 (代表要被屏蔽的位置)
# 在 wei 中对应位置的值设置为负无穷大
# 这样在计算 softmax 时,这些位置的注意力分数就会变成 0
# 这实现了因果注意力,即每个位置只能 attend to 它前面的位置
wei = wei.masked_fill(self.tril[:T, :T] == 0, float('-inf')) # (B, T, T)
# 对注意力分数应用 softmax,得到注意力权重
wei = F.softmax(wei, dim=-1) # (B, T, T)
# 应用 dropout
wei = self.dropout(wei)
# 根据注意力权重聚合值 (value)
# v 的维度: (batch_size, seq_length, head_size)
v = self.value(x) # (B,T,C)
# 注意力加权求和
# out 的维度: (batch_size, seq_length, head_size)
out = wei @ v # (B, T, T) @ (B, T, C) -> (B, T, C)
return out
注意力计算公式
将输入 X 分别与权重矩阵 Wq, Wk, Wv 矩阵相乘 (B, T, C) @ (C, head_size) ,得到 query,key,value 三部分,即将输入{x1,x2,...,xt}编码为 {(q1, k1,v1), (q2,k2,v2),..., (qt, kt, vt)}。
其中,query 和 key 的转置矩阵相乘 query @ key.transpose(-2, -1) # (B, T, C) @ (B, C, T) ---> (B, T, T) 得到注意力分数,代表一个 query(每行) 与 每一个 key(每行) 的相关性得分。再使用 softmax 进行归一化,并且在归一化之前通过除以 dk 来实现,其中 dk 是head_size。这个操作确保了当head_size很大时,点积结果的方差大约是1,从而缩小了Softmax输入的值域,最后获得注意力权重矩阵 wei
value 则是对输入的编码,用这些权重矩阵 wei 对值矩阵 V 进行加权求和,得到注意力输出
注意力的头含义: nn.Linear(n_embd, head_size, bias=False) 则是一个线性层将 n_embd 维度的 x 映射到 head_size 维度的 Query, Key, Value 空间。映射的维度由 head_size 定义,通常 head_size = n_embd / n_head, n_head 为 1 时表示单头注意力,大于 1 时为多头注意力
总结
在自然语言处理任务中,注意力机制的作用与之类似。当我们处理一个句子或一段文本时,其中某些词或短语通常比其他部分更重要,包含了更多的信息。注意力机制允许模型去学习如何区分重要的信息和次要的信息,并根据这些重要的信息来做出判断或预测。
具体来说,注意力机制的核心思想可以用"查询-键-值(Query-Key-Value)"的框架来描述:
- 查询(Query):我们想要关注的内容。在自然语言处理任务中,查询通常是我们当前正在处理的词或句子。
- 键(Key):我们用来判断其他信息是否重要的参考。键可以是句子中的其他词,或者是来自其他来源的信息。
- 值(Value):我们想要提取的信息。值通常与键是一一对应的。
注意力机制的过程可以概括为:对于每个查询,我们用它去和所有的键进行比较,计算出每个键与查询的相关性或重要性。然后,我们用这些重要性作为权重,对相应的值进行加权求和,得到最终的注意力结果。这个结果就是模型认为对于当前的查询最重要的信息。
通过这种方式,注意力机制使模型能够动态地调整对不同部分信息的关注,从而更好地理解和处理复杂的语言数据。
层规范化 (Normalization)
Normalization:规范化或标准化,就是把输入数据X,在输送给神经元之前先对其进行平移和伸缩变换,将X的分布规范化成在固定区间范围的标准分布。
Normalization 的作用很明显,把数据拉回标准正态分布,因为神经网络的Block大部分都是矩阵运算,一个向量经过矩阵运算后值会越来越大,为了网络的稳定性,需要及时把值拉回正态分布。用以加速神经网络训练过程并取得更好的泛化性能。
Normalization根据标准化操作的维度不同可以分为batch Normalization和Layer Normalization,不管在哪个维度上做noramlization,本质都是为了让数据在这个维度上归一化,因为在训练过程中,上一层传递下去的值千奇百怪,什么样子的分布都有。BatchNorm就是通过对batch size这个维度归一化来让分布稳定下来。LayerNorm则是通过对Hidden size这个维度归一化来让某层的分布稳定。
BatchNorm是对一个batch-size样本内的每个特征做归一化,LayerNorm是对每个样本的所有特征做归一化。所以BN抹杀了不同特征之间的大小关系,但是保留了不同样本间的大小关系;LN抹杀了不同样本间的大小关系,但是保留了一个样本内不同特征之间的大小关系。
RNN 或Transformer为什么用Layer Normalization?,因为RNN或Transformer解决的是序列问题,一个存在的问题是不同样本的序列长度不一致,而Batch Normalization需要对不同样本的同一位置特征进行标准化处理,所以无法应用。其次BN抹杀了不同特征之间的大小关系;LN是保留了一个样本内不同特征之间的大小关系,这对NLP任务是至关重要的。对于NLP或者序列任务来说,一条样本的不同特征,其实就是时序上的变化,这正是需要学习的东西自然不能做归一化抹杀,所以要用LN。
设输入向量为 v={vi}。LN 将在v的每一维度vi上都进行归一化操作
手写 LN
class LayerNorm1d: # (used to be BatchNorm1d)
def __init__(self, dim, eps=1e-5, momentum=0.1):
self.eps = eps
self.gamma = torch.ones(dim)
self.beta = torch.zeros(dim)
def __call__(self, x):
# calculate the forward pass
xmean = x.mean(1, keepdim=True) # batch mean
xvar = x.var(1, keepdim=True) # batch variance
xhat = (x - xmean) / torch.sqrt(xvar + self.eps) # normalize to unit variance
self.out = self.gamma * xhat + self.beta
return self.out
def parameters(self):
return [self.gamma, self.beta]
LN在PyTorch中的实现
- normalized_shape:(int/list/torch.Size)该层的特征维度,即要被标准化的维度。
- eps:分母修正项。
- elementwise_affine:是否需要affine transform
torch.nn.LayerNorm(normalized_shape, eps=1e-05, elementwise_affine=True, device=None, dtype=None)
全连接前馈层(Fully-connected Feedforwad Layer)
按照推理过程中信号流转的方向,神经网络的正向传播范式可分为两大类:
- 前馈传播范式:在前馈传播范式中,计算逐层向前,“不走回头路”。采用前馈传播范式的神经网络可以统称为前馈神经网 络(Feed-forward Neural Network,FNN)。FNN 想要做到对信息进行全局考虑,则需要将所有元素同时输入到模型中去,这将导致模型参数量的激增。
- 循环传播范式:在循环传播范式中,某些层的计算结果会通过环路被反向引回前面的层中,形 成“螺旋式前进”的范式。采用循环传播范式的神经网络被统称 为循环神经网络(RecurrentNeuralNetwork, RNN)。RNN的结构可以让其在参数量不扩张的实现对全局信息的考虑,但是这样的环路结构给RNN的训练带来了挑战。在训练RNN时,涉及大量的矩阵联乘操作,容易引发梯度衰减或梯度爆炸问题。 由于RNN模型循环迭代的本质,其不易进行并行计算,导致其在输入序列较 长时,训练较慢。
全连接前馈层占据了Transformer近三分之二的参数,掌管着Transformer模型 的记忆。其可以看作是一种Key-Value模式的记忆存储管理模块。
全连接前馈 层包含两层,两层之间由ReLU作为激活函数。设全连接前馈层的输入为v,全连 接前馈层可由下式表示:
FFN(v) = max(0, (W1@V + b1))(W2 + b2)。
其中,W1和W2分别为第一层和第二层的权重参数,b1和b2分别为第一层和第二 层的偏置参数。其中第一层的可看作神经记忆中的key,而第二层可看作value
class FeedFoward(nn.Module):
""" a simple linear layer followed by a non-linearity """
def __init__(self, n_embd):
super().__init__()
self.net = nn.Sequential(
nn.Linear(n_embd, 4 * n_embd),
nn.ReLU(),
nn.Linear(4 * n_embd, n_embd),
nn.Dropout(dropout),
)
def forward(self, x):
return self.net(x)
前馈层作用
线性层+Softmax
模型的最后一层将解码器生成的向量映射到logits向量中。最后一层是一个简单的全连接神经网络,logits 是指全连接层的原始输出值,尚未经过归一化处理。
所以 logit 原本是一个函数,但在机器学习中,logits 通常就是最后一层全连接层的输出
全连接层的计算是简单的矩阵乘法运算(y = Wx + b),也称之为线性运算,这样我们可以称为线性层。
在PyTorch中,nn.Linear 是一个用于创建线性层的类。它的构造函数如下
class torch.nn.Linear(in_features, out_features, bias=True)
参数说明:
- in_features: 输入特征的数量,即输入向量的维度。
- out_features: 输出特征的数量,即输出向量的维度。
- bias(可选,默认为True):是否包含偏置项 b
但是线性层的特征表达能力是有限的,所以在这些线性计算之后又引入了非线性计算,增强模型特征的表达能力,也就是激活层,也称为非线性层。这里就列几个激活函数
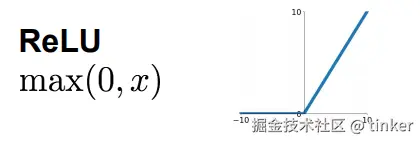
创建一个线性层将前馈层的输出 n_embd 维度的向量线性变化层 vocab_size (词表大小) 维度。每一个维度对应一个 token 的得分。
self.lm_head = nn.Linear(n_embd, vocab_size)
所以最后计算出序列 (B, T, n_embd) 中每一项的下一个 token 的得分的序列 (B, T, vocab_size)
这些得分转化为实际的概率,需要应用 softmax 函数:
probs = F.softmax(logits, dim=-1) # (B, T, vocab_size)
softmax 函数将这些得分转化为正数,并且保证它们的和为 1,因此可以被解释为概率。
有了这个概率分布,就可以进行实际的预测了。最简单的方法是选择概率最大的 Token:
next_token = torch.argmax(probs, dim=-1) # (B, T)
这给了下一个最可能的 Token。但是,这种贪心的方法可能会导致生成的文本缺乏多样性。一种更好的方法是从概率分布中随机采样:
next_token = torch.multinomial(probs, num_samples=1) # (B, T, 1)
这种方法允许模型生成多样化的文本,虽然可能不总是选择概率最大的 Token
next_token 是多个 token, 不是一个。
如果是给定一句话,预测下一个 Token 来说,实际上只需要序列的最后一个 logit 得分向量,对其采样即可。
# logits 的形状:(B, T, vocab_size)
# 取出最后一个时间步的 logits,形状变为 (B, vocab_size)
logits = logits[:, -1, :]
# 应用 softmax 得到概率分布,形状为 (B, vocab_size)
probs = F.softmax(logits, dim=-1)
# 从概率分布中采样,得到下一个 token,形状为 (B, 1)
next_token = torch.multinomial(probs, num_samples=1)
next_token 只是一个 token。每次都将新生成的 Token 附加到上下文的末尾,重复生成过程,我们就可以让模型生成一段连贯的文本。