概率分布复习：因果推断的统计学基础因果推断建模流程里，构建好了贝叶斯网络结构图，下一步是要做贝叶斯网络的概率计算。概率计

因果推断建模流程里，构建好了贝叶斯网络结构图，下一步是要做贝叶斯网络的概率计算。概率计算环节，往往会涉及到一些经典的概率分布，这篇文章主要是为了复习下常用的概率分布。

Bernoulli Distribution（伯努利分布）

考虑把1个小球(1个随机变量)，放入2个箱子的概率。若小球在箱子1的概率为 $p$ ，则小球在箱子2的概率为 $1-p$ 。

Categorical Distribution（类别分布）

考虑把1个小球(1个随机变量 $x$ )，放入 $K$ 个箱子的概率。若小球在箱子 $k$ 的概率为 $\theta_{k}$ ，即 $P(x_k=1)=\theta_k$ ，其中 $\sum_{k=1}^k\theta_k=1$ 。故，

p(x|\theta)=\prod_{k=1}^K\theta_k^{x_k}

Multinomial Distribution （多项分布）

考虑把 $N$ 个小球( $N$ 个随机变量)，放入 $K$ 个箱子的概率。若小球在箱子 $k$ 的概率为 $\theta_{k}$ ，其中

\sum_{k=1}^K\theta_k=1

$N$ 个小球可以看成 $N$ 个独立的观测变量 $\mathcal{D}=\{x_1,x_2,\ldots,X_N\}$ ，则 $N$ 个小球的分布

p(\mathcal{D}|\theta)=\frac{N!}{m_1!\ldots m_K!}\prod_{k=1}^K\theta_k^{m_k}

其中， $m_1$ 表示在箱子1内的小球数，...， $m_K$ 表示在箱子 $K$ 内的小球数，概率即为 $C_N^{m_1}C_{N-m_1}^{m_2}\ldots C_{m_k}^{m_k}\theta_1^{m_1}\theta_2^{m_2}\ldots\theta_K^{m_K}$ 其中， $C_N^{m_1}C_{N-m_1}^{m_2}\ldots C_{m_k}^{m_k}$ 表示，从 $N$ 个小球里选 $m_1$ 个放到箱子1，从 $N-m_{1}$ 个小球里选 $m_2$ 个放到箱子2...化简过程，如下：

C_N^{m_1}C_{N-m_1}^{m_2}\ldots C_{m_k}^{m_k}=\frac{N!}{m_1!(N-m_1)!}\frac{(N-m_1)!}{m_2!(N-m_1-m_2)!}\ldots

公众号原文概率分布复习：因果推断的统计学基础

Dirichlet Distribution（狄利克雷分布）

Dirichlet分布，如下：

Dir(\theta|\alpha)=\frac{\Gamma(\sum_{k=1}^K\alpha_k)}{\Gamma(\alpha_1)\ldots\Gamma(\alpha_K)}\prod_{k=1}^K\theta_k^{\alpha_k-1}

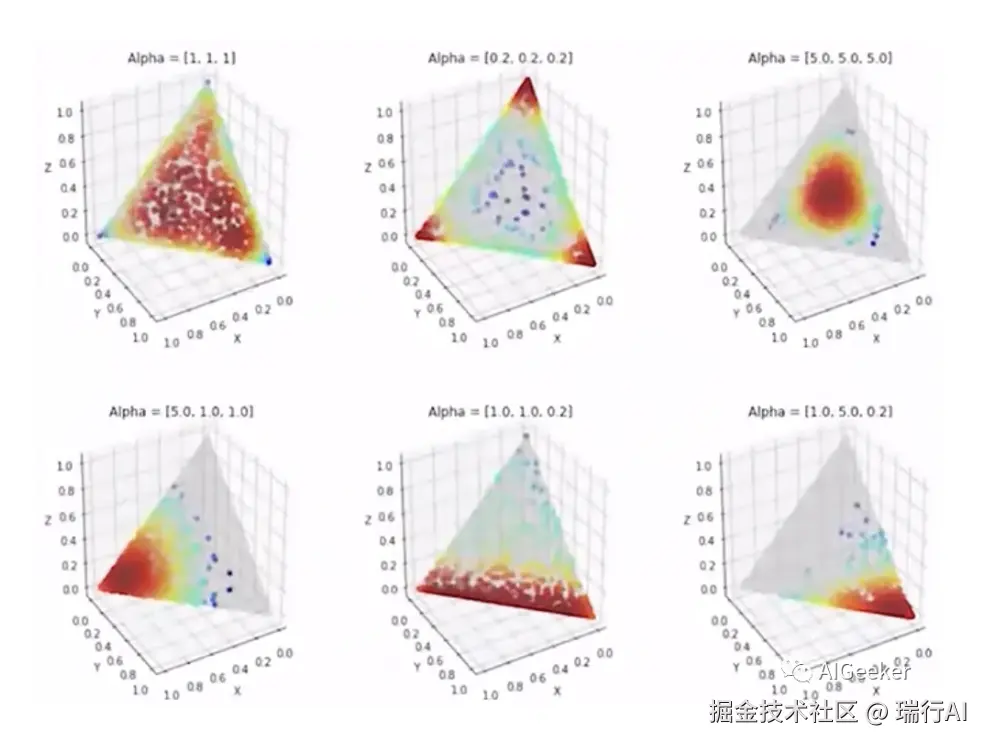
其中， $\theta_{k}$ 是 $k$ 维随机变量， $\sum_{k=1}^K\theta_k=1,\theta_k\geq0\mathrm{~;~}\alpha$ 是 $k$ 维参数，每一维都是非负的。下图是 $k=3$ 时，不同 $\alpha_1,\alpha_2,\alpha_3$ 取值组合，对应的 $\theta$ 分布：

贝叶斯公式

p(\theta|x)=\frac{p(x|\theta)p(\theta)}{p(x)}

其中， $p(\theta|x)$ 是后验分布， $p(x|\theta)$ 是似然函数， $p(\theta)$ 是先验分布。

（1）似然分布：

p(\mathcal{D}|\theta)=\prod_{i=1}^Np(x_i|\theta)=\prod_{i=1}^N\prod_{k=1}^K\theta_k^{x_{i,k}}=\prod_{k=1}^K\theta_k^{\sum x_{i,k}}=\prod_{k=1}^K\theta_k^{m_k}

（2）先验分布 $p(\theta)$ 是每个小球被放入每个箱子的概率， $p(x_i|\theta)$ 服从Categorical Distribution的， $\theta=(\theta_1,\theta_2,\ldots,\theta_K)$ 的每个维度 $\theta_{k}$ 表示小球被放入第 $k$ 个箱子的概率，满足 $\sum_{k=1}^K\theta_k=1$ ，其中 $\theta_{k}\geq0$ 。

可以假设 $\theta=(\theta_1,\theta_2,\ldots,\theta_K)$ 服从Dirichlet Distribution，也就是

p(\theta|\alpha)=Dirichlet(\theta|\alpha)=C(\alpha)\prod_{k=1}^K\theta_k^{\alpha_k-1}

根据贝叶斯公式，对单个观察变量有 $p(\theta|x,\alpha)\propto p(x|\theta)p(\theta|\alpha)$ ，则对全部观测变量有 $p(\theta|\mathcal{D},\alpha)\propto p(\mathcal{D}|\theta)p(\theta|\alpha)$ ：似然分布

p(\mathcal{D}|\theta)=\prod_{k=1}^K\theta_k^{m_k}\sim Dirichlet(m)

是Dirichlet Distribution；先验分布

p(\theta|\alpha)=C(\alpha)\prod_{k=1}^K\theta_k^{\alpha_k-1}

根据贝叶斯公式，可得后验分布

p(\mathcal{D}|\theta)p(\theta|\alpha)=\prod_{k=1}^K\theta_k^{m_k}\cdot C(\alpha)\prod_{k=1}^K\theta_k^{\alpha_k-1}\propto\prod_{k=1}^K\theta_k^{\alpha_k+m_k-1}

服从Dirichlet Distribution，即

\prod_{k=1}^K\theta_k^{\alpha_k+m_k-1}\sim Dirchilet(\alpha+m)

公众号原文概率分布复习：因果推断的统计学基础

Gamma Distribution（伽马分布）

Gamma函数

Beta Distribution （贝塔分布）

Beta函数

B(a,b)=\int_1^0x^{a-1}(1-x)^{b-1}dx,a>0,b>0

性质：

$(1.)\quad B(a,b)=B(b,a)$

$(2.)\quad B(a,b)=\frac{\Gamma(a)\Gamma(b)}{\Gamma(a+b)}$

Beta分布

p(x)= \begin{cases} \frac{1}{B(a,b)}x^{a-1}(1-x)^{b-1}, & 0<x<1 \\ 0, & \text{其他} & \end{cases}

关于概率分布的复习基本完了，对相关主题感兴趣的读者欢迎留言交流讨论。更多优质内容请欢迎扫码关注瑞行AI：